详解树状数组

news2024/11/18 18:28:18

前言

树状数组或二叉索引树（Binary Indexed Tree），又以其发明者命名为 Fenwick 树。其初衷是解决数据压缩里的累积频率的计算问题，现多用于高效计算数列的前缀和、区间和。它可以以 O(logn) 的时间得到任意前缀和。并同时支持在 O(logn) 时间内支持动态单点值的修改。空间复杂度 O(n)。

一、树状数组概括

树状数组是一个查询和修改复杂度都为log(n)的数据结构。主要用于数组的单点修改&&区间求和，另外一个拥有类似功能的是线段树。

具体区别和联系如下：

1.两者在复杂度上同级, 但是树状数组的常数明显优于线段树, 其编程复杂度也远小于线段树.

2.树状数组的作用被线段树完全涵盖, 凡是可以使用树状数组解决的问题, 使用线段树一定可以解决, 但是线段树能够解决的问题树状数组未必能够解决.

3. 树状数组的突出特点是其编程的极端简洁性, 使用lowbit技术可以在很短的几步操作中完成树状数组的核心操作，其代码效率远高于线段树。

二、树状数组的应用

1.单点修改+区间查询

代码示例

int lowbit(int x)
{
  return x & (-x);//表示求数组下标二进制的非0最低位所表示的值
}

//查找1~x的和
int find_sum(int x)
{
  int ans = 0;
  while(x)
  {
    ans += c[x];//从右往左累加求和
    x -= lowbit(x);
  }
  return x;
}

//单点修改
void gexi(int x,int v)
{
  a[x] += v;
  while(x <= n)
  {
    c[x] += v;
    x += lowbit(x);//由叶子节点向上更新树状数组C，从左往右更新
  }
}

实现原理

模板中最常见的三个函数：

①取数组下标二进制非0最低位所表示的值；

②单点更新；

③区间查询。

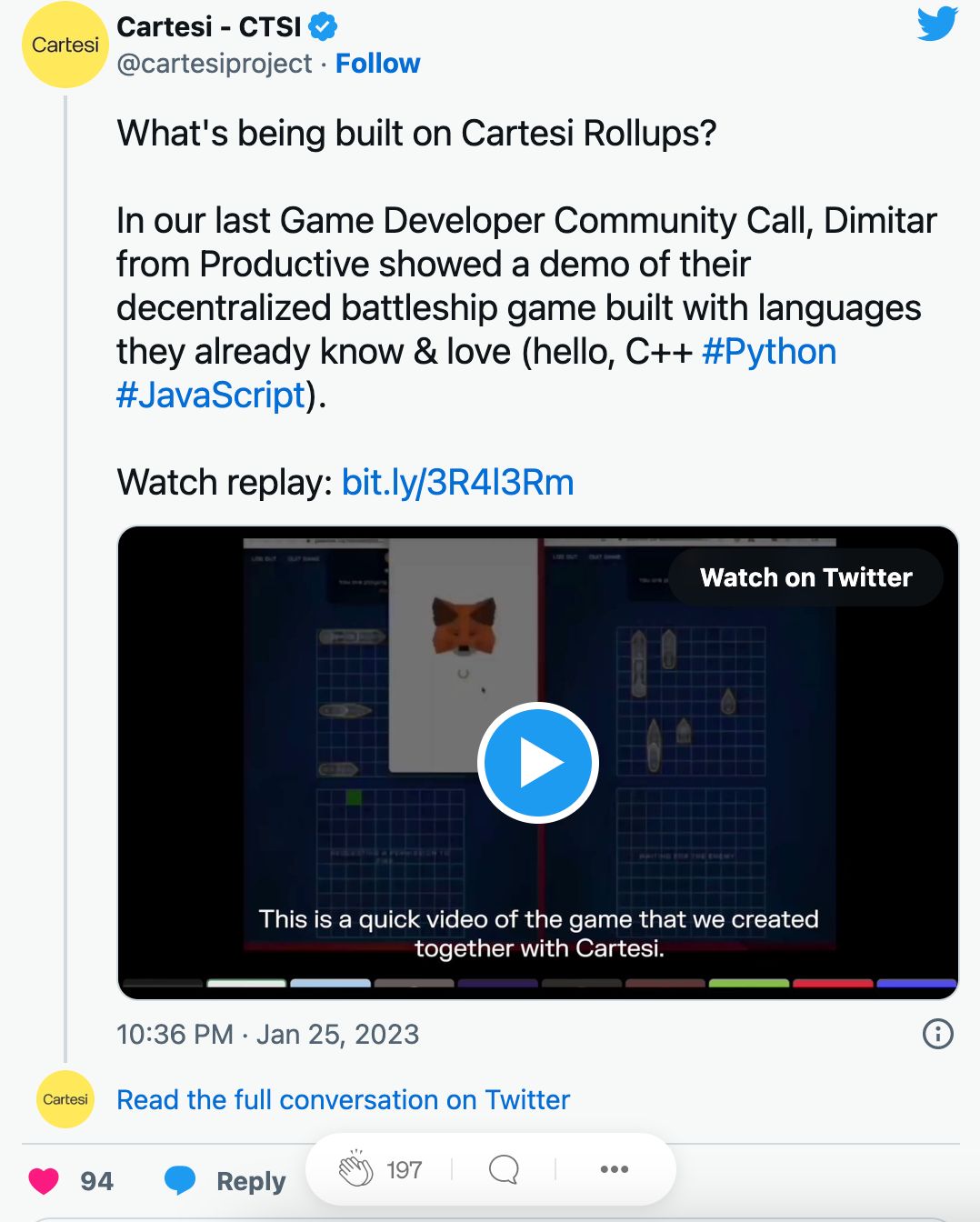
树状数组，顾名思义是树状的数组，我们首先引入二叉树，叶子节点代表A[1]~A[8]。

现在变形一下：

现在定义每一列的顶端节点C数组（其实C数组就是树状数组），如图：

理解树状数组的重点

C[i]代表子树的叶子节点的权值之和，如图可以知道：

C[1]=A[1];

C[2]=A[1]+A[2];

C[3]=A[3];

C[4]=A[1]+A[2]+A[3]+A[4];

C[5]=A[5];

C[6]=A[5]+A[6];

C[7]=A[7];

C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

首先是区间查询（求和）：

利用C[i]数组，求A数组中前i项和，举两个栗子：

①i=7

前7项和：sum[7]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]；

而C[4]=A[1]+A[2]+A[3]+A[4]；C[6]=A[5]+A[6]；C[7]=A[7]；

可以得到：sum[7]=C[4]+C[6]+C[7]。

数组下标写成二进制：sum[(111)]=C[(100)]+C[(110)]+C[(111)]；

②i=5

前5项和：sum[5]=A[1]+A[2]+A[3]+A[4]+A[5]；

而C[4]=A[1]+A[2]+A[3]+A[4]；C[5]=A[5]；

可以得到：sum[5]=C[4]+C[5]；

数组下标写成二进制：sum[(101)]=C[(100)]+C[(101)]；

细细观察二进制，树状数组追其根本就是二进制的应用，结合代码演示一下代码过程：

//查找1~x的和
int find_sum(int x)
{
  int ans = 0;
  while(x)
  {
    ans += c[x];
    x -= lowbit(x);
  }
  return x;
}

代码推演

对于i=7进行演示：

7(111)  ans+=C[7]

lowbit(7)=001 7-lowbit(7)=6(110) ans+=C[6]

lowbit(6)=010 6-lowbit(6)=4(100) ans+=C[4]

lowbit(4)=100 4-lowbit(4)=0(000) break；

对于i=5进行演示：

5(101)  ans+=C[5]

lowbit(5)=001 5-lowbit(5)=4(100) ans+=C[4]

lowbit(4)=100 4-lowbit(4)=0(000) break；

然后单点更新：

当我们修改A数组中某个值时，应当如何更新C数组呢？回想一下，区间查询的过程，再看一下上文中列出的过程。这里声明一下：单点更新实际上是不修改A数组的，而是修改树状数组C，向上更新区间长度为lowbit(i)所代表的节点的值。

//单点修改
void gexi(int x,int v)
{
  a[x] += v;
  while(x <= n)
  {
    c[x] += v;
    x += lowbit(x);
  }

如图：当在A[1]加上值val，即更新A[1]时，需要向上更新C[1],C[2],C[4],C[8]，这个时候只需将这4个节点每个节点的值加上val即可。这里为了方便大家理解，人为添加了个A数组表示每个叶子节点的值，事实上A数组并不用修改，实际运用中也可不设置A数组，单点更新只需修改树状数组C即可。下标写成二进制：C[(001)],C[(010)],C[(100)],C[(1000)]；

lowbit(1)=001 1+lowbit(1)=2(010) C[2]+=val；

lowbit(2)=010 2+lowbit(2)=4(100) C[4]+=val；

lowbit(4)=100 4+lowbit(4)=8(1000) C[8]+=val；

由于c[1] c[2] c[4] c[8] 都包含有A[1]，所以在更新A[1]时实际上就是更新每一个包含A[1]的节点。