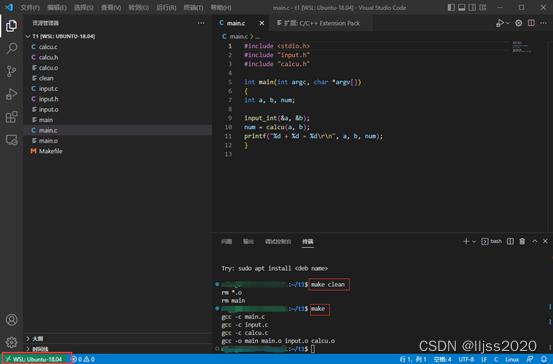
题目大意：

        n个数，共有n！种排列方式，记Pi(a)表示序列a的第i种排队方式，cnt(Pi(a))表示P(i)的逆序对个数，PLMM想知道这n！种排列方式共有多少对逆序对

        给定一个 nnn 个数，在所有排列顺序中，每种排列的分别的逆序对总数的总数是多少

思路：

        对于互不相等的两数 (a,b)，满足 a>b，显然 (a,b)成为逆序对，当且仅当a出现在b之前。所以我们注意到：在 n!次排列下，要么 a 在 b 前面，要么 b 在 a 前面，且两种情况出现的概率都为 1/2​。所以我们对于互不相同的一组 (a,b)，计算 (a,b) 的所有排列情况并乘上 1/2即可。

        具体如何计算(a,b)对答案的贡献呢？

        

1. 对于 a，在未确定位置的 n 个数中它的摆放可以是 n 种
2. 对于b，在未确定位置的n-1个数种它的摆放可以是n-1种
3. 所以a，b可以放置的总方案数位n*(n-1)，但是需要除以二，因为我们只要大数在前
4. 剩下的n-2个数，全排列即可(n-2)! 

      由于对于每一个不同的对，处理情况都是一样的，所以只需要统计出来有多少不同的对数，最终乘上一个(n)*(n-1)/2*(n-2)!即可

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+5,mod=1e9+7;

int n,w[N];
int f[N*2];

signed main() {
	f[1]=1;
	for(int i=2; i<=N; i++) {
		f[i]=f[i-1]*i%mod;
	}

	cin>>n;
	for(int i=1; i<=n; i++) {
		cin>>w[i];
	}

	sort(w+1,w+1+n);

	if(n==1) {
		cout<<0;
	} else {
		int cnt=0;//记录不同的对数
		for(int i=1; i<=n; i++) {
			int fid=lower_bound(w+1,w+1+n,w[i])-(w+1);//找到第一个大于等于它的数的下标(0------n-1)
			//找到的这个fid就是前面有多少个小于它的
			cnt+=fid;
		}

		int put=(n*(n-1)/2)%mod*f[n-2]%mod;
		//意思是，对于每个对，先找两个位置安排两个数，C(n,2)，但是我们只要
		//大数在前的情况，所以除2，另外的数随便安排，这样这个对对答案能贡献多少就算出来了
		//一个有cnt对，所以把所有对加起来就行了
		//因为每个对对答案的贡献是一样的
		//所以
		cout<<(cnt*put+mod)%mod;
	}
	return 0;
}