回溯算法-以学生就业管理系统为例

news2025/1/16 6:02:38

1.回溯算法介绍

1.来源

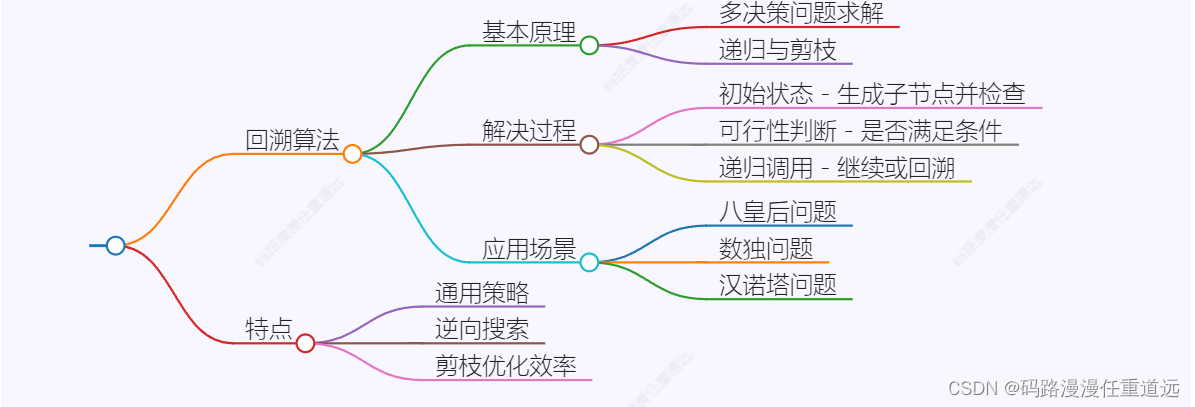
回溯算法也叫试探法，它是一种系统地搜索问题的解的方法。

用回溯算法解决问题的一般步骤：

1、针对所给问题，定义问题的解空间，它至少包含问题的一个（最优）解。

2 、确定易于搜索的解空间结构,使得能用回溯法方便地搜索整个解空间。

3 、以深度优先的方式搜索解空间，并且在搜索过程中用剪枝函数避免无效搜索。

确定了解空间的组织结构后，回溯法就从开始结点（根结点）出发，以深度优先的方式搜索整个解空间。这个开始结点就成为一个活结点，同时也成为当前的扩展结点。在当前的扩展结点处，搜索向纵深方向移至一个新结点。这个新结点就成为一个新的活结点，并成为当前扩展结点。如果在当前的扩展结点处不能再向纵深方向移动，则当前扩展结点就成为死结点。此时，应往回移动（回溯）至最近的一个活结点处，并使这个活结点成为当前的扩展结点。回溯法即以这种工作方式递归地在解空间中搜索，直至找到所要求的解或解空间中已没有活结点时为止。 [2]

2.基本思想

回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。八皇后问题就是回溯算法的典型，第一步按照顺序放一个皇后，然后第二步符合要求放第2个皇后，如果没有位置符合要求，那么就要改变第一个皇后的位置，重新放第2个皇后的位置，直到找到符合条件的位置就可以了。回溯在迷宫搜索中使用很常见，就是这条路走不通，然后返回前一个路口，继续下一条路。回溯算法说白了就是穷举法。不过回溯算法使用剪枝函数，剪去一些不可能到达最终状态（即答案状态）的节点，从而减少状态空间树节点的生成。回溯法是一个既带有系统性又带有跳跃性的的搜索算法。它在包含问题的所有解的解空间树中，按照深度优先的策略，从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时，总是先判断该结点是否肯定不包含问题的解。如果肯定不包含，则跳过对以该结点为根的子树的系统搜索，逐层向其祖先结点回溯。否则，进入该子树，继续按深度优先的策略进行搜索。回溯法在用来求问题的所有解时，要回溯到根，且根结点的所有子树都已被搜索遍才结束。而回溯法在用来求问题的任一解时，只要搜索到问题的一个解就可以结束。这种以深度优先的方式系统地搜索问题的解的算法称为回溯法，它适用于解一些组合数较大的问题。

2.代码介绍

// 主函数，用于启动就业组合生成过程
private static void generateAllPossibleEmploymentCombinations(GraduateService graduateService, JobService jobService) {
    // 获取所有毕业生和职位的列表
    List<Graduate> graduates = graduateService.listAllGraduates();
    List<Job> jobs = jobService.listAllJobs();

    // 存储所有可能的就业组合的列表
    List<List<Employment>> allCombinations = new ArrayList<>();
    // 调用递归函数生成组合，限制为100条
    generateCombinations(graduates, jobs, new ArrayList<>(), allCombinations, 0, 100);

    // 打印所有可能的就业组合（数据量过大时只显示前100条）
    int combinationNumber = 1; // 组合计数器
    for (List<Employment> combination : allCombinations) {
        // 跳过空组合
        if (combination.isEmpty()) continue;
        // 打印非空组合及其序号
        System.out.println("组合 " + combinationNumber++ + "：" + combination);
    }
}

/**
 * 递归函数，用于生成就业组合。
 * 运用了回溯算法，通过递归探索所有可能的毕业生与职位的匹配。
 */
private static void generateCombinations(List<Graduate> graduates, List<Job> jobs, 
                                          List<Employment> currentCombination, 
                                          List<List<Employment>> allCombinations, 
                                          int start, int limit) {
    // 如果已经达到组合数量限制，则停止递归
    if (allCombinations.size() >= limit) {
        return;
    }

    // 只有在当前组合非空时才添加到所有组合列表中
    if (!currentCombination.isEmpty()) {
        allCombinations.add(new ArrayList<>(currentCombination));
    }

    // 双重循环遍历所有毕业生和职位
    for (int i = start; i < graduates.size(); i++) {
        Graduate graduate = graduates.get(i);
        for (Job job : jobs) {
            // 检查毕业生是否适合职位
            if (isSuitable(graduate, job)) {
                // 创建就业对象并添加到当前组合
                Employment employment = new Employment(graduate.getStudentId(), job.getJobId());
                currentCombination.add(employment);
                // 递归调用，继续添加下一个毕业生和职位的组合
                generateCombinations(graduates, jobs, currentCombination, allCombinations, i + 1, limit);
                // 回溯，移除当前就业对象，恢复到上一个状态
                currentCombination.remove(currentCombination.size() - 1);
            }
        }
    }
}

// 检查毕业生是否适合职位的函数，这里简化为所有毕业生适合所有职位
private static boolean isSuitable(Graduate graduate, Job job) {
    return true;
}