前言

（关于代码实现的图结构，可以看图结构的实现这篇文章）

Dijkstra的实现与Prim的实现相似，两者都是通过贪心思想实现，它们有什么不同呢？首先Prim算法是针对无向图的最小生成树的，而Dijkstra算法是针对有向图的最短路径生成。一个的目的是连接图中的所有顶点，生成一个连通图，一个的目的是连接图中的两个顶点，两顶点之间的最短路径嘛，只要连接两个顶点即可，只是这个过程中可能会连接其他顶点，连接了n个顶点中的n-2个，也就把所有顶点连接了。为什么说这两个算法相似呢？以下是我的个人见解

Dijkstra算法讲解与实现

首先Dijkstra的思想是贪心，既然要求最短路径，我们肯定要知道求的是哪两个顶点间的最短路径吧？所以Dijkstra会接收一个顶点值，将其作为起点，找出该点与其他所有顶点之间的最短路径，那么这个最短指的是什么呢？它是指路径上的所有边的权值相加之和最小，并且这里假设没有负权值。

Dijkstra以调用者传入的顶点为起点，将已确定最短路径的顶点放入一个集合，我们用bool数组保存顶点的最短路径是否被确定的标记，确定了的顶点被标记为true。接着我们还需要两个数组，一个是距离数组，记录该顶点到其他顶点的最短距离，一个是父顶点数组，记录每个顶点的父顶点（比如8->6->9这个路径中，9的父顶点是6），用顶点的父顶点不断地迭代就能得到该顶点与起点之间的最短路径，这两个数组都是函数的输出型参数。随着已确定最短路径集合的不断扩大，最短路径的创建也随着完成，那么现在的问题是已确定最短路径集合要怎么扩大，换句话说要怎么确定起点到某顶点的最短路径？这个过程分为两步，一是更新起点到未确定最短路径顶点间的距离，二是从中选择一个最小距离，将该顶点加入已确定最短路径顶点集合中。由于新顶点的加入，我们可以选择的边变多了，此时顶点到未确定最短路径顶点间的距离也发生变化，所以我们要重复上面的步骤，更新这些距离，然后选择最小的，再更新…说的有些抽象，通过一个具体的例子解释一下

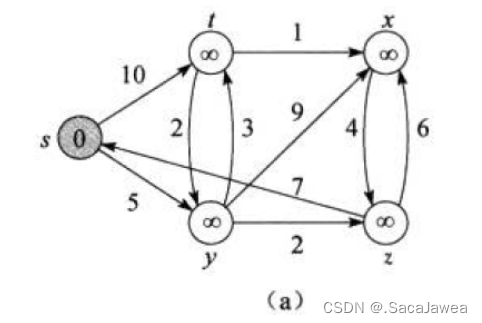
（用来讲解的图片都来自《算法导论》）顶点中的数字表示该顶点与起点间的最短距离，这也是我们要更新的距离数组。比如将s顶点作为Dijkstra的起点，s就是起点，所以它到起点的距离为0（图片上表示0，此时我们要更新距离数组），距离数组的其他成员被更新成最大值（图片用无穷符号表示），并且父顶点数组中，起点位置保存的是起点的下标，其他位置初始化为-1。这是构建最短路径前的初始化工作，现在开始重复刚才说的步骤，由于已确定最短路径集合中加入了新的顶点（起点），所以我们需要更新起点与未确定最短路径集合中顶点的距离，这里就遍历邻接矩阵/邻接表，查找与新加入的顶点相连的边，注意这些边的终点需要指向未确定的集合中，如果指向已确定集合中不就构成了环路或者重复路径了吗？更新的依据是：查找距离数组，如果顶点到这条边的起点（肯定是处于已确定集合中的顶点） 的最短距离+这条边的权值，小于距离数组中该顶点的值，才需要更新距离数组。我们默认距离数组中保存的是起点与某顶点间的最短距离，当计算出一个小于“最短距离”的值时，我们当然需要替换这个最短距离。因为距离数组都是用权值的最大值初始化的，所以大概率这些“最短距离”会被更新。看上面的例子，由于已确定集合中加入了新的顶点（起点s），所以我们遍历邻接矩阵，发现连接s的边有s->y，s->t两条，由于这两条边的权值+起点到这两条边的父顶点的最短路径（起点到起点距离为0）小于距离数组中保存的值，所以我们更新距离数组，直观的变化如下入所示

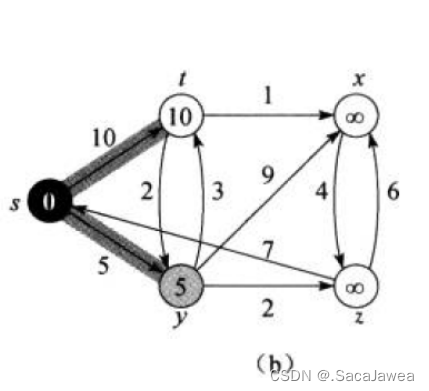
我们将：由于已确定最短路径集合中新顶点的加入而更新距离数组的操作叫做松弛，一开始，起点就是加入的已确定集合的新顶点，此时我们对起点进行松弛操作，更新了两个距离，s->y，s->t。这是第一步，第二步就是从距离数组中查找最小的距离，此时选择权值最小的那条边，将边的终点加入以确定集合。可能有人就会问了，为什么此时可以确定出最短路径？首先距离数组保存了什么？当前起点到某顶点间的最短距离，在已确定集合不加入新顶点的情况下，这些距离是不会发生改变的，从当前的最短距离中选择一个最小的，这是不是一个局部的最优选择？这样选择的原因也是由于贪心思想的指导，局部最优嘛，那这里局部最优为什么不会出错呢？记得我最开始做的一个假设：所有权值中没有负权值，也就是说随着边的不断增加，总权值也是不断增加的，不在当前选择最小的，难道是想要从全局出发找一条比现在更短的路径？由于权值只会不断增加，所以当前的就是最好的。因此我们选择了s->y这条边，将y放入已确定集合中，而s->t的距离呢，它可以再小吗？当然了，我们从s->y这条边出发，绕个路，说不定就有一条更短的路径，所以t不能加入已确定集合，我们每次只能选择路径最短的顶点。那么总结一下，构建最短路径的过程分为顶点的松弛+最短路径的选择，两步，由于最短路径的选择将为已确定集合带来新顶点，所以我们又需要进行顶点的松弛+再次的最短路径选择，这样不断重复，重复一次就确定一条最短路径，直到所有的最短路径被确定，Dijkstra算法完成。

由于Dijkstra较为抽象，这里继续上面的例子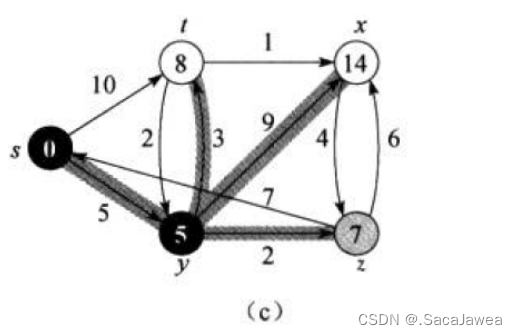
将y加入已确定集合中对y进行松弛操作，更新起点到未确定顶点的距离
s->t被更新为8，s->z被更新为7，s->x被更新为14。你看s->t的距离被更新成更短的了，此时我们再从距离数组中选择一个最小的顶点，s->z最小，所以z加入已确定集合，再对z进行松弛操作…

这里与Prim进行对比，Prim算法也将所有顶点分为两个集合，已连接的顶点和未连接的顶点，每次新顶点加入已连接集合时，Prim也要进行更新，只不过Prim是用优先级队列维护数据，Dijkstra是用距离数组进行数据维护。两者的区别是什么呢？Prim只需要根据新的可以选择的边更新优先级队列，注意Prim只关注边的权值，所以每次选择的边都是权值最小的边，而Dijkstra呢？虽然也是根据新的可以选择的边更新距离数组，但Dijkstra关注的不只是边的权值，还关注起点到边的父顶点间的权值，换句话说就是起点到某顶点间的最短距离，这不只是Prim关注的边的权值那么简单，Dijkstra还需要考虑起点到边的父顶点的距离，当然这个距离是已经确定的最短距离（因为父顶点处于已确定最短路径的集合中）。由于已确定最短距离的顶点集合会发生变化，起点到某一顶点的距离也会发生变化，这样的不断变化就使得每次加入新的顶点就要进行一次距离的维护（判断新的距离是否比之前的更短），这也使得最短距离的维护不适合用优先级队列，我们每次都要遍历距离数组进行O(n)的查找才能得到最小的距离。它们两的区别，怎么说呢，两者的实现都是相似的，就是需要维护的数据不同，并且Dijkstra维护的数据还会变化，所以Dijkstra有了一个松弛操作。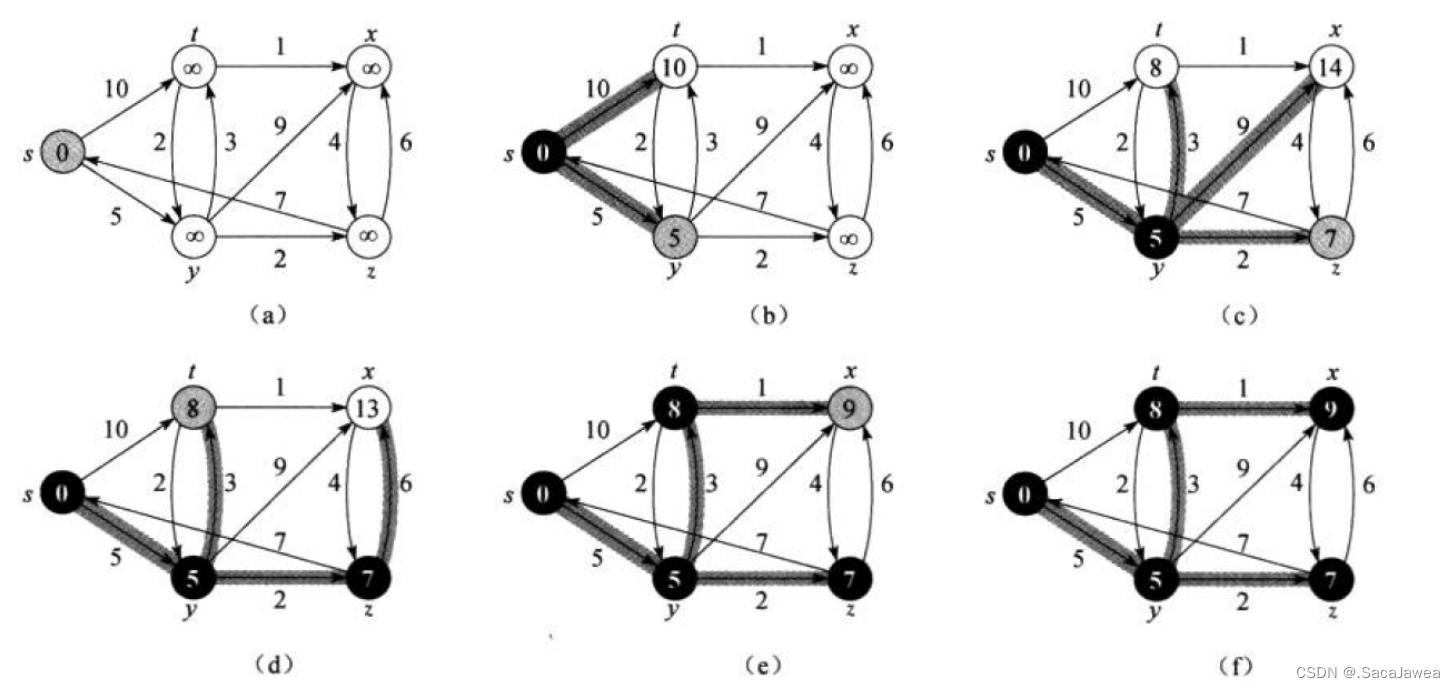
对于讲解的例子，这里给出完整的路径构建过程，只要记住：松弛+选择最短，这两个关键词就行了，Dijkstra就是这两个步骤的不断重复，只是需要一个初始化工作，将起点加入已确定集合，所以第一步的松弛是对起点进行的。下面给出具体的代码实现

// 接收顶点，输出型参数距离数组与父顶点数组
void Dijkstra(const V& start, vector<W>& dist, vector<size_t>& parent)
{
	// 将起点转换成下标
	size_t starti = get_index(start);
	if (starti == -1)
	{
		throw invalid_argument("起点不存在");
	}

	// 顶点个数的记录
	size_t vertex_size = _vertex.size();
	// 最大值初始化距离数组
	dist.resize(vertex_size, MAX_W);
	// 用-1初始化父顶点数组
	parent.resize(vertex_size, -1);
	// 标记数组的建立与初始化
	vector<bool> vertex_had(vertex_size, false);

	// 三个数组的初始化
	dist[starti] = W();
	parent[starti] = starti;
	vertex_had[starti] = true;
	// 至此初始化工作完成

	// 新加入已确定集合的下标记录
	size_t new_joini = starti;
	// 循环遍历的创建
	size_t finish = 0;
	// vertex_size个顶点要构建vertex_size-1条最短路径
	while (finish != vertex_size - 1)
	{
		// 对新加入的顶点进行松弛操作
		for (size_t desti = 0; desti < vertex_size; ++desti)
		{
			// 需要判断的是这条边是否存在
			// 这条边的终点是否在已确定集合中
			// 起点到这条边的父顶点的最短距离+这条边的权值是否小于原来记录的最短距离
			if (_matrix[new_joini][desti] != MAX_W
				&& vertex_had[desti] == false
				&& _matrix[new_joini][desti] + dist[new_joini] < dist[desti])
			{
				// 距离数组的更新
				dist[desti] = _matrix[new_joini][desti] + dist[new_joini];
				// 父顶点数组的更新
				parent[desti] = new_joini;
			}
		}

		//  松弛完成，选择距离数组中最小的一个路径
		W min_w = MAX_W;
		for (size_t i = 0; i < vertex_size; ++i)
		{
			// 找最小，注意选择的边的终点必须在未确定集合中
			if (vertex_had[i] == false && dist[i] < min_w)
			{
				min_w = dist[i];
				// 确定的最短路径的顶点下标维护
				new_joini = i;
			}
		}
		// 选出了最短路径后，标记数组的更新
		vertex_had[new_joini] = true;
		// 循环变量的维护
		finish++;
	}
}

// for test
void print_det(const V& start, vector<W>& dist, vector<size_t>& parent)
{
	// 将起点转换成下标
	size_t starti = get_index(start);
	if (starti == -1)
	{
		throw invalid_argument("起点不存在");
	}
	
	string str;
	for (size_t i = 0; i < parent.size(); ++i)
	{
		size_t cur = i;
		while (cur != starti)
		{
			str += _vertex[cur];
			cur = parent[cur];
		}
		reverse(str.begin(), str.end());
		cout << _vertex[starti];
		for (size_t j = 0; j < str.size(); ++j)
		{
			cout << "->" << str[j];
		}
		cout << ':' << dist[i] << endl;
		str.clear();
	}
}

由于实现算法之前已经讲解了大概的逻辑，并且代码也给出了详细的注释，这里就不再赘述，直接进行程序的测试

#include "Graph.hpp"
#include "UnionFindset.hpp"

int main()
{
	matrix::graph<char, int, INT_MAX, true> g;

	g.add_tex('x');
	g.add_tex('y');
	g.add_tex('z');
	g.add_tex('s');
	g.add_tex('t');

	g.add_edge('s', 't', 10);
	g.add_edge('s', 'y', 5);
	g.add_edge('y', 't', 3);
	g.add_edge('y', 'x', 9);
	g.add_edge('y', 'z', 2);
	g.add_edge('z', 's', 7);
	g.add_edge('z', 'x', 6);
	g.add_edge('t', 'y', 2);
	g.add_edge('t', 'x', 1);
	g.add_edge('x', 'z', 4);

	vector<int> dist;
	vector<size_t> parent;
	g.Dijkstra('s', dist, parent);
	g.print_det('s', dist, parent);
	
	return 0;
}

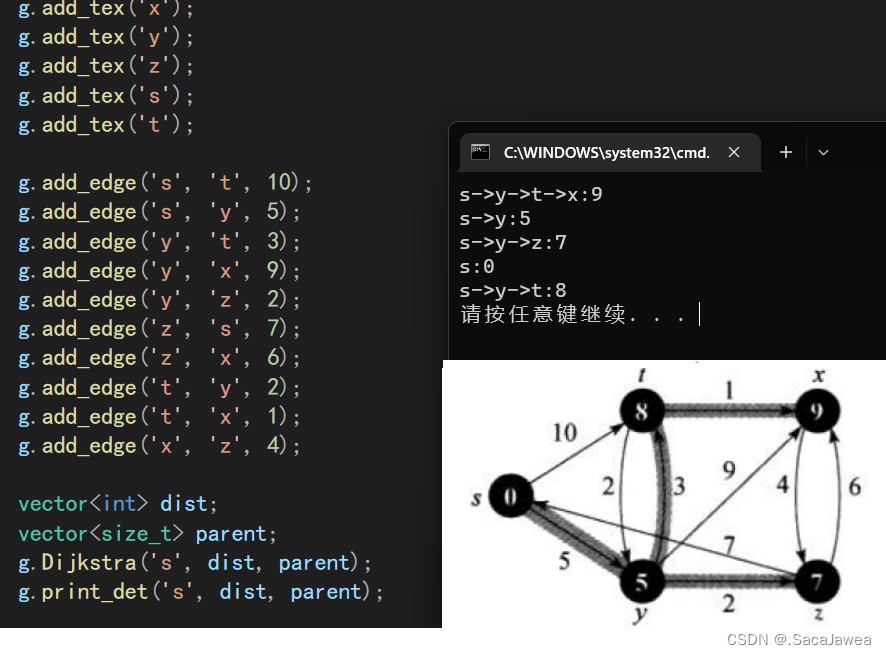
至此，Dijkstra算法讲解与实现完成

Bellman Ford算法与实现

Bellman Ford算法呢，也是求解最短路径问题的。对于Dijkstra算法，Bellman Ford算法主要使用在含有负权值的图中，在讲解Dijkstra时，我一开始就强调了：假设所有权值中没有负权值，为什么要这样假设？因为只有这样我们才能进行贪心，也就是说随着路径中边的数量增加，权值只会不断的增加，根据这个结论我们才确定每次选择的路径是最短的。像上面的例子，一开始s->y的权值是5，s->t的权值是10，为什么我们就能确定s->y的最短路径是s->y？因为从s->t走，绕路走到y顶点，权值之和势必会比10大，但如果权值中存在负权值呢？可能t->y的权值是-8，这样的话s->t->y
的权值就是2，比s->y的权值5小，那么我们选择s->y为s顶点到y顶点的最短路径就是错误的。因此在含有负权值的图中，我们不能直接用贪心，局部最优的方式确定两点的最短路径，我们只能通过不断地遍历所有边，穷尽到一个顶点的所有路径，最后得到一条最短的。这也是我们常说的暴力求解，说白了Bellman Ford就是暴力

讲解Dijkstra时，我提到了一个操作：松弛，每进行一次循环，已确定集合就会增加一个顶点，我们就需要对这个顶点进行松弛操作，来更新距离数组。但对于Bellman Ford，最短路径无法提前确定，所以更不存在什么已确定集合，但是我们可以假设最短路径被确定了，或者说两点之间可能才能在更短的路径，我们对所有顶点进行松弛操作，看更短的路径是否存在

而这样的松弛操作是建立在初始化距离数组的条件上，一开始距离数组被初始化为权值的最大值，也就是所有顶点到起点的距离都是最大值，在两者是连通的情况下，这肯定不是最短距离吧，所以此时对起点进行松弛操作，极大概率会改变距离数组，也就是从起点都某些顶点的距离缩小了，对于距离缩小的某些顶点，我们再进行松弛操作，此时又会有某些顶点的路径缩小，对这些顶点再进行松弛…直到没有顶点的路径缩小，此时最短路径构建完成，我们暴力的找出了起点到所有顶点的最短路径。

// 如果存在负权值环路，最短路径无解返回false
bool Bellman_Ford(const V& start, vector<W>& dist, vector<size_t>& parent)
{
	// 将起点转换成下标
	size_t starti = get_index(start);
	if (starti == -1)
	{
		throw invalid_argument("起点不存在");
	}

	// 顶点个数的记录
	size_t vertex_size = _vertex.size();
	// 最大值初始化距离数组
	dist.resize(vertex_size, MAX_W);
	// 用-1初始化父顶点数组
	parent.resize(vertex_size, -1);
	// 更新队列的创建 
	queue<size_t> update_queue;

	// 数组的初始化
	dist[starti] = W();
	parent[starti] = starti;
	// 将起点入队
	update_queue.push(starti);
	// 至此初始化工作完成

	while (!update_queue.empty())
	{
		// 得到要进行松弛的顶点下标
		size_t curi = update_queue.front();
		update_queue.pop();

		for (size_t desti = 0; desti < vertex_size; ++desti)
		{
			// 需要判断边是否存在
			// 现在的最短距离是否小于之前的最短距离
			if (_matrix[curi][desti] != MAX_W
				&& dist[curi] + _matrix[curi][desti] < dist[desti])
				// 如果满足条件，更新距离数组和父顶点数组
				// 并将该顶点下标入队，需要再次进行松弛操作
			{
				// 但需要注意的是不要构成负权值环路
				// 比如7->8->9，如果9要连接的是7，那么9的父顶点的父顶点和要连接的顶点下标相等
				// 判断当前顶点的父顶点的父顶点是否存在，
				// 如果存在且对于该顶点要连接的目标点，构成环路，返回false
				if (parent[curi] != -1 && parent[parent[curi]] == desti)
				{
					return false;
				}
				// 更新距离数组和父顶点数组
				dist[desti] = dist[curi] + _matrix[curi][desti];
				parent[desti] = curi;
				// 将该顶点下标入队
				update_queue.push(desti);
			}
		}
	}
	return true;
}

由于实现算法之前已经讲解了大概的逻辑，并且代码也给出了详细的注释，这里就不再赘述，直接进行程序的测试

int main()
{
	matrix::graph<char, int, INT_MAX, true> g;

	g.add_tex('x');
	g.add_tex('y');
	g.add_tex('z');
	g.add_tex('s');
	g.add_tex('t');

	g.add_edge('s', 't', 6);
	g.add_edge('s', 'y', 7);
	g.add_edge('y', 'z', 9);
	g.add_edge('y', 'x', -3);
	g.add_edge('z', 's', 2);
	g.add_edge('z', 'x', 7);
	g.add_edge('t', 'x', 5);
	g.add_edge('t', 'y', 8);
	g.add_edge('t', 'z', -4);
	g.add_edge('x', 't', -2);

	vector<int> dist;
	vector<size_t> parent;

	if (g.Bellman_Ford('s', dist, parent))
	{
		g.print_det('s', dist, parent);
	}
	else
	{
		cout << "存在负权回路" << endl;
	}
	
	return 0;
}

测试程序使用的例子与下图相同，《算法导论》也给出了使用Bellman Ford算法求得的正确答案，读者可以带入程序理解该算法求解的过程。

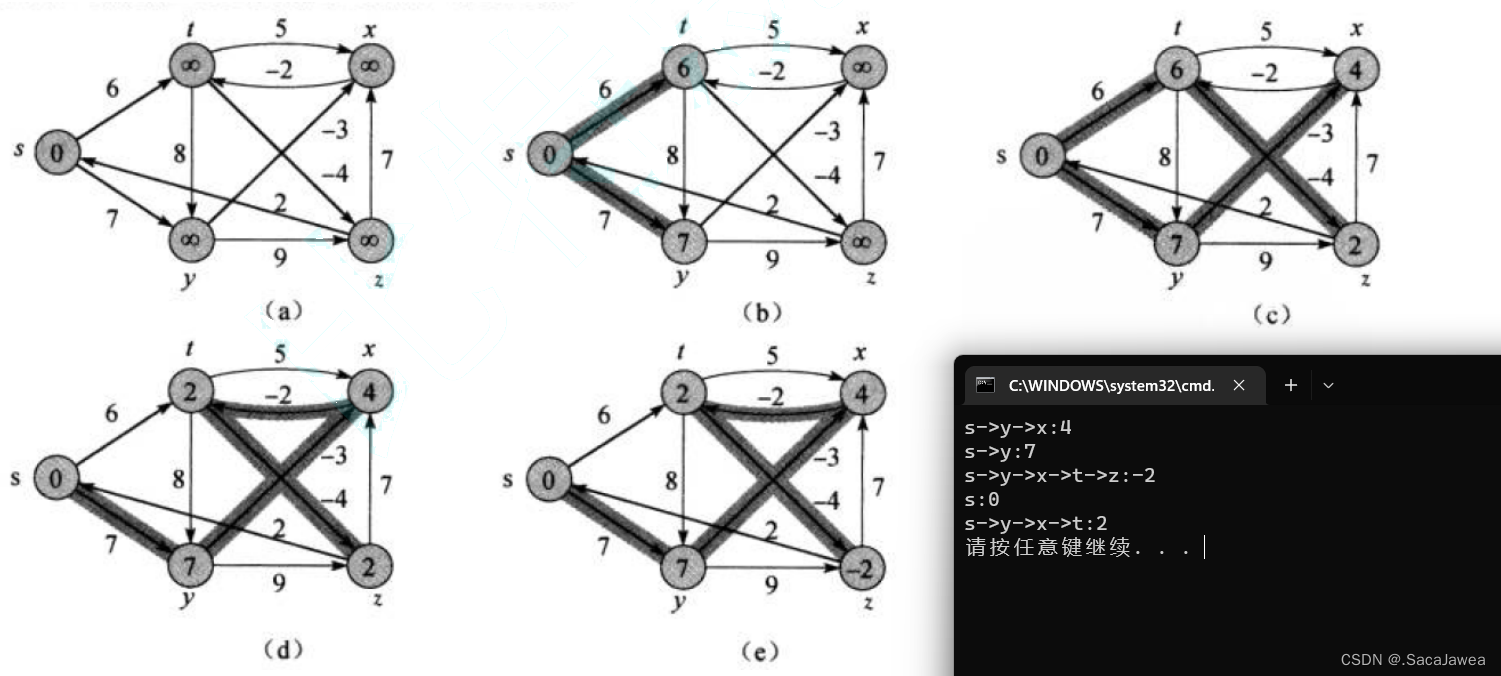
修改测试程序，创建一个带有负权值环路的图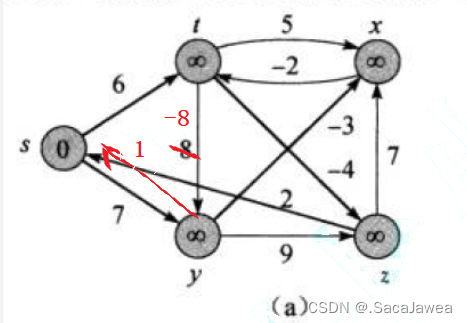
s->t->y->s形成一个负权值的环，也就是说只要一个走这个环，权值的总和就会一直减少，一直走，一直少，那么最短路径要如何求解？只要不断走这个环，起点到所有顶点的距离都是最小值，所以说带有负权值环路的图无法求解最短距离，这没有意义

int main()
{
	matrix::graph<char, int, INT_MAX, true> g;

	g.add_tex('x');
	g.add_tex('y');
	g.add_tex('z');
	g.add_tex('s');
	g.add_tex('t');

	g.add_edge('s', 't', 6);
	g.add_edge('s', 'y', 7);
	g.add_edge('y', 'x', -3);
	g.add_edge('y', 'z', 9);
	g.add_edge('y', 'x', -3);
	g.add_edge('y', 's', 1); // 新增
	g.add_edge('z', 's', 2);
	g.add_edge('z', 'x', 7);
	g.add_edge('t', 'x', 5);
	g.add_edge('t', 'y', -8); // 更改
	g.add_edge('t', 'z', -4);
	g.add_edge('x', 't', -2);
	vector<int> dist;
	vector<size_t> parent;

	if (g.Bellman_Ford('s', dist, parent))
	{
		g.print_det('s', dist, parent);
	}
	else
	{
		cout << "存在负权回路" << endl;
	}
	
	return 0;
}

那么经过了测试，Bellman Ford算法实现完成