二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

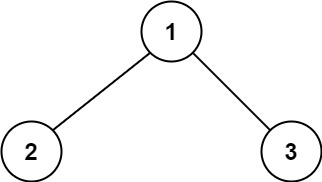
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

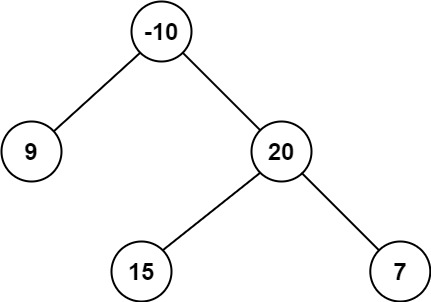
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

解决思路

找最大路径和本质是递归寻找当前节点最大路径

设置全局变量max

        在当前节点左边路径最大值加右边路径最大值大于max，赋值给max

        若小于max，就返回一条路径，左/右路径加当前节点值

        若左/右路径值小于0，那就舍弃，只取当前节点值

所以这个问题解决思路在于找当前节点最大值

        int L = Math.max(0, dfs(root.left));        //左路径若小于0，干脆不要了

        int R = Math.max(0, dfs(root.right));     //右路径同理

        max = Math.max(max, root.val + L + R);         //查询左路径加右路径加当前节点值

 解决

依照上述思路写出以下代码

class Solution {  
    // 定义一个全局变量来存储最大路径和  
    int max = Integer.MIN_VALUE;  
  
    // 主函数，用于启动深度优先搜索并返回最大路径和  
    public int maxPathSum(TreeNode root) {  
        dfs(root); // 从根节点开始深度优先搜索  
        return max; // 返回找到的最大路径和  
    }  
  
    // 深度优先搜索的辅助函数  
    // 该函数返回以当前节点为根的子树中，通过当前节点的最大单边路径和（不包括父节点）  
    int dfs(TreeNode root) {  
        if (root == null) {  
            // 如果当前节点为空，则返回0，表示没有路径和  
            return 0;  
        }  
  
        // 递归地计算左子树和右子树通过各自根节点的最大单边路径和（不包含当前节点）  
        // 注意这里使用Math.max(0, ...)来确保如果子树路径和为负，则忽略该子树  
        int L = Math.max(0, dfs(root.left));  
        int R = Math.max(0, dfs(root.right));  
  
        // 更新全局的最大路径和，考虑当前节点加上左右子树的最大单边路径和  
        max = Math.max(max, root.val + L + R);  
  
        // 返回以当前节点为根的子树中，通过当前节点的最大单边路径和  
        // 这里选择左子树或右子树中较大的一个加上当前节点的值  
        // 注意这里不考虑同时包含左右子树的情况，因为题目要求的是最大单边路径和  
        return Math.max(root.val + L, root.val + R);  
    }   
}