1. 概述

        矩阵式键盘由于有其占用硬件资源少的优点有着极其广泛的应用，如PC键盘、电话按键、家用电器等等这类产品.矩阵键盘的基本原理如下所示（仅是原理示例，实际实现上还会为每个按键加上防倒流的二极管解决“鬼影”问题），一般的实现上将每一行和每一列都连接到一个独立的IO上，对行和列进行独立扫描就可以知道那个按键被按下了。

        虽然采用矩阵式键盘可以降低硬件IO的数量，但对于要实现相同数量按键的矩阵键盘最少需要多少个IO驱动呢？需要硬件IO最小其实就是需要满足约束条件的最小值。

        上述约束条件实际上式还存在一些不严谨的地方，这里还有一个隐含条件x、y都需要是整数离散值，若需要实现按键数量n为质数，找到的x,y并不能使x+y值最小（如需要实现按键数量为17，只能找到x=1、y=17使得x+y=18个IO；其实5+4的IO数量就可以实现17个按键），若考虑x、y的整数取值，约束条件应该修改为:

        当为了简单起见，这里仍然使用约束条件，并假定x、y并不一定为整数，再找到x、y后在找到整数的x、y。

2. 何角度

从几何角度看待这个，x*y其实是矩形面积，x+y为矩阵的半周长，如下：

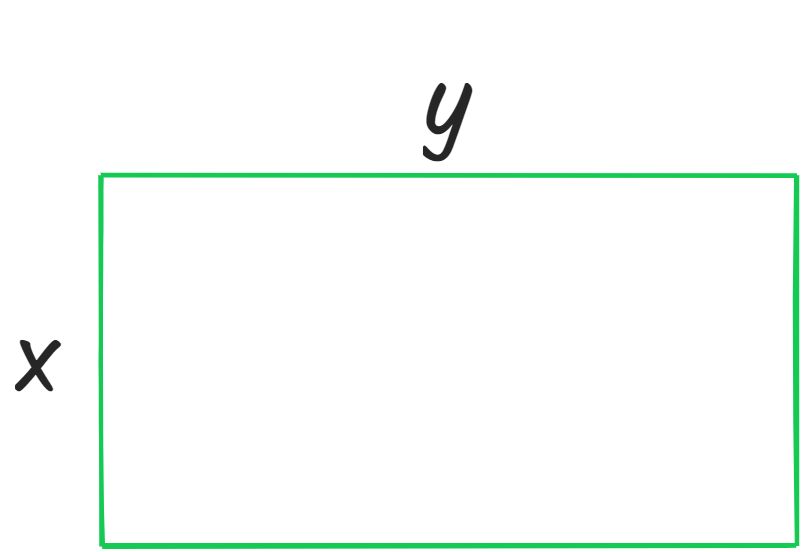
        这时我们就将求x+y的最小值转换成求在面积一定是求周长（半周长）的最小值，直接寻找x+y最小值仍然存在一定的难度，但我们可以反过来考虑，即在周长（a+b）一定情况下，怎么分配a、b长度使得这个矩形面积最大，这个问题就相对比较容易了：当a=b时矩形变成正方形，此时矩形的面积最大周长最短。

3. 微积分角度

        另外也可以从微积分的角度进行分析，首先

        对y进行代换后：

        f(x)的函数图像大概如下（下图将n取值100进行函数图像绘制）：

        通过函数图像，大概知道f(x)存在一个最小值，这个f(x)的最小值也是这个f(x)的极值点，对f(x)求导等于0的点为极值点：

        当的结果为整数时x+y的最小值为，当的结果不为整数时，x,y需要选择接近的整数且需要保证。

4. 算术-几何平均不等式

        上述无论是面积还是微积分角度都要求x,y为连续值，若为离散的整数，这时x、y需要满足以下等式：

        这里要要计算x+y的最小值就需要借助数学里面的一个重要的不等式 - 算术-几何平均不等式，对两个正实数存在以下不等式：

        将x于y的约束条件带入上式：

        通过算数-几何不等式可求的x+y的最小值为，由于x和y为整数需要对其结果做向上取整。