目录
一.安装grafana并启动
二.浏览器访问
三.导入zabbix数据,对接grafana
四.如何导入模版
以前两篇博客为基础
【分布式系统】监控平台Zabbix介绍与部署(命令+截图版)-CSDN博客
【分布式系统】监控平台Zabbix自定义模版配置-CSDN博客
一.安装grafana并启动
添加一台服务器192.168.80.104
初始化操作
systemctl disable --now firewalld
setenforce 0
vim /etc/selinux/config
SELINUX=disabledcd /opt
grafana-enterprise-9.4.7-1.x86_64.rpm #上传软件包
yum localinstall -y grafana-enterprise-9.4.7-1.x86_64.rpm #安装
systemctl enable --now grafana-server.service #开启服务
netstat -lntp | grep 3000 #查询是否已经开启服务

二.浏览器访问
浏览器输入http://192.168.80.104:3000
账号/密码:admin / admin
安装启动zabbix
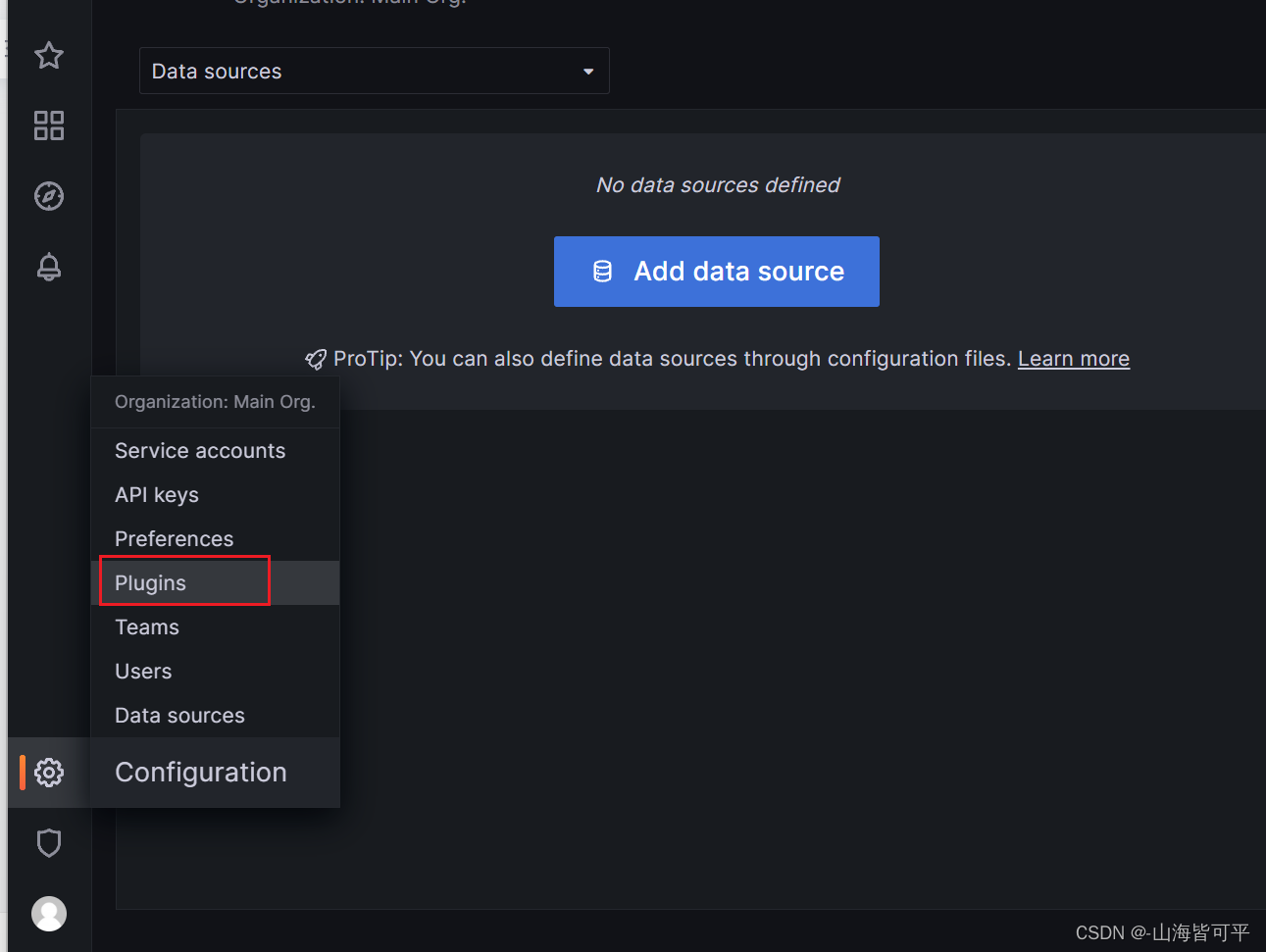
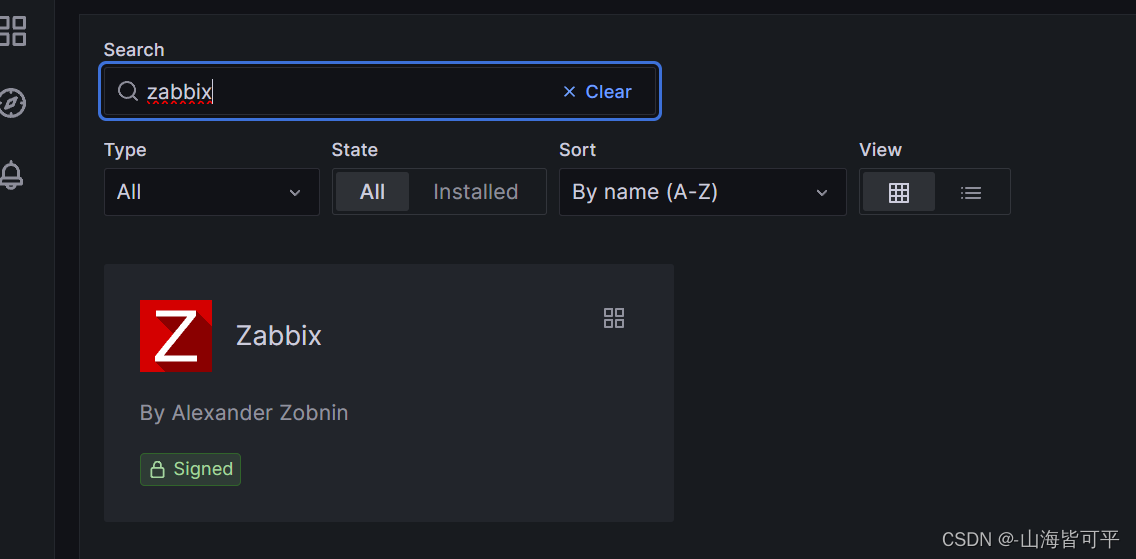
三.导入zabbix数据,对接grafana
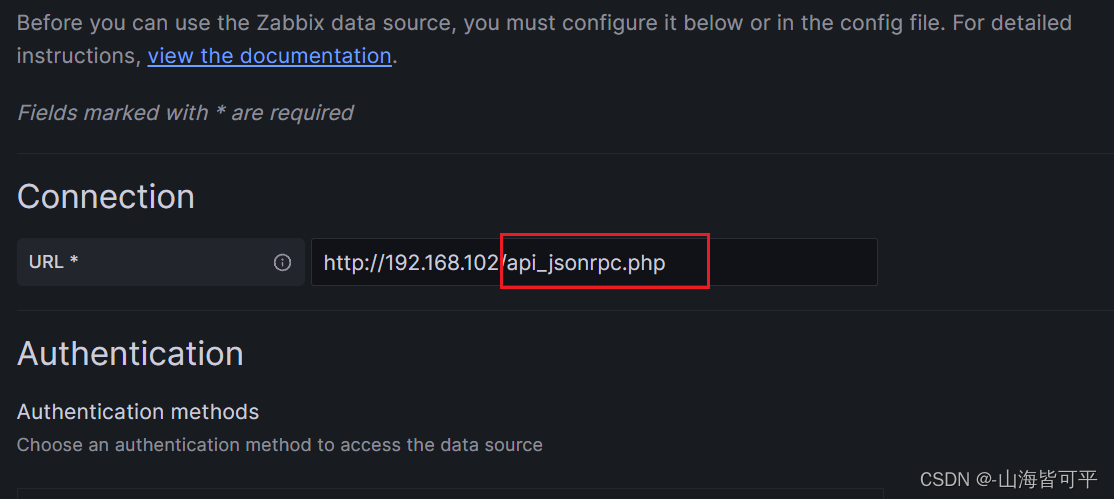
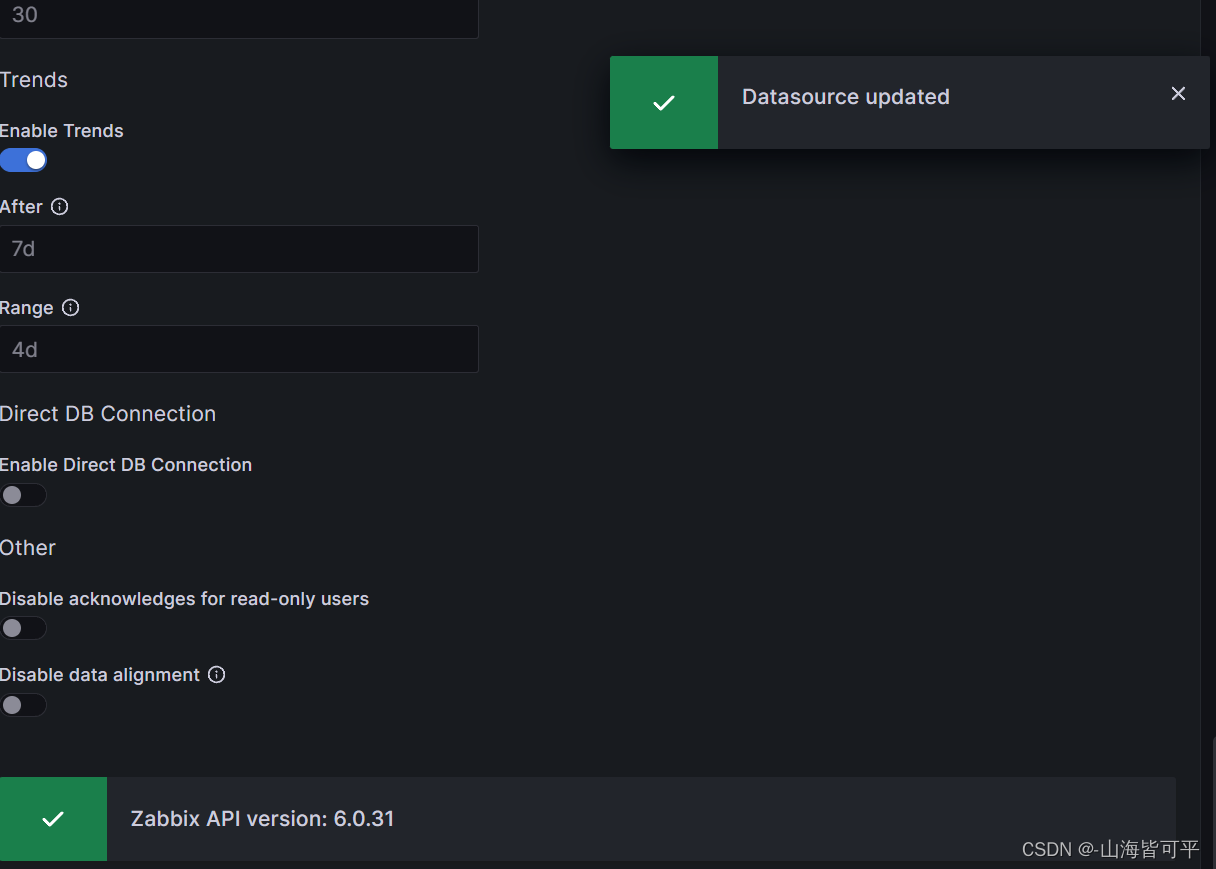
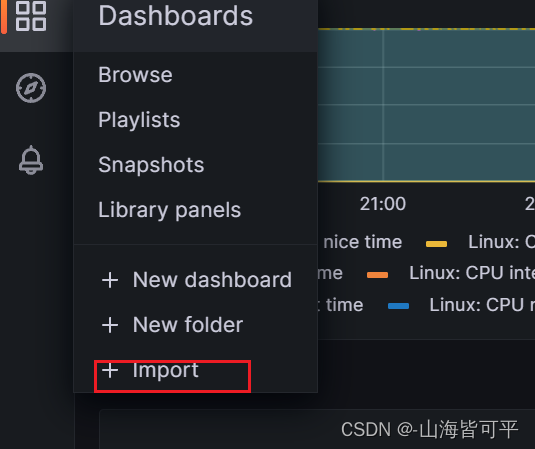
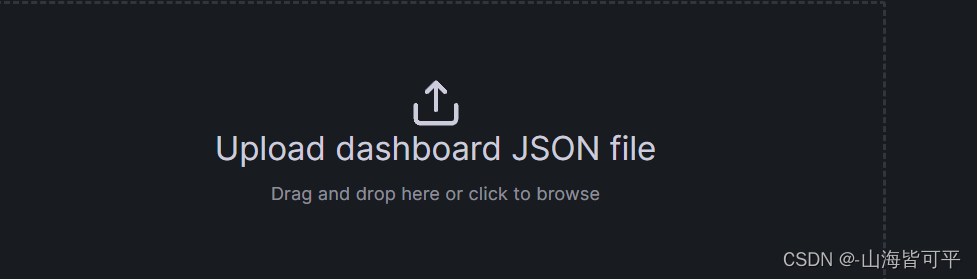
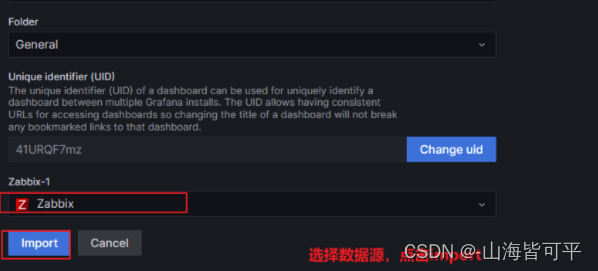
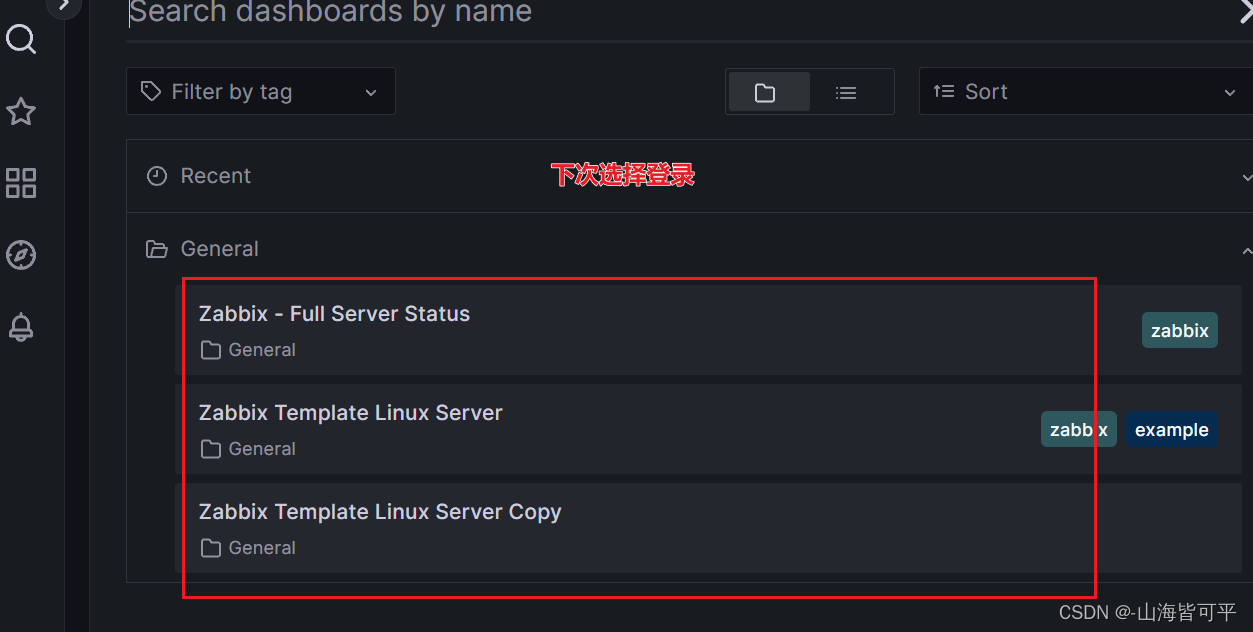
导入模版
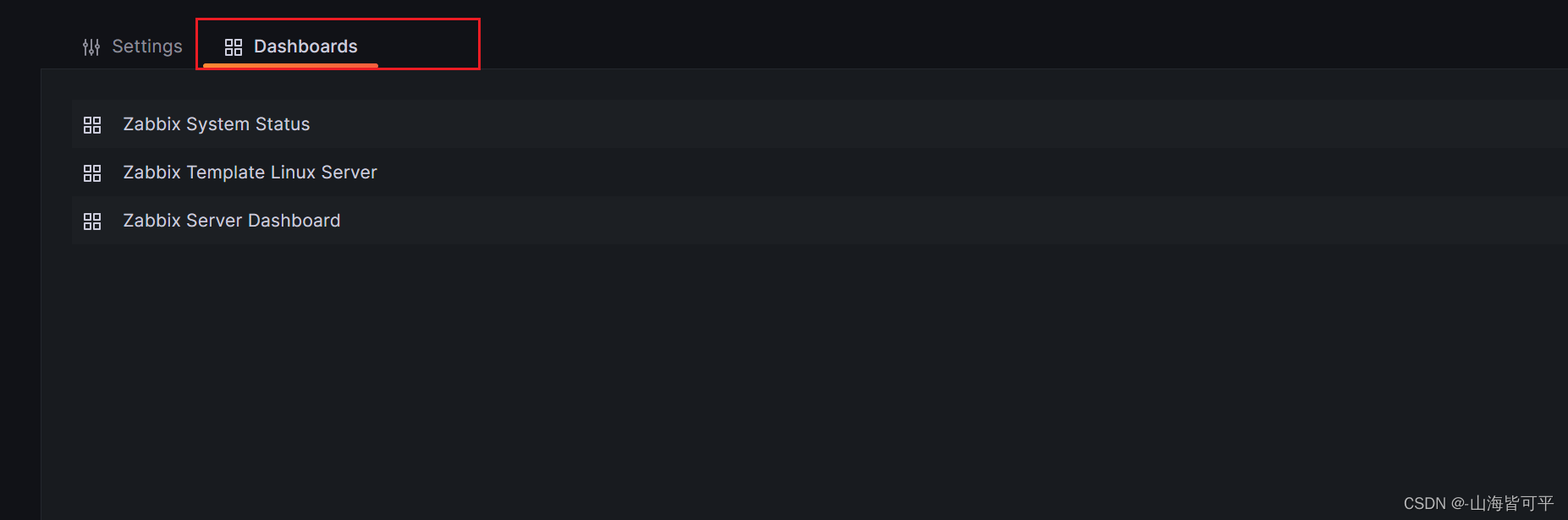
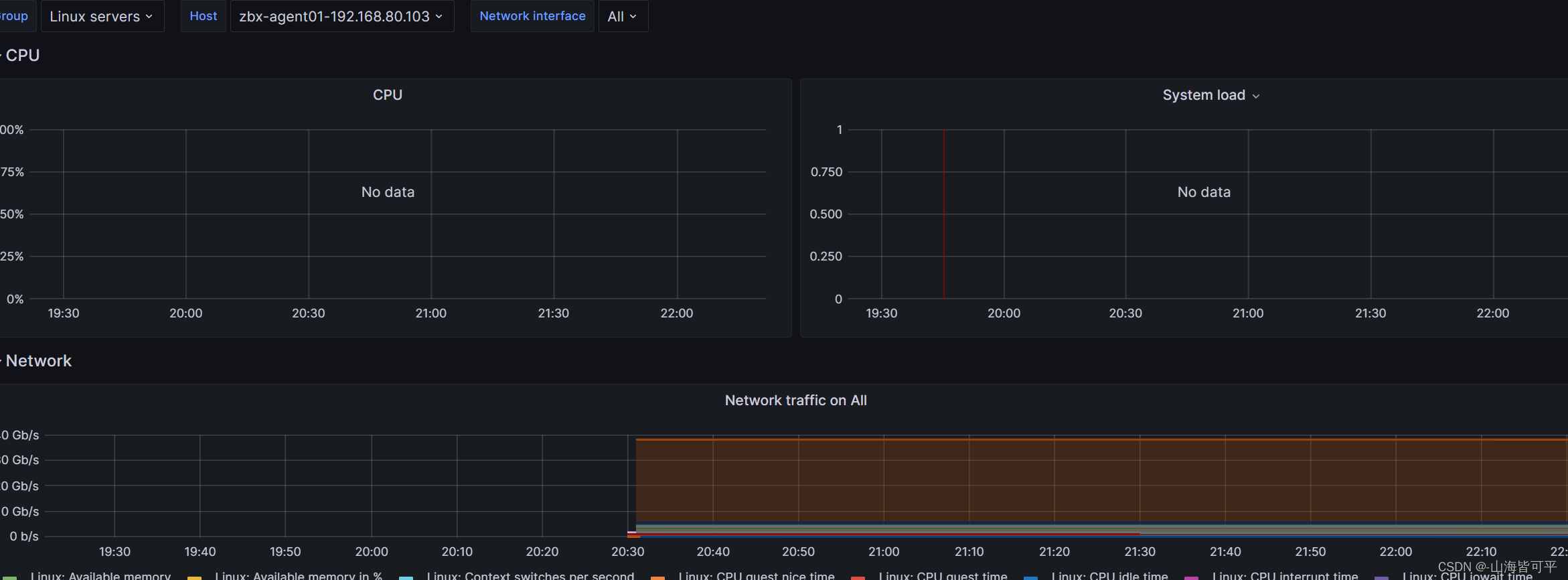
调试模版
调试cpu
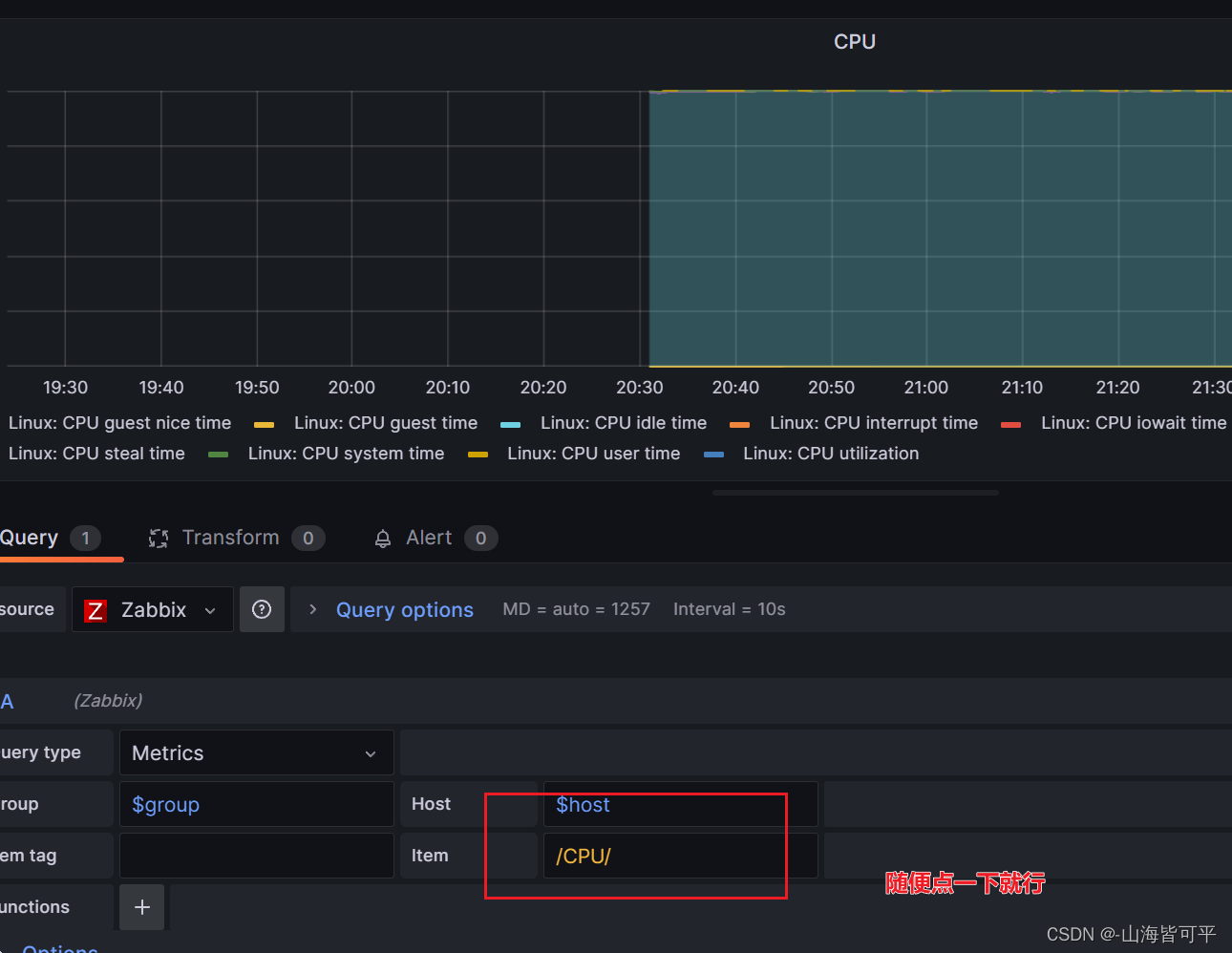

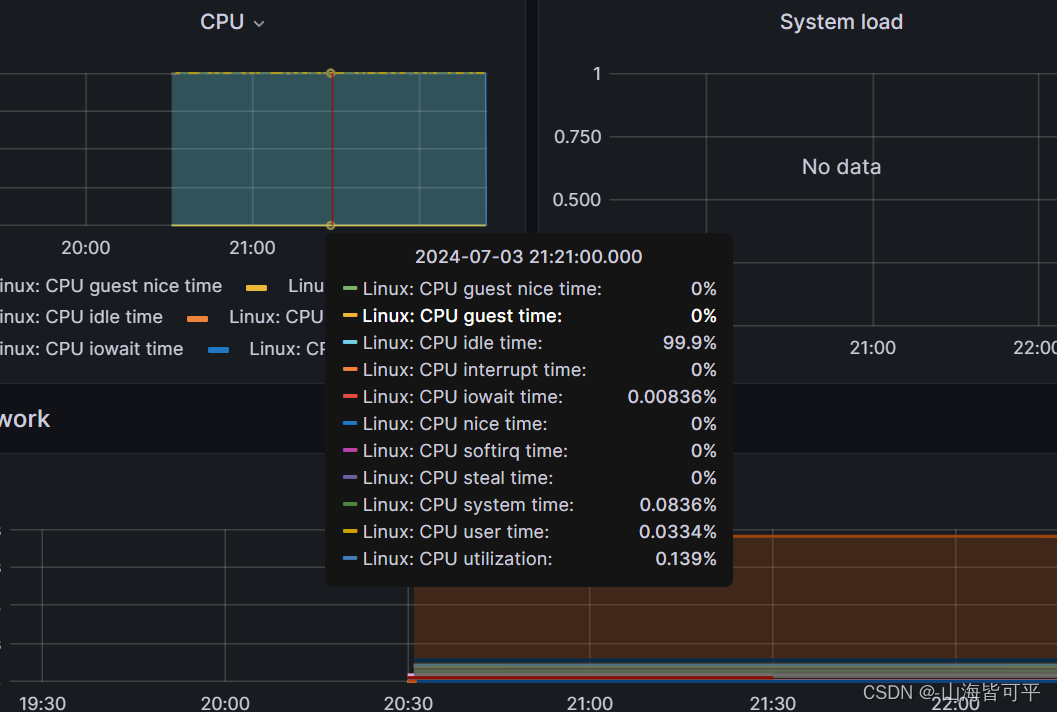
调试平均负载
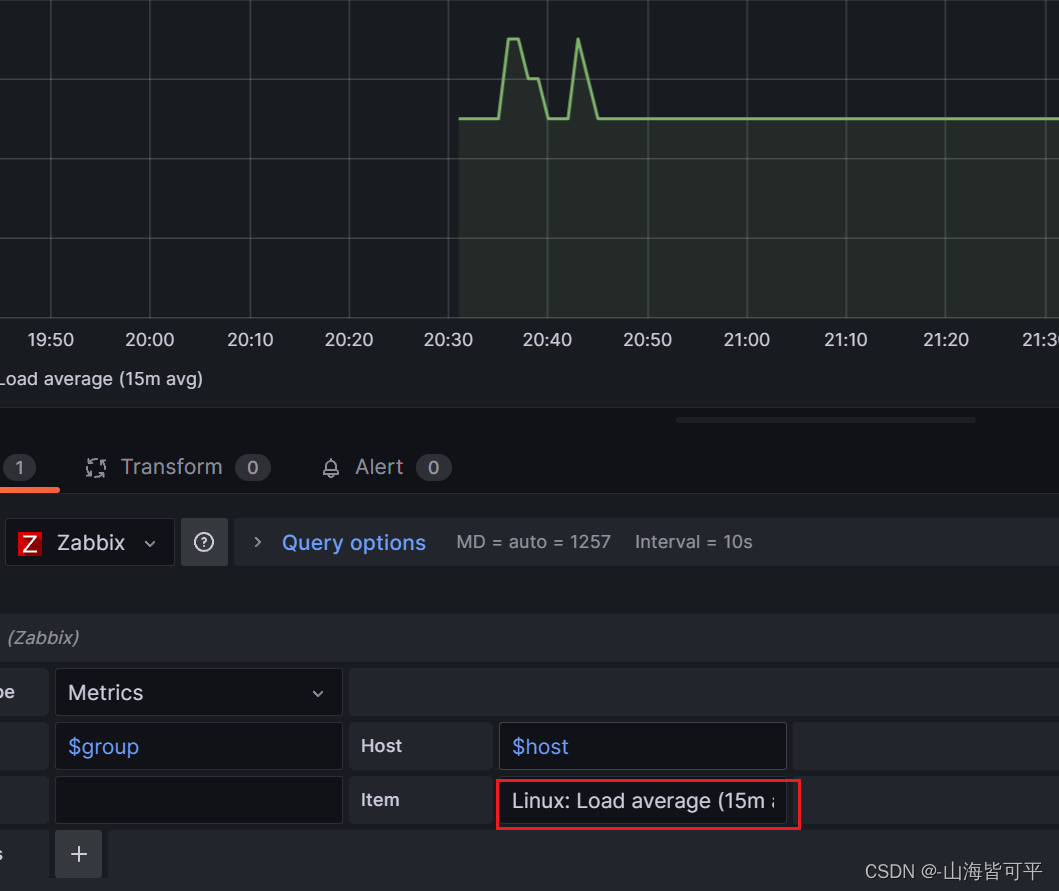

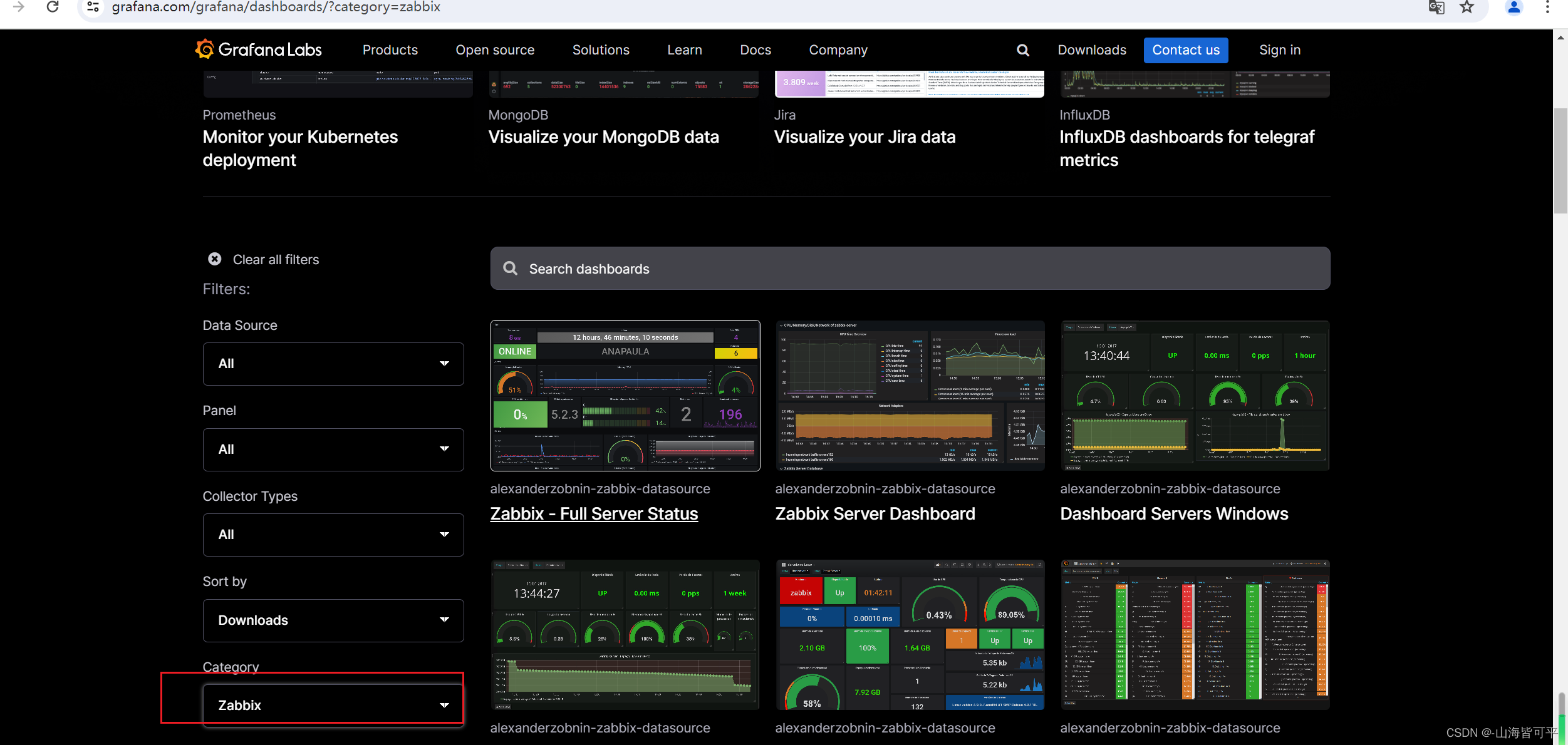
四.如何导入模版
ttps://grafana.com/dashboards 可登录该网站进行