1.概念介绍

1.1 样条曲线的来源

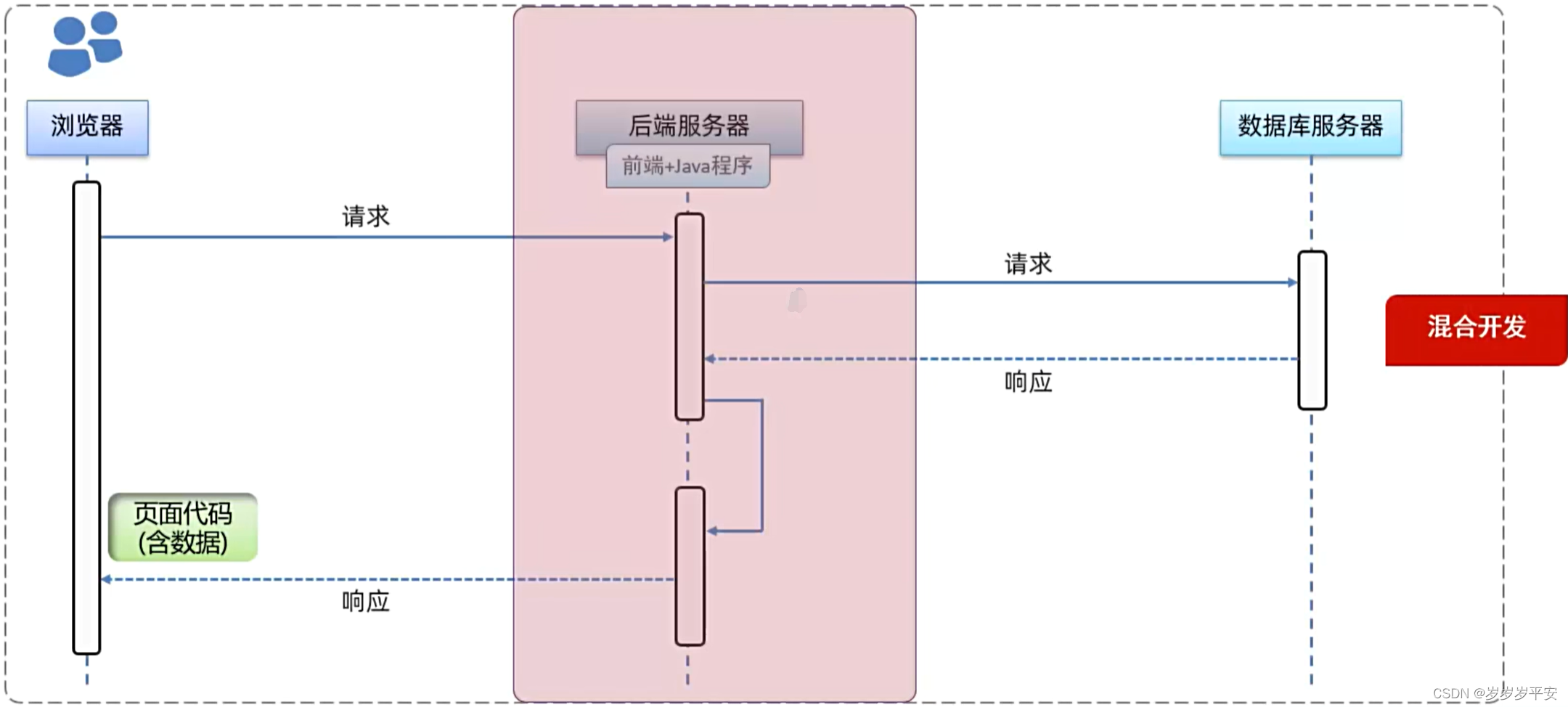
样条的英语单词spline来源于可变形的样条工具，那是一种在造船和工程制图时用来画出光滑形状的工具：富有弹性的均匀细木条/金属条/有机玻璃条，它围绕着按指定位置放置的重物或者压铁做弹性弯曲，以获得所需要的曲线，如下图所示。在计算机科学的计算机辅助设计和计算机图形学中，样条通常是指分段定义的多项式参数曲线。

1.2 非均匀的含义

节点矢量分布不是均匀/准均匀的

1.3 节点重复度

样条曲线按节点矢量中节点的分布情况不同。可以划分为四种类型(假设曲线的次数为k，即：degree = k)。注意所有的节点矢量都应该满足：节点序列非递减。

1.4 有理的含义

指的是NURBS曲线是用有理多项式形式表达式来定义。有理函数是通过多项式的加减乘除得到的函数。在数学中，理性函数是可以由有理分数定义的任何函数，即代数分数，使得分子和分母都是多项式。

2.样条函数分类

2.1 均匀B样条曲线

节点矢量中节点沿参数方向均匀等距分布且重复度均为1，所有节点区间长度

  2.2 准均匀B样条曲线

其节点矢量中端节点具有重复度k+1，所有内节点均匀分布且重复度均为1。

就定义了一个二次(k=2)准均匀B样条基函数。

    2.3 分段Bézier曲线

   2.4 非均匀B样条曲线

对于端节点重复度为k+1的曲线，必定插值于控制多边形的首尾控制顶点。GGP中的NURBS曲线都是该类型的曲线。

2.5 Bézier曲线

一条n次的Bézier曲线可以表示为：

将Bézier曲线方程展开：

当参数u从0变化到1，则得到如下所示的曲线。并且可以看出，Bézier曲线上的一点和所有控制顶点都有关系，移动任何一个控制顶点都会使曲线发生变化。这一点和之后讲的B样条曲线和NURBS曲线不同，这两者具有局部修改性，即：修改任意一个控制顶点，只会影响与该控制顶点相关部分的曲线形状。

2.6 有理Bézier曲线

为什么要用有理曲线：

尽管多项式曲线具有很多优点，但是又很多重要的曲线：如圆/椭圆/双曲线(二次曲线)无法精确地用多项式表示。所有二次曲线均可以用有理函数(即两个多项式相除)表示。为了统一表达，需要引入有理表示。

n次有理Bézier曲线的定义为：

2.7 B样条曲线

为什么要使用分段多项式参数曲线

B样条基函数定义：

是有理基函数。它和B样条基函数有相似的性质(参考B样条基函数的性质)。同样，NURBS曲线和B样条曲线有相似的性质(参考B样条曲线的性质)。

B样条基函数有多种定义方式，这里给出德布尔(de Boor)和考克斯(Cox)的递推定义公式。B样条基函数是定义在被称为节点矢量的非递减参数序列上的函数。

B样条曲线：

p次B样条曲线的定义为：

2.8 非均匀有理B样条曲线(NURBS)

一条p次NURBS曲线定义为：

NURBS曲线/B样条曲线/Bézier曲线的关系：

如果NURBS曲线中所有权因子均为1，那么这条NURBS退化为B样条曲线。如果B样条曲线只有一段，并且节点矢量(只有一段，只存在两个不同的节点值)均为p+1重。那么这条B样条曲线就是Bézier曲线。

3.样条曲面

3.1 张量积曲面

曲线C(u)是单参数的矢量函数(一元函数)，它是直线段到三维空间的映射。曲面是关于两个参数u和v的矢量函数(二元函数)。它表示由uv平面上的二维区域R到三维空间的映射。因此曲面可以表示为S(u,v) = ((x(u,v), y(u,v), z(u,v)),uv属于R。有多种表示曲面的形式，在几何造型中应用最广泛的是张量积曲面。

张量积的方法基本上是在两个方向上均采用曲线的处理方式，它也采用基函数和对应几何系数(控制顶点)的乘积的累加和的形式表示曲面。曲面的基函数是u，v的二元函数，它是由关于u的一元基函数和关于v的一元基函数的乘积来构造。几何系数(在拓扑上)被安排为两个方向的n*m的网格。因此张量积曲面具有如下形式：

3.2 B样条曲面

B样条曲面由两个方向上的控制网格、两个节点矢量和两个单变量的B样条基函数的乘积来定义：

3.3 NURBS曲面

一张在u方向为p次，在v方向为q次的NURBS曲面可以表示为：