RoPE 旋转位置编码，详细解释（下）NLP 面试的女生彻底说明白了

原创 看图学 看图学 2024年07月01日 07:55 北京

书接上文，上文见：这么解释 RoPE 旋转位置编码，女朋友睁大了双眼（上）

下面简单回顾一下上文的重点，后面复数域的解释会用到一些结论，详细的可以点击上面的文章观看。

实数域的 RoPE 解释（重点回顾）

RoPE 的实现和解释，完全可以只在实数域中进行。比如 llama 的实现，就完全没有用到复数的概念。

而在实数域上关于 RoPE 的解释，核心就一句话：在内积空间中，内积具有旋转不变性 。

也就是下面这个性质：

也就是说 两个旋转向量的内积等于其中一个向量旋转它们角度差的结果与另一个原始向量的内积。也可以看作是一个向量逆时针旋转了 , 另一个向量逆时针旋转了 ，然后这两个向量又同时顺时针旋转了 , 于是第一个向量处在 的位置，第二个向量则转到了实数轴上，角度为0. 因为内积的旋转不变性，两个内积依然相等。记住这句话，后面在复数域证明还能用。

复数域的 RoPE 解释

其实涉及到旋转的计算，到复数域里会变得特别方便，因为虚数  i 的物理含义就是旋转。

为了理解虚数/复数，我们先拿负数来做个对比。

负数的出现让人们困惑了很久，我现在有1个苹果，被女朋友拿走了2个，实在是有些脑壳疼。但是现在我们很容易能理解负数，就是欠我一个苹果呗。如果较真的话，那 -1 个苹果在哪里？可能是我从室友那里借了一个。

可以想象一下，在一维的实数轴上，取负可以让1变成-1，再取负又变成1，然后循环。

还有其他的方法能从1到-1么？这时候认知就要提高了，就好像古代人的活动范围很小，那自然认为地球是平的。知道后来可以航海，发现为什么船接近的时候为什么总是先看到船帆然后才看到船的身子，这个时候就开始思考了，地球有没有可能是圆的。

从1到-1如果只在实数轴上移动，那只能是取负。如果把数轴扩展到2维，新增一个虚数轴，那就可以旋转了。1 乘以 i 就跑到虚数轴的上面，再乘以 i 就跑到-1 了。再乘以i就跑到虚数轴的下面，再乘以i就回到了1. 如下图所示：

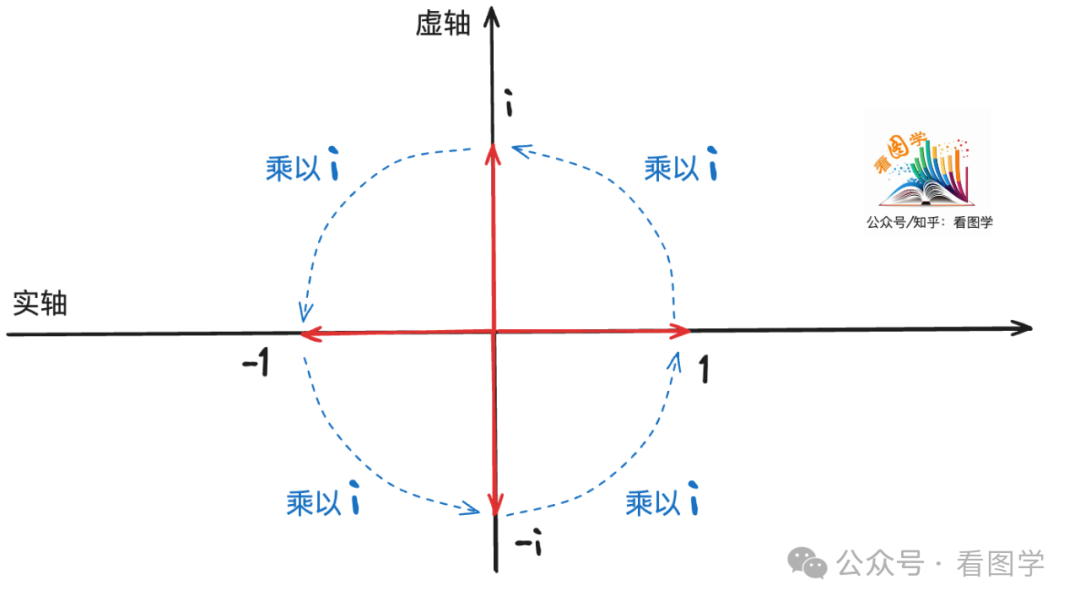
所以为什么 , 其含义就是在复平面上转了2次，从 1 转到了 -1.

欧拉公式  提出来很久之后，大家才尝试从几何的角度去理解欧拉公式。

欧拉公式其实就是在复平面上旋转，复平面是一个2d 平面。为了看的更清楚一点呢，我们再升一维。新增一个与复平面正交的轴代表 x。如下面视频所示。

看图学

，赞16

这个3维空间上就很好的展示了随着 x 的增大， 就一直在旋转的画圈。这个旋转的曲线投影到复平面上，那就是在复平面画圆；如果投影到 x 与 实数轴的平面上，就是 cos 函数；如果投影到 x 与 虚数轴的平面上，那就是 sin 函数。

再回想一下 RoPE 的旋转角度的函数，恰好就是一个 sin 函数和一个 cos 函数，所以说 RoPE 就如同上面欧拉公式的视频一样，在一直转圈，所以叫旋转编码。

然后在实数域证明中，我们已经证明了通过旋转矩阵来解释 RoPE。在复数域一个向量旋转怎么表示呢？非常简单，逆时针旋转  度等于 乘以 . 证明如下：

你看，旋转矩阵又出来了。

所以论文中的

就是 q 和 k 分别旋转了  和 。

复数域中同样满足内积旋转不变性。只不过复数域中的内积不再是简单的相乘，而是要取共轭。

比如复数  和 ，内积定义为：

其中  是  的共轭复数（论文中的共轭是用  来表示的）。

计算复内积：

之所以采用共轭复数，完全是为了满足内积的三个性质：正定性，共轭对称性，第一变元线性。

而共轭复数的物理意义就是顺时针旋转。还记得 逆时针旋转  度等于 乘以 ，那么乘以共轭复数  就是 顺时针旋转  度( 逆时针旋转 - 度)。

复数域的旋转不变性证明如下：

这基本上就是 RoPE 在数学上的解释。

最后论文中就还剩下一个 Re (实部)没有解释。看上面复数的内积公式就可以看出，复数域内积的实部(Re)等于实数域两个向量的内积。也就是

注意左边二维向量的实数域的表示，右边则是复数域的表示。

然后 RoPE 的论文里公式的表示似乎没那么严谨，在论文表述的过程中相同的符号含义发生了变化。所以有时候看上去有些困惑，看完本文和下图的解释应该就明白了。

 

— END —

推荐阅读：

这么解释 RoPE 旋转位置编码，女朋友睁大了双眼（上）

Transformers 中的 Position Embedding 的作用

看图学大模型：Transformers 的前生今世(上）

内积，点积，数量积是一样的么？