源自：系统工程与电子技术

作者：刘世豪  黄仰超  胡航  司江勃  韩蕙竹  安琪

注：若出现无法显示完全的情况，可 V  搜索“人工智能技术与咨询”查看完整文章

摘 要

为提升无人机群辅助边缘计算系统在负载不均衡场景下的性能, 构建了一种新的无人机群边缘计算系统, 利用无人机之间卸载数据来提高计算资源的利用率, 通过联合优化多架无人机的卸载方案、部署和资源分配, 使得系统的时延和能耗加权和最小。该问题高度非凸, 为此提出一种高效的双层优化算法——启发最优评价算法, 上层使用粒子群算法优化无人机位置, 下层在确定位置的情况下使用块坐标下降算法优化无人机的数据卸载和资源分配。仿真结果表明, 所提方案可有效降低系统成本, 与基准策略相比优势明显。

关键词

边缘计算, 无人机群, 任务卸载, 资源分配, 位置优化

引言

随着移动设备的日益增多, 各种新型的移动应用不断涌现, 如导航、图像和视频处理、增强虚拟现实、人脸识别、实时在线游戏和无人驾驶, 这些应用大多具有计算密集性和时延敏感性等特点, 对传统网络性能提出了巨大的挑战[1-2]。为了解决该问题, 移动边缘计算(mobile edge computing, MEC)通过部署设备在用户附近提供高效的服务来缓解用户设备的计算压力[3-4]。但是该方案在部署边缘计算服务器(edge computing server, ECS)时受地理环境制约。由于无人机的灵活性和机动性, 通过无人机平台搭载ECS为用户提供计算服务, 是降低时延和能耗的一种很有前景的方案[5-11]。

单个无人机由于能耗和负载的约束, 计算性能难以适应日益增长的需求, 制约了无人机的应用场景[12-13], 因此关于无人机群的研究越来越多。目前关于无人机群辅助边缘计算的研究包括: 文献[14]在研究无人机部署时, 通过引入差分进化机制, 最小化平均时延来平衡无人机的负载。文献[15]研究了多无人机中继系统的应用, 其中地面终端至少被一个无人机服务, 目标是最大限度地减少提供无线覆盖的无人机数量。文献[16]研究了无人机的部署优化问题, 在确定区域内用最少的无人机取得最大的覆盖范围, 使无人机覆盖时间最大化。文献[17]在用户需求约束下, 通过进化算法联合优化了多架无人机的部署和任务调度, 以最小化系统的能耗。文献[18]通过联合优化无人机的轨迹和资源分配, 以最小化系统能耗, 而且在轨迹优化时增加了无人机之间的防撞策略。文献[19]针对用户关联性, 提出基于压缩感知优化算法以最小化系统的功耗。文献[20]考虑将多个无人机进行角色划分和用户分组, 以便最大限度地利用通信和计算资源。文献[21]通过联合优化多架无人机的轨迹和计算资源, 最小化无人机与用户能耗加权和以确保用户卸载公平性。然而, 文献[21]并没有考虑时延的影响, 文献[22]仅考虑了在单无人机情况下, 通过联合优化计算资源和任务调度, 最小化无人机能耗和时延加权和, 以增强无人机服务的性能, 但在多无人机条件下并没有得到充足的研究。文献[23]研究了多个无人机辅助用户卸载和轨迹联合优化以最小化用户最大时延。文献[24]讨论了无人机群作为用户需要边缘计算服务条件下, 优化了各个无人机的3D位置以最小化服务时延。

以上的无人机群系统研究大多关注无人机的机动性, 并没有充分利用无人机与无人机之间的通信优势。文献[14]虽然利用了无人机的机动性动态选择其服务的用户来均衡无人机的负载, 但是当无人机的机动性受到制约时(例如, 无人机管控政策制约无人机的飞行范围), 无人机服务的区域相对固定, 区域内用户只能选择区域相关的无人机进行卸载[12-13, 25]。由于单个无人机计算性能有限, 用户数据存在随机性, 当无人机的机动性受限时, 导致无人机负载不均衡、计算资源利用不足等问题。而无人机群可以通过无人机之间传输数据来完成各种任务[26-28], 因此可以从全新的角度来解决无人机负载均衡问题。

对于无人机群空中协作场景的研究尚未成熟, 文献[28]讨论了了无人机群在边缘计算的潜力和挑战, 文献[29]中通过将无人机分类, 以满足不同时延受限的服务。文献[30]在无人机群辅助边缘计算条件下, 通过控制无人机计算器件的开关, 决定计算数据是否卸载到其他无人机计算数据。但是以上文献只考虑数据的二元卸载方案, 并没有考虑协作卸载方案以及计算资源优化问题。

本文讨论了一种新的MEC网络结构, 充分利用了无人机通信资源和无人机之间视距链路的优势。在该系统中, 无人机之间可以卸载数据为用户提供服务。为取得系统时延和能耗的加权和最小, 联合优化了多架无人机的部署、任务调度和资源分配。本文工作的主要贡献如下:

(1) 针对无人机群辅助边缘计算系统存在的负载均衡问题, 构建一种新的网络结构, 在该网络中无人机充当ECS和中继, 无人机通过数据的相互卸载缓解负载均衡问题。同时考虑系统的能耗和时延, 构建能耗和时延加权和最小的优化问题。

(2) 为解决上述非凸问题, 提出了双层优化方法——启发最优评价算法(heuristic optimal evaluation algorithm, HOEA)。上层使用粒子群优化(particle swarm optimization, PSO) 算法优化无人机的位置, 下层在给定的位置下优化无人机的数据卸载和资源分配。在实际操作中, 将下层问题分解成两个子问题并使用块坐标下降(block coordinate descent, BCD)算法进行求解。

(3) 与其他方案相比, 所提策略在无人机计算资源不均衡或者数据不均衡的情况下能取得更低的系统成本，尤其是负载不均衡程度加剧时, 效果更为明显。说明可以通过无人机群边缘计算提高无人机的计算资源利用率, 减少系统成本。

1 系统模型与问题描述

无人机群辅助边缘计算模型如图 1所示。

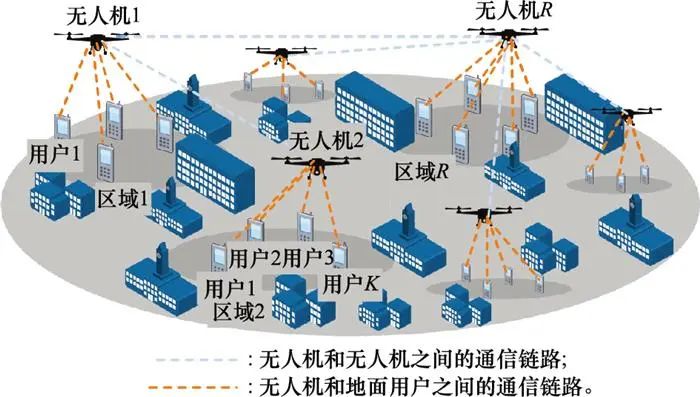
图1   系统模型

图 1中每个阴影部分代表一个区域, 并且每个区域都配备有一个无人机, 称为本地无人机, 每架无人机可以为本区域内的用户提供计算服务, 受无人机管控政策约束, 本地无人机只能在对应区域的上空飞行, 禁止跨区域飞行, 无人机在空中可以进行通信, 并且配备多根天线。系统不考虑用户间的通信干扰。具体而言, 部署R个无人机对应R个区域, 每个区域地面用户有L个, 其中区域的划分r∈R={1, 2, …, R}, R表示区域集合。无人机使用对应的区域进行编号, 区域的范围集合为O={O1, O2，…, OR}, Or表示无人机r能机动的范围, 各区域的用户集合为Lr={1, 2, …, L}, Lr表示区域r内的用户集合。假设每个无人机都装备有MEC服务器, 并且具有通信中继功能。

矩阵A表示无人机之间的连接方案, 矩阵元素ars表示无人机r到无人机s之间的连接状态, ars=1表示无人机r卸载数据到无人机s, ars=0表示无人机r未卸载数据到无人机s, 并且asr和ars含义并不相同。

(1)

1.1 通信模型

假设无人机的高度一定, 为H(单位: m), 区域r的无人机的位置为Qr=(xr, yr), r区域内用户i的位置为

, 假设无人机使用正交频分复用(orthogonal frequency division multiplexing, OFDM)方式与地面用户进行通信。用户到无人机, 无人机与无人机之间通信链路假定为视距链路(link of sight, LOS), 信道的噪声为高斯白噪声。用户到无人机之间的信道功率增益为

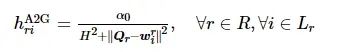
(2)

式中: α0表示发送功率为1 W、距离为1 m处的信道增益; ||·||为欧式范数。那么, 地面区域r中第i个用户到本地无人机的传输速率为

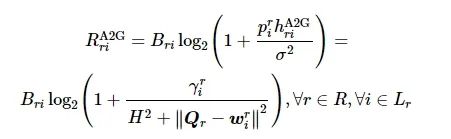
(3)

式中:

表示地面区域r中第i个用户到本地无人机的信道增益; Bri为区域r内第i个用户到本地无人机的信道带宽(Hz); 

表示区域r内地面用户i的发射功率; σ2为噪声功率。

同理, 无人机r与无人机s之间的通信速率为

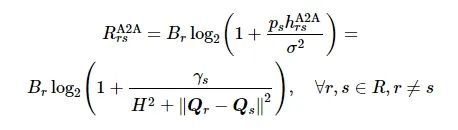
(4)

式中:

表示无人机r和无人机s之间的信道增益; Br为区域r内本地无人机与其他无人机通信的信道带宽(Hz); γs=psα0/σ2, ps为区域r本地无人机与其他无人机通信的功率, σ2为高斯白噪声的噪声功率。

1.2 时延模型

假设地面用户k的任务记为{ck, ik}, ik为用户k计算数据大小(bit), ck表示用户k计算任务执行1位数据时所需ECS的中央处理器(central processing unit, CPU)周期数(cycles/bit)。用户在向本地无人机进行卸载时, 采用全卸载方案, 无人机向无人机卸载数据时, 采取协作式卸载方案。

时延主要有3个方面, 地面用户到无人机的传输时延, 无人机本地计算需要的时间, 以及无人机卸载到其他无人机传输数据的时延和数据计算的时延, 其中无人机计算数据和卸载数据可以同时进行。在本文中忽略结果回传所需的时延和能耗。区域r内i用户卸载数据到本地无人机的时延为

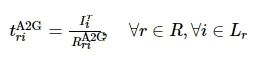
(5)

式中: 

表示在区域r内i用户的数据量; 

为区域r内i用户到本地无人机的通信速率。

本地无人机计算时延为

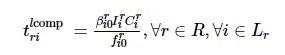
(6)

式中: 

为区域r内i用户本地卸载因子; 

为本地无人机计算的数据; 

为区域r内i用户计算1 bit所需的ECS的CPU周期数;

是本地无人机为区域r内i用户分配的计算资源。

第s个无人机卸载i用户数据到第r个无人机的传输时延为

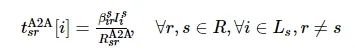
(7)

式中: 

表示区域s内i用户的数据; 

表示区域s内i用户卸载到无人机r的比例。

为简化问题, 无人机向目标区域分配的计算资源被目标区域内用户平均占用。第r个无人机计算s区域i用户卸载数据的时延为

(8)

式中: 

表示无人机r分配给区域s内i用户的计算资源; 

表示无人机r分配给区域s的计算资源。

在本文中无人机计算数据和卸载数据可以同时进行, 所以区域r内i用户计算的时延为

, 其中

为区域r内i用户的数据从无人机r卸载到无人机s所需传输和计算的总时延, 由于无人机可以同时向多个无人机卸载数据, 则区域r内i用户的数据在无人机群中传输和计算的时延为

, 则整个系统的用户时延为

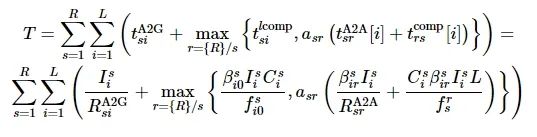
(9)

1.3 功率模型

无人机r与其他无人机通信所消耗的能量为

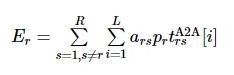
(10)

无人机的计算功耗包含两部分, 计算本地数据能耗以及计算其他无人机卸载的数据能耗。本文中使用文献[31]中的能量计算模型, 无人机r的计算能耗为

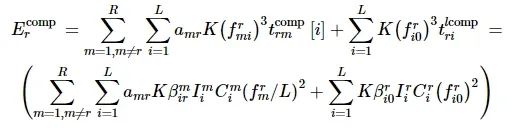
(11)

式中: K为CPU架构的有效开关电容。

系统中用户传输数据的总能量为

(12)

无人机计算能耗和通信能耗的总和为

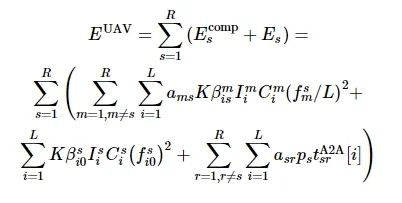
(13)

1.4 问题描述

假设地面用户位置和计算任务量已知, 无人机的部署、资源分配、数据卸载比例和连接方案分别为Q, f, β, A。为提升无人机群边缘计算系统在负载不均衡场景下的效果, 通过联合优化用户卸载比例、无人机的部署和计算资源分配最小化系统成本。优化问题表示为

(14)

式中: χ={Q, A, β, f}是变量; fmaxs为第s个无人机最大的计算频率; 目标函数ρT+EUAV+EUE称为系统成本; ρ为能量与时延相对权重[22, 32]。约束C1, C5和C6保证卸载数据非负以及数据全部被计算, 约束C2, C7和C8保证计算资源非负以及计算资源全部被使用, C3使用二进制数据表示无人机之间的连接状态, C4保证无人机在对应的区域内飞行。

2 优化问题求解

原优化问题为非凸问题, 一般的优化算法不容易解决。启发式算法由于和梯度无关, 有利于解决该问题。由于无人机的位置和任务分配是紧密耦合的, 因此单独使用启发式算法不太合适。受文献[17]启发, 本文采用分层优化算法, 上层使用PSO算法优化无人机的位置, 而下层以最优资源分配方式对该位置进行评价。对于无人机之间的连接方案, 考虑实际情况的限制, 可以很明显地减少备选连接方案。

2.1 连接方式

如果对上层的连接方式直接进行遍历, 若有R个无人机, 则有2R×(R－1)种连接方式, 当无人机数量很多时, 该方式不合理。但是通过观察发现一些无人机连接情况是不可能出现的, 通过消除这些不可能出现的连接能很大程度缩小可行域。在实际场景中, 当无人机提供向其他无人机卸载数据时, 便不再向其他无人机提供计算服务。在本文中无人机的连接方式使用矩阵A中元素ars表示, 当无人机ars=1, 表示无人机r向无人机s卸载数据, 则此时所有的无人机都不会向无人机r卸载数据, 则无人机之间卸载约束为

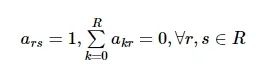
(15)

使用无人机卸载的目的是为了均衡负载, 通过定义辅助变量

初步衡量计算资源占用情况, 其中Ir为区域r内用户的数据总量, 目的是减少无人机的计算资源占用差距。在本文中, 计算资源占用大的无人机倾向于向计算资源占用小的无人机卸载数据, 协同完成计算任务。当无人机r计算资源占用最大, 则无人机r会选择和其他无人机协同完成计算任务, 但是无人机r并不会接受其他无人机的计算任务, 则分别有:

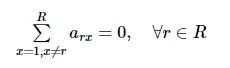
(16)

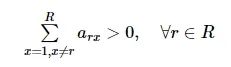
(17)

计算资源占用大的向计算资源占用小的卸载, 反之则不会, 即在Gr>Gs, r, s∈R条件下, 无人机r到无人机s可以选择卸载和不卸载数据两种状态, 但是无人机s却不能卸载数据到无人机r, 可表示为

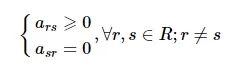
(18)

通过上述分析可以很大程度上缩减寻找最优连接方式的范围, 如算法1所示。

2.2 HOEA

多无人机的位置优化是一个非凸的问题, 并且各个无人机之间位置选择是相互耦合的, 这对优化有非常大的影响, 导致一般的优化方法很难解决, 因此考虑使用启发式算法求解。本文采用标准PSO算法[33], 但是传统的PSO算法很难解决无人机位置与任务调度紧密相关的问题, 为此以PSO算法为基础, 将PSO和凸优化方法结合, 解决无人机位置和任务调度的紧密相关的问题。将原问题分解成两层问题, 上层算法使用PSO算法寻找多个无人机的部署, 下层算法在给定无人机部署情况下, 以最优任务调度评估多无人机的部署, 用以粒子的更新。

给定无人机部署Q和连接方式A条件下, 下层的问题可以表述为

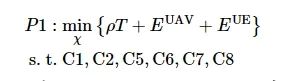
(19)

定义一个辅助变量

。则P2问题变为

(20)

式中: C9和C10保证了将服务延迟线性化后和原问题等价, 但是线性化之后, 问题依然非凸, 则在本文中采用BCD算法将其分成两个子问题。

子问题1:计算资源分配优化

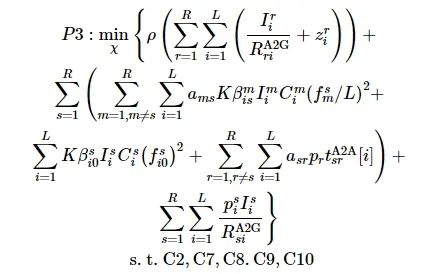
(21)

式中: 变量χ={f}; C2, C7, C8表示每个无人机计算资源受限并且分配的资源非负。由于目标函数为凸的, 约束为凸, 则该问题为凸优化问题, 使用CVX工具箱进行求解。

子问题2:数据分配优化

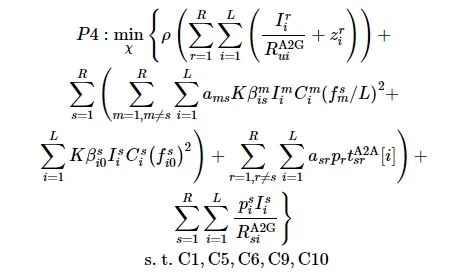
(22)

式中: 变量χ={β}; 约束C1, C5和C6表示全部数据被计算以及数据分配非负。该目标函数对变量β是仿射的, 并且约束为凸, 所以该问题为凸优化问题, 使用CVX工具箱进行求解。

BCD资源分配算法展示如算法2所示。

算法3中采用了PSO算法框架, 其中

为无人机位置在粒子群算法的表示。

表示在Pjs(第s次迭代第j个粒子位置)的效用函数, 通过算法2进行计算。基于PSO算法的特点, 利用粒子的速度和局部最优值以及之前迭代的全局最优值来计算当前粒子的速度, 则可以表示为

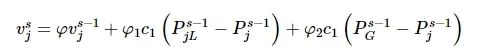
(23)

式中: 

为局部最优值；

为第s－1次迭代的全局最优值；φ1和φ2是学习系数；c1和c2是正的随机数；φ为惯性系数。粒子当前的速度决定下一次迭代的粒子位置, 则粒子位置表示为

(24)

对粒子的边界进行处理, 使用算法2计算效用函数, 更新每个粒子的全局最优值和局部最优值, 直至达到最大迭代次数Smax。

本文提出了无人机部署、卸载方案和计算资源联合优化解决方案, 在给定无人机连接情况下, 通过PSO算法进行无人机位置部署, 使用BCD算法进行任务卸载和计算资源分配。HOEA算法的伪代码展示如算法3, 图 2展示了该算法的流程图。类似文献[34]分析, 整个算法的复杂度主要受PSO算法和BCD算法影响。PSO算法的复杂度取决于粒子维度大小Np和最大迭代次数Smax, 在最坏的情况下复杂度为O(NpSmax)。计算资源分配和任务调度优化算法使用BCD算法, 该算法最大复杂度约为O((N+M)Gmax), 其中Gmax为迭代的最大次数, N和M分别为计算资源优化的变量数和任务分配的变量数，则整个算法的复杂度为O(NmaxNp(N+M)GmaxSmax)。

算法3   HOEA算法描述    

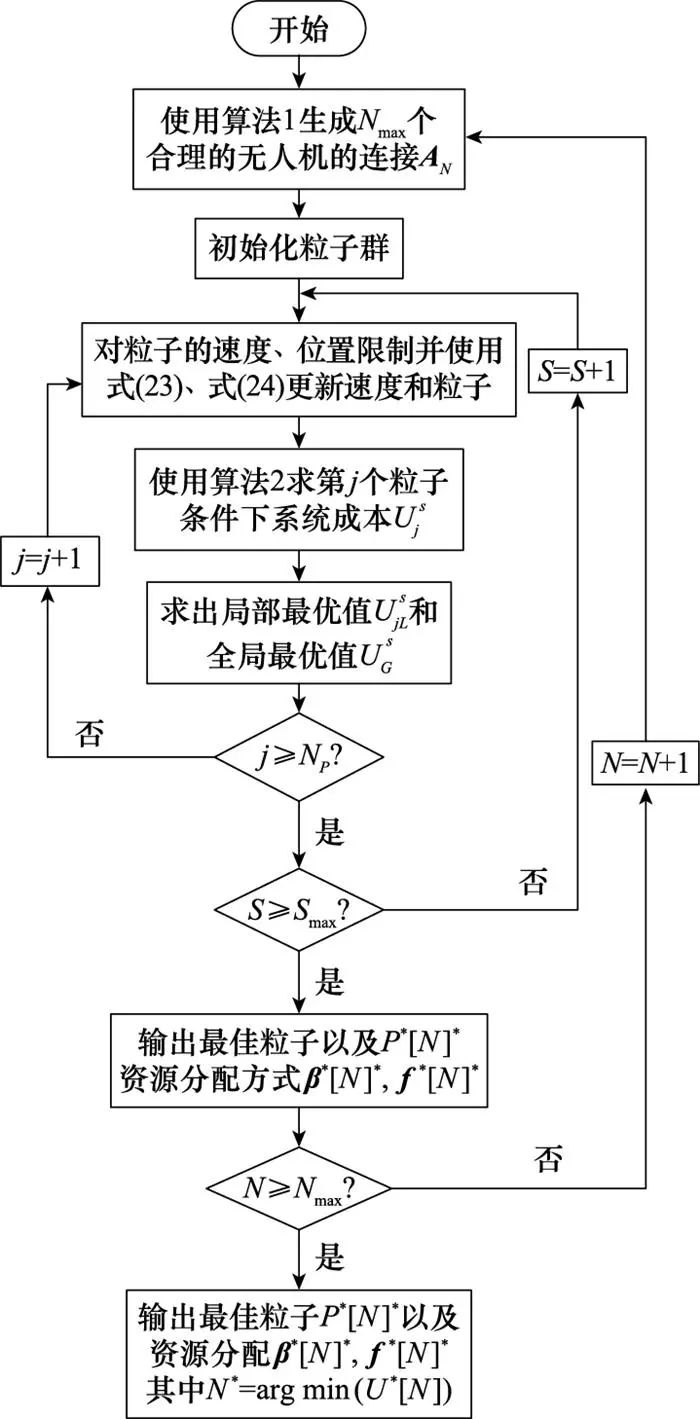
图2   算法3的流程图

3 仿真结果分析

本节中仿真环境为配置英特尔i7-12700H, 2.3 GHz和32 G RAM的计算机, 以验证系统的可行性和所提策略的有效性。该场景下区域数量R=4, 无人机数量R=4, 每个区域内的地面用户数量L=5, 水平位置分布在边长为4 000 m的正方形区域, 该区域被平均分成4个区域。区域分布和编号如图 3所示, 用户随机分布在区域内。表 1为仿真参数。

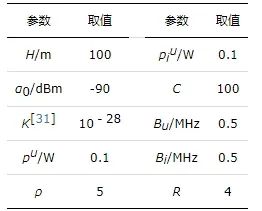
表1   仿真参数

3.1 位置优化的优势

假定各无人机的计算性能为

, 区域内的每个用户数据相同, 不同区域用户数据分别为

, 其余参数设置如算法3所示。为探究无人机部署优化的有效性, 制定以下两种方案: ①无人机部署和任务调度联合优化方案; ②无人机随机部署条件下的任务调度方案, 即无人机在随机的部署下以最优资源调度为地面用户提供计算服务。

图 3展示了无人机的移动方向和无人机连接情况。无人机1会把本地的数据向其他的3个无人机进行卸载, 使用矩阵A表述为[0111;0000;0000;0000]。图 4展示了所提算法与PSO算法在矩阵A=[0111;0000;0000;0000]条件下的性能对比, 所提算法和PSO有类似的收敛速度。但是所提算法相比PSO能取得更小的系统成本, 因此所提算法优于PSO算法。

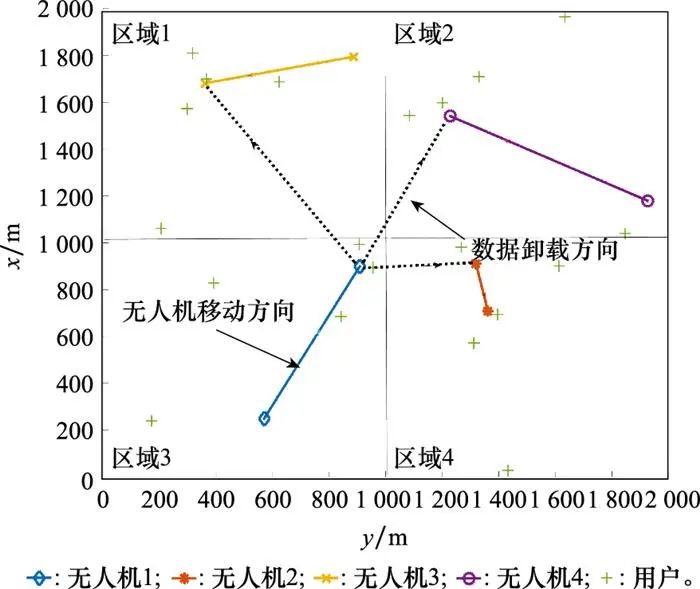
图3   无人机位置变化和连接图

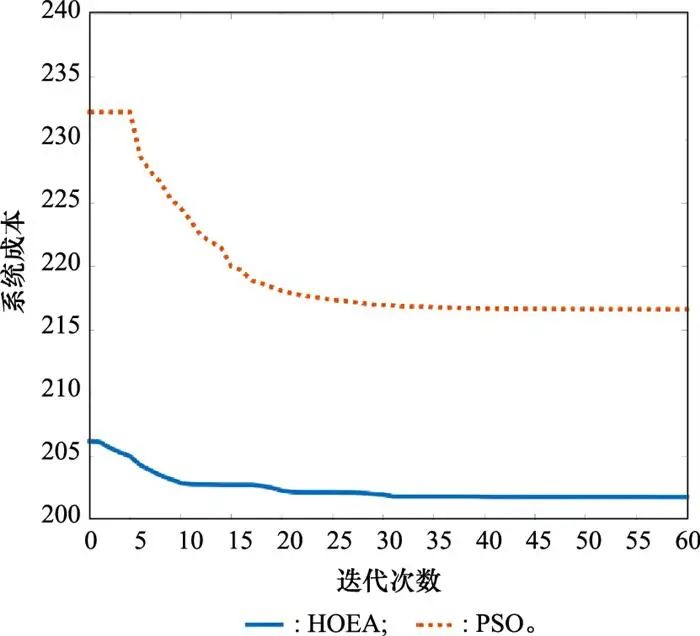
图4   算法收敛性

表 2展示了有无位置优化下的系统成本。无人机位置部署优化受到地面用户和卸载无人机的影响, 具体来说用户将数据卸载到本地无人机时, 无人机的部署会影响用户传输能耗和传输时延, 当无人机向其他无人机卸载数据时, 无人机之间的距离同样会影响无人机传输能耗和传输时延。当无人机随机部署时, 对用户和无人机能耗和传输时延造成影响, 因此无人机部署是有必要的, 表 2仿真数据证明了无人机部署优化的必要性。

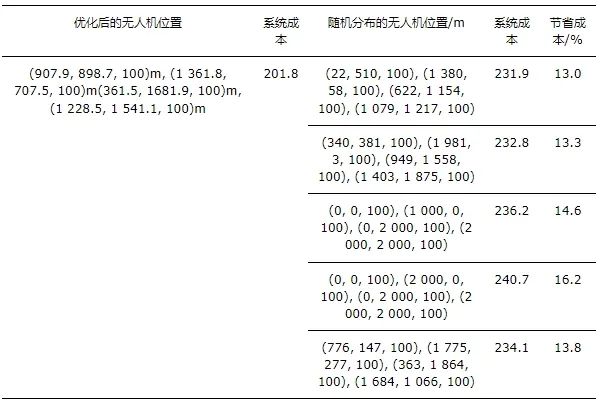
表2   有无位置优化对比

3.2 所提策略优势

为探究所提策略的优势, 将与以下两个方案进行对比。方案1:多个无人机共同服务用户, 用户只能将数据卸载到本地无人机, 无人机之间不相互卸载数据, 且本地无人机都在最优的位置提供计算服务, 且使用HOEA。方案2:无人机之间可以相互卸载数据, 但是每个无人机最多只能向一个无人机卸载数据, 并且在最优的位置卸载数据, 且使用HOEA。

3.2.1 数据变化的影响

为探究数据变化对系统性能的影响, 考虑无人机的计算频率为

, 初始时, 各区域中地面用户的数据分别为

, 通过增大区域1中用户的数据量来模拟系统出现数据分布不均衡问题, 其余的参数设置和表 1相同。

图 5展示了不同策略和算法随着数据量变化的情况, 随着区域1中用户数据量的增大, 所提策略和算法的优势就越明显。图 6展示了区域内一个用户的数据卸载比例变化, 同区域的其他用户卸载情况与之类似。

表示区域1内地面用户卸载到对应无人机2到无人机4的比例。而

对应区域2到区域4内地面用户向本地无人机卸载的比例, “其他”表示区域2到区域4内用户向非本地无人机卸载数据的比例。图 6说明了随着区域1用户数据量的增大, 也即数据不平衡程度增大时, 无人机1卸载到其他无人机的比例增大。当局部数据增大, 会导致单个无人机的负载变大, 因此负载大的无人机便向负载小的无人机卸载数据, 也即无人机连接方案为A=[0111;0000;0000;0000], 并且随着数据量的增大, 向其他无人机卸载的数据也会相应增大。结合图 5和图 6可以看出, 在各个区域数据量相同的情况下, 地面用户只选择本地无人机进行卸载, 此时所提方案、方案1和方案2三者等价。当区域数据量增大时, 卸载的成本小于卸载带来的收益, 负担重的无人机会向多个无人机卸载, 此时所提方案不再和方案1等效, 所提方案展现出优势, 并且随着数据的不均衡程度的加深, 所提方案的优势更加明显。

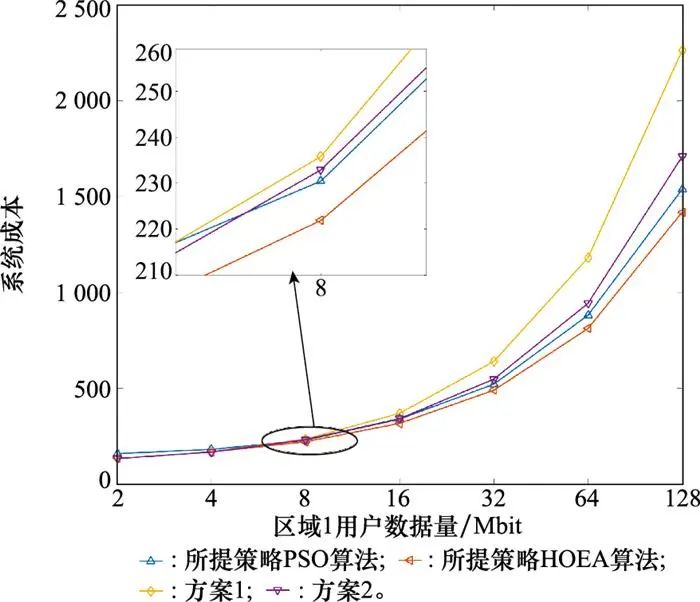
图5   系统成本随区域1数据量的变化

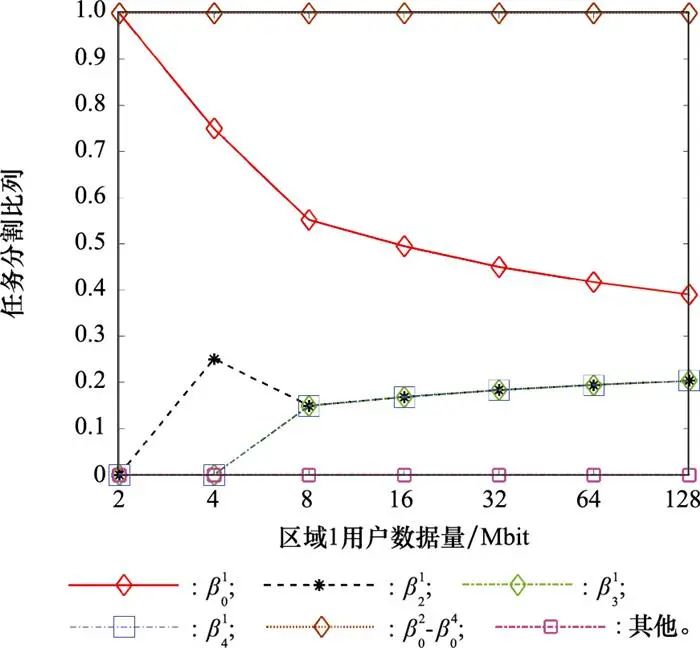
图6   各区域卸载比例随区域1数据量的变化

图 7展示了在所提策略下无人机随区域数据变化的轨迹。无人机部署随着区域数据的变化而变化, 尤其随着数据不平衡程度的加深, 无人机位置变化剧烈, 无人机会相互靠近以此来减少数据传输所带来的时延和能耗。

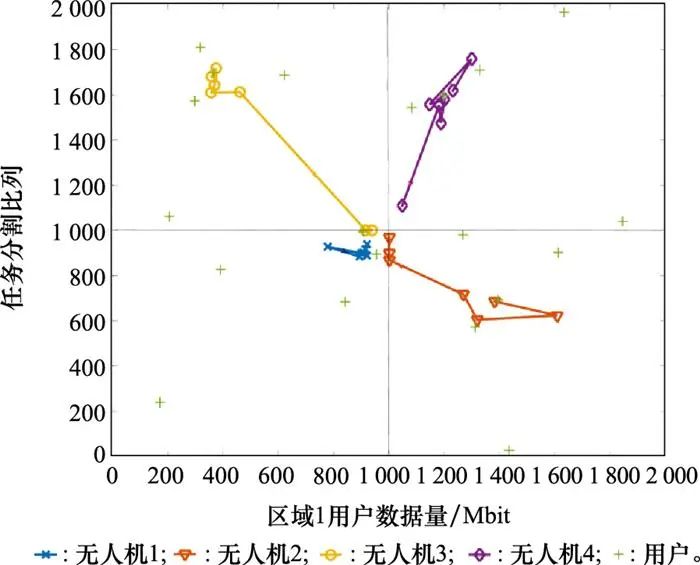
图7   无人机位置随着计算性能的变化

3.2.2 计算性能变化的影响

为探究数据变化对系统性能的影响, 区域中地面用户的数据为

, 初始时无人机计算频率为

, 通过增大无人机1的CPU频率来模拟系统出现计算资

源分布不均衡问题, 其余的参数和表 1相同。

图 8比较了3种策略在不同计算性能下系统成本的大小, 所有策略下系统成本都随着无人机1计算频率的增大而减小。随着无人机1计算性能的增加, 所提策略相比其他策略就越有优势。

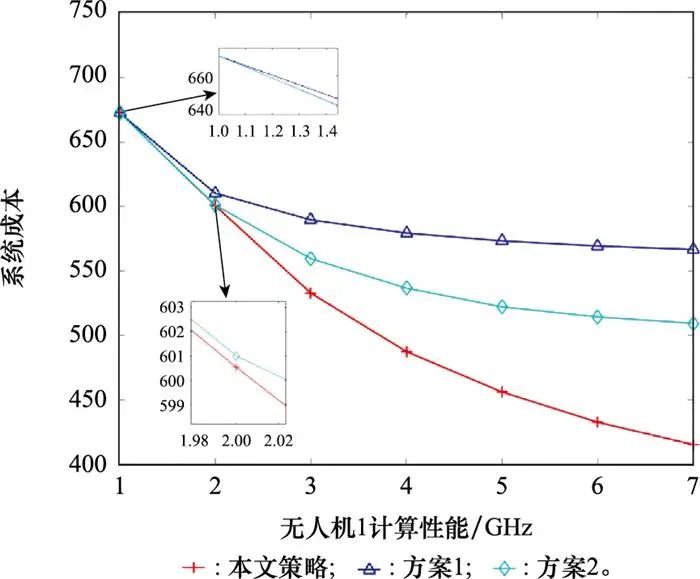
图8   3种策略系统成本随无人机1计算资源的变化

从图 9(b)~图 9(d)中可以看到, 随着无人机1计算性能的增大, 其他无人机卸载到无人机1上的比例也越大。图 9(a)说明, 当无人机1计算性能强于其他无人机时, 区域1内的用户数据全部被本地无人机所计算。当无人机之间计算性能相同时, 无人机全部采用本地计算的方式, 此时所提方案、方案1和方案2三者相同。当无人机之间计算性能差异增大时, 计算性能强的无人机所在的区域会选择全部本地计算, 计算性能弱的无人机会向其他无人机卸载数据。从图 10中可以看到, 无人机计算性能的变化对整个无人机的位置并没有明显的影响。

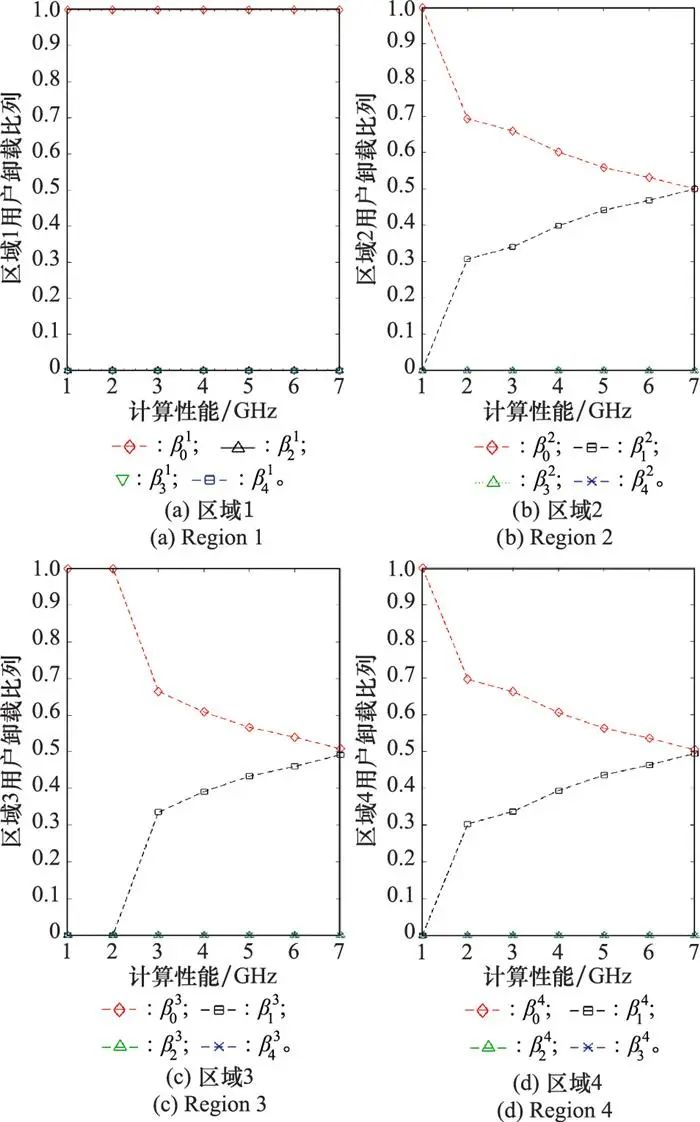
图9   各区域卸载比例随无人机1计算性能的变化

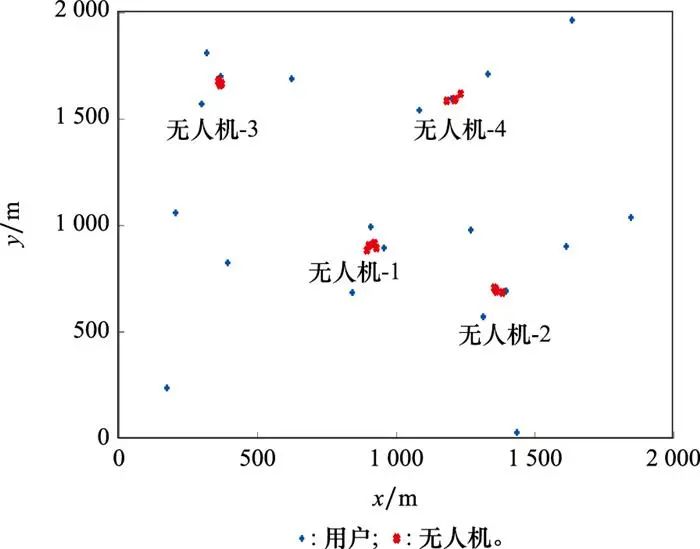
图10   无人机位置随着计算性能的变化

4 结束语

本文构建了无人机群辅助边缘计算的网络模型, 通过设计无人机和无人机之间、无人机和用户之间的信息交互以实现在数据或计算能力不均衡的情况下, 缓解无人机计算负担, 实现整个系统的成本最小化。所提HOEA以PSO为基础, 联合优化了多无人机卸载、部署和资源分配方案, 并通过仿真验证了所提算法的有效性。此外, 文中提出的优化方法可以适用于无人机辅助通信场景下, 无人机位置部署和资源分配问题变量耦合的相关问题。在后续的研究中, 考虑引入动态多无人机场景, 设计无人机的轨迹和任务分配策略, 以取得更好的系统性能。此外, 无人机群辅助边缘计算场景下数据卸载的安全性也需要格外重视。

声明:公众号转载的文章及图片出于非商业性的教育和科研目的供大家参考和探讨，并不意味着支持其观点或证实其内容的真实性。版权归原作者所有，如转载稿涉及版权等问题，请立即联系我们删除。

注：若出现无法显示完全的情况，可 V  搜索“人工智能技术与咨询”查看完整文章