题目
树可以看成是一个连通且 无环 的 无向 图。
给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ,edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。
请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的边。
示例 1:
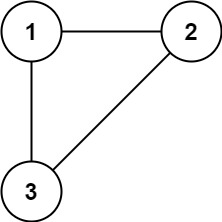
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]
示例 2:
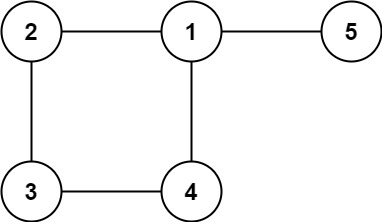
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]
提示:
n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ai < bi <= edges.length
ai != bi
edges 中无重复元素
给定的图是连通的
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/redundant-connection
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解决方法
fun findRedundantConnection(edges: Array<IntArray>): IntArray {
//定义一个表示父节点的数组
val intArray = IntArray(edges.size + 1) { it }
for (i in edges.indices) {
//寻找第一个父节点
var p1 = findParent(edges[i][0], intArray)
//寻找第二个父节点
var p2 = findParent(edges[i][1], intArray)
//如果这两个父节点一致 说明两个节点是在同一个跟节点上 现在这两个节点链接 势必会造成环 所以直接返回这条边即可
if (p1 == p2){
return edges[i]
}else{
//如果这两个父节点不一致 则归并
intArray[p1] = intArray[p2]
}
}
return intArrayOf()
}
fun findParent(num: Int, arrays: IntArray): Int {
//寻找父节点 如果父节点的值为自己 那么就说明找到了
var temp = num
while (arrays[temp] != temp) {
temp = arrays[temp]
}
return temp
}
总结
1.没有专门学过算法的话,这道题还是需要一些思考的,你可能写不出来
2.我也是看了很多的文章才看懂并查集