- 优先图(Precedence Graph)
- 视图可串性
- 多重图(Polygraph)
优先图(Precedence Graph)
优先图用于冲突可串性的判断。
优先图结构:
- 结点 (Node):事务;
- 有向边 (Arc): Ti → Tj ,满足 Ti <s Tj;
存在Ti中的操作A1和Tj中的操作A2,满足A1在A2前,并且A1和A2是冲突操作(对同一个元素进行:读写、写读、写写)。
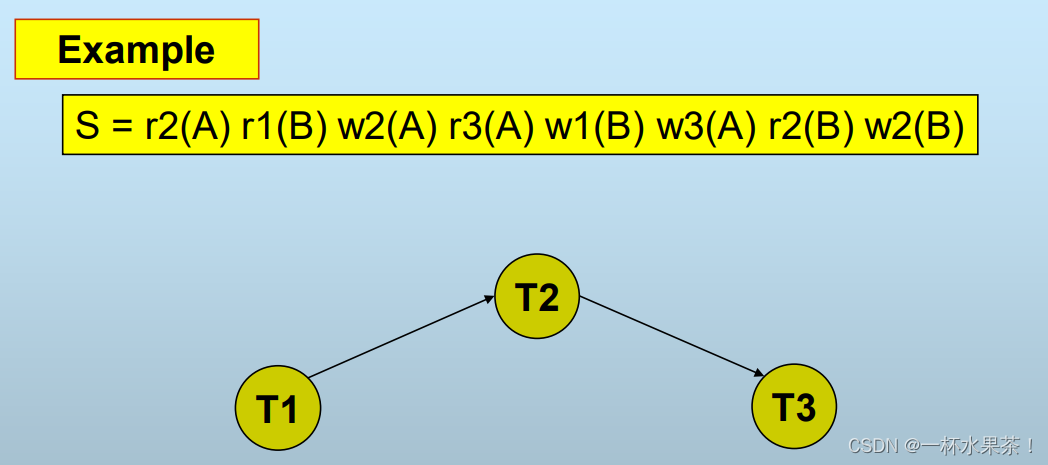
S 中,
- 先考虑元素 A,r2(A) w2(A) r3(A) w3(A),很明显,r2(A) 和 w3(A) 、w2(A) 和 w3(A) 是冲突操作,所以画一条有向边,从 T2 指向 T3。
- 再考虑元素 B,r1(B) w1(B) w2(B),r1(B) 和 w2(B)、w1(B) 和 w2(B) 是冲突操作,所以画一条有向边,从 T1 指向 T2。
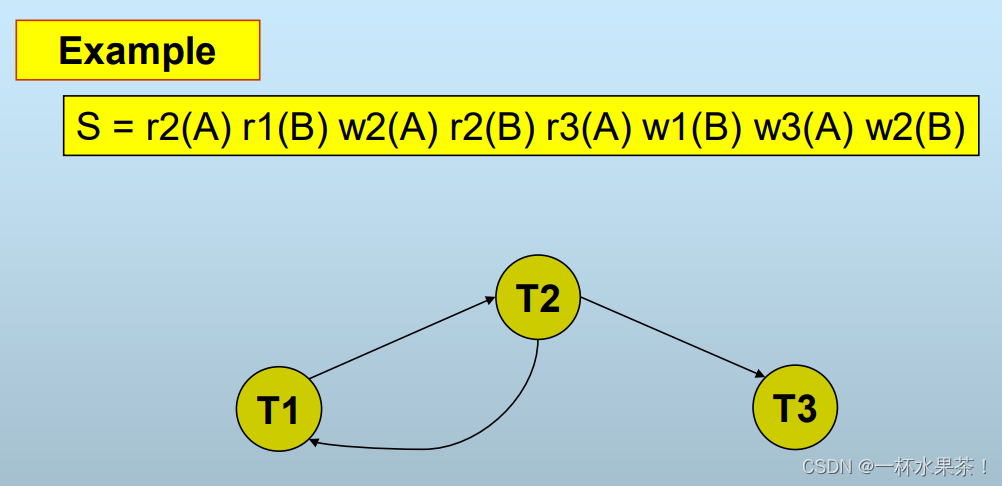
给定一个调度S,构造S的优先图P(S),若P(S)中无环,则S满足冲突可串性。
视图可串性
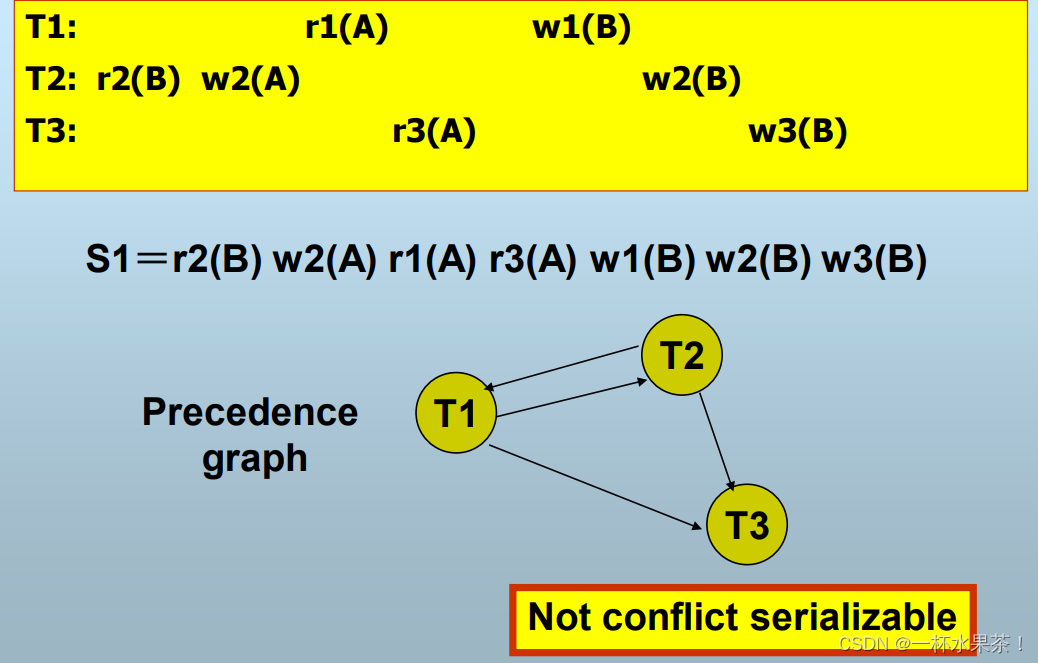
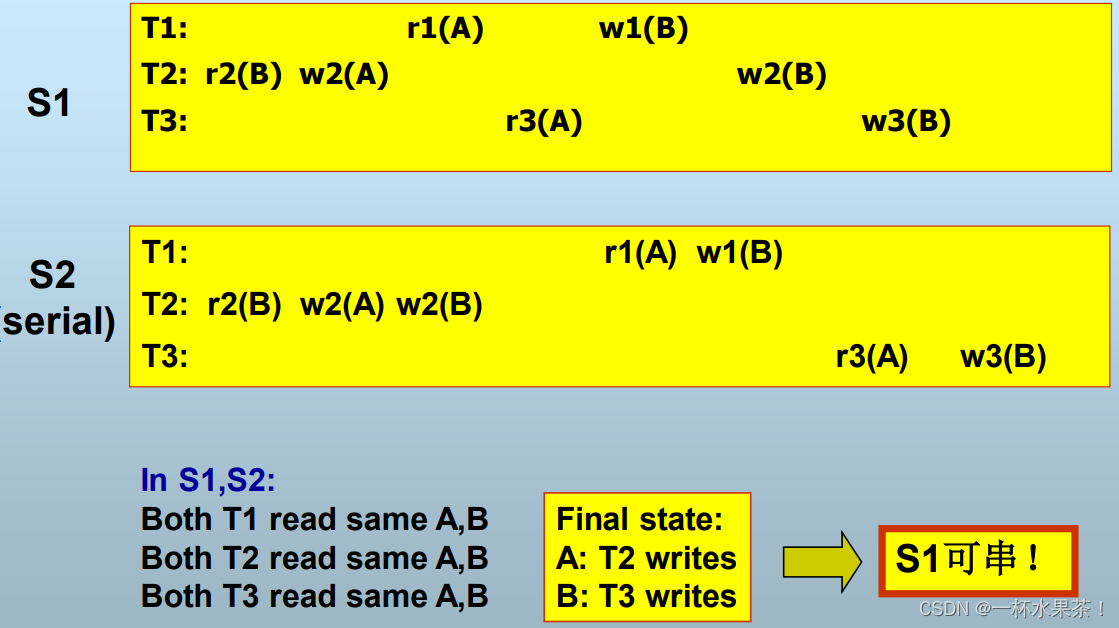
如果按照conflict serializability,S1不可串,实际上S1可串。View serializability 解决了 Conflict serializability 过于严格这一问题。
S1和S2中任何事务的读操作的源都相同。

区别:
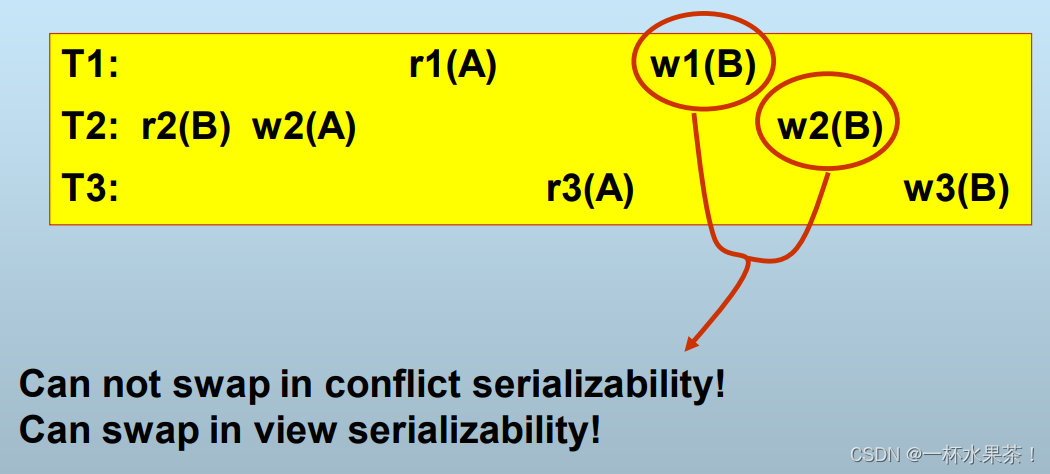
多重图(Polygraph)
视图可串性判断:多重图 (Polygraph)。
对于调度Z,其Polygraph为LP(Z)。
结构:
- Node:事务+假想的事务Tb和Tf
- Arcs:事务(包括Tb和Tf)之间
(1) Tb对所有DB元素执行写操作,构成DB初始状态
(2) Tf读所有DB元素,得到DB终态
(3) 建立Arcs
(3a) If wi(A) ⇒ rj(A) in S, add Ti → Tj
(3b) For each wi(A) ⇒ rj(A) do
consider each wk(A): [Tk ≠Tb]
- If Ti ≠Tb ∧ Tj ≠Tf then insert
Tk → Ti some new p
Tj → Tk
- If Ti =Tb ∧ Tj ≠Tf then insert
Tj → Tk
- If Ti ≠Tb ∧ Tj =Tf then insert
Tk → Ti
(3c) 对于每一对 Ti → Tj, 选择其中一个,将其在Polygraph中删除,
如果能使Polygraph成为无环图,则调度S是视图可串化的 (V-S)
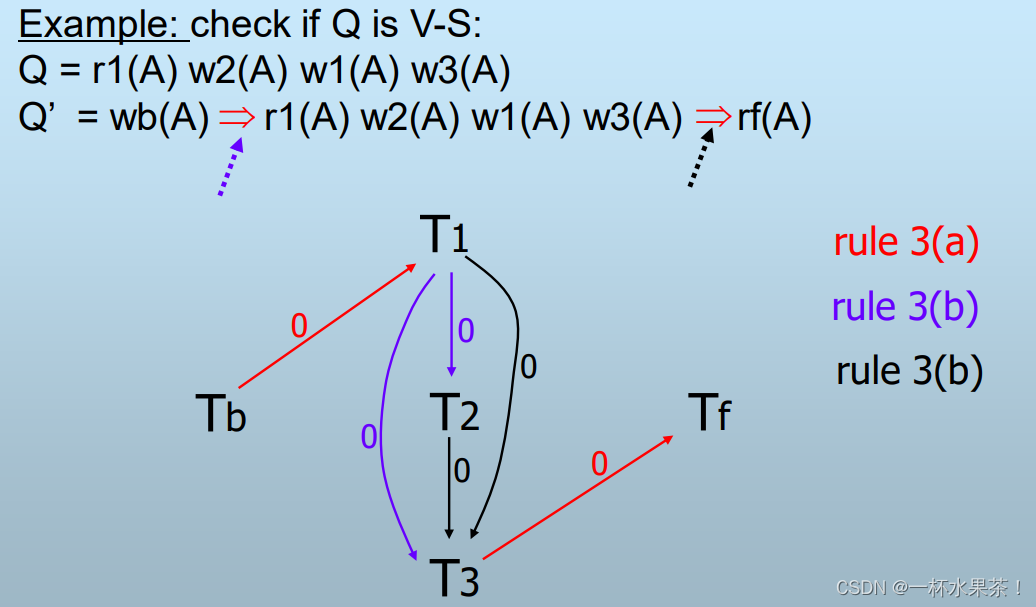
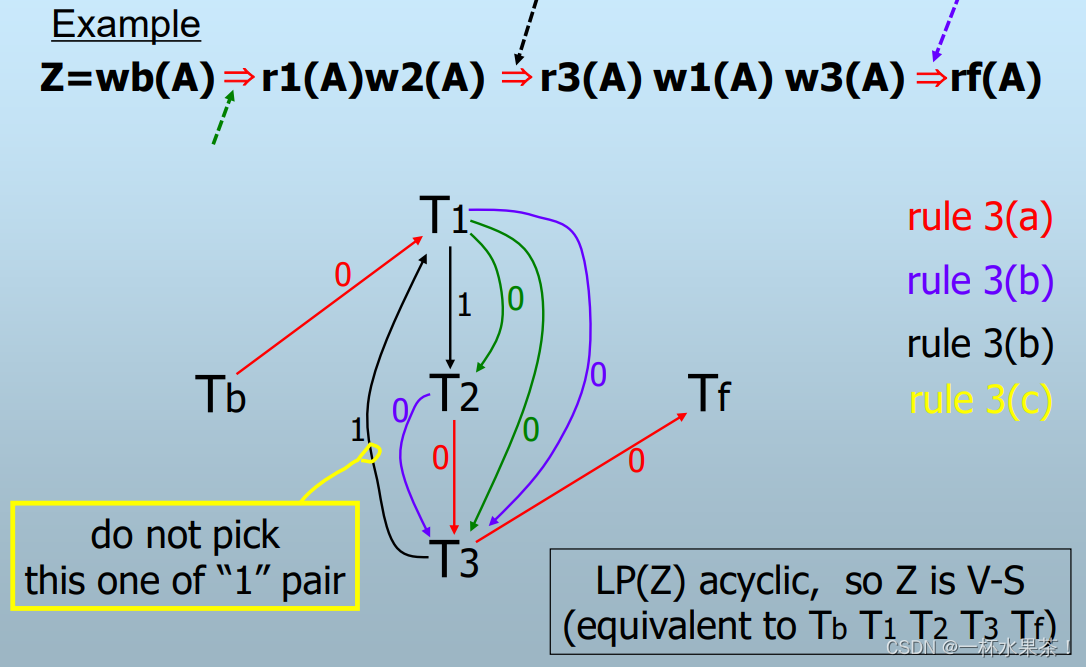
多重图画法步骤:
- 先找出所有的 写->读 操作,注意读的是源头。wb(A)->r1(A),w2(A)->r3(A),w3(A)->rf(A) 这三对如红线所示,注意 wb(A) r3(A) 并不是一对,因为 r3(A) 读的源头是 w2(A) 而不是 wb(A)。
- 再根据上一步找出的 写->读 操作,对每一个 写->读,找出所有其他事务中的写操作,
– 如果写是 wb,如 wb(A)->r1(A),那么除了 wb(A) 以外其他对元素 A 的写操作有 w2(A),w3(A),由于 wb(A)->r1(A) 中 T1 是作为 “接收” 的一方,所以接下来由 T1 “发送” 到其他写的事务,即从 T1->T2,T1->T3。如图中绿色线所示。
– 如果读是 rf,如 w3(A)->rf(A),那么除了 w3(A) 和 wb(A) 以外其他对元素 A 的写操作有 w1(A),w2(A),由于 w3(A)->rf(A) 中 T3 是作为 “发送” 的一方,所以接下来由 T3 “接收” 来自其他写的事务,即从 T1->T3,T2->T3。如图中紫色线所示。
– 如果写不是 wb,读不是 rf,如 w2(A)->r3(A),那么除了 w2(A) 和 wb(A) 以为其他对元素 A 的写操作有 w1(A),w3(A),由于 w2(A)->r3(A) 中 T2 是 “发送” 的一方,所以接下来由 T2 “接收” 来自其他写的事务,即从 T1->T2,注意标号不为 0,为 1。此外 w2(A)->r3(A) 中 T3 是 “接收” 的一方,所以接下来由 T3 “发送” 到其他写的事务,即从 T3->T1,注意标号不为 0,为 1。如图中黑色线所示。