0. 前言

图生成算法是指用于创建模拟图或网络结构的算法，这些算法可以根据特定的规则和概率分布生成具有特定属性的图，用于模拟各种复杂系统，如社交网络、生物网络、交通网络等。传统图生成技术已有数十年历史，并可用作各种应用的基准，但这些技术在生成的图类型上存在限制。这些方法大多数都专注于输出特定的拓扑结构，因此不能简单地模仿给定网络。在本节中，我们将介绍两种经典图生成技术：Erdős–Rényi 模型和小世界 (small-world) 模型。

1. 图生成技术

图生成是生成新图的技术，并且希望所生成的图具有真实世界中图的性质。作为一个研究领域，它为了解图如何工作和演化提供了新思路。它还可以直接应用于数据增强、异常检测、药物发现等领域。我们可以将图生成分为两种类型：一种是模仿给定图生成具有类似性质的逼真图数据 (例如，数据增强)，另一种是目标导向图生成，即创建优化特定指标的图(例如，分子生成)。

2. Erdős–Rényi模型

Erdős–Rényi 模型是最简单、最流行的随机图 (random graph model) 模型，由匈牙利数学家 Paul Erdős 和 Alfréd Rényi 于 1959 年提出，该模型有两个变体： $G(n,p)$ 和 $G(n,M)$。
在 $G(n,p)$ 模型中：给定节点数量和节点连接的概率，尝试随机地将每个节点与其他节点连接起来，以创建最终的图。这意味着存在 $C_2^n$ 种可能的连接。另一种理解概率 $p$ 的方式是将其视为改变网络密度的参数。使用 networkx 库可以直接实现 $G(n,p)$ 模型。

(1) 导入 networkx 库：

import networkx as nx
import matplotlib.pyplot as plt

(2) 使用 nx.erdos_renyi_graph() 函数生成一个有 10 个节点 (n = 10)、边创建概率为 0.5 (p = 0.5) 的图 $G$：

G = nx.erdos_renyi_graph(10, 0.5)

(3) 使用 nx.circular_layout() 函数为生成的节点布局 pos，也可以使用其他布局，但这种布局便于比较不同的 p 值：

pos = nx.circular_layout(G) 

(4) 使用 nx.draw() 以 pos 布局绘制图 $G$：

nx.draw(G, pos=pos)
plt.show()

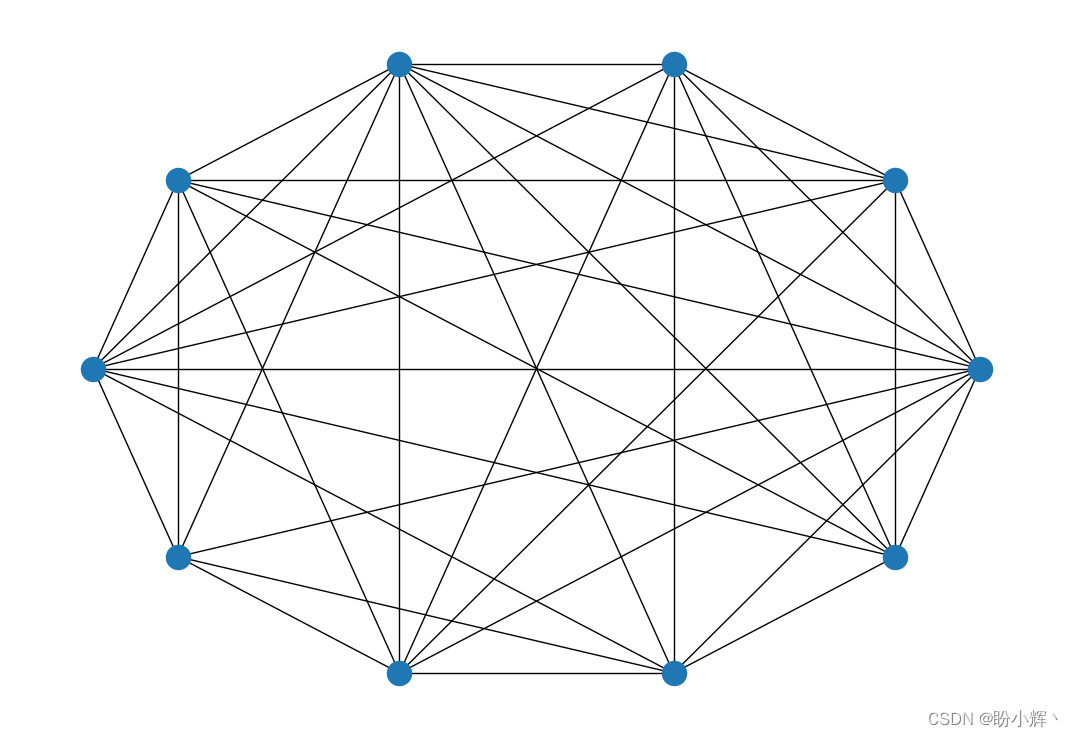
以 0.1 和 0.9 的概率重复以上过程：

G = nx.erdos_renyi_graph(10, 0.1)
pos = nx.circular_layout(G) 
nx.draw(G, pos=pos)
plt.axis('off')
plt.show()

G = nx.erdos_renyi_graph(10, 0.9)
pos = nx.circular_layout(G) 
nx.draw(G, pos=pos)
plt.axis('off')
plt.show()

可以看到，当 $p$ 值较低时，存在许多孤立节点，而当 $p$ 值较高时，图中的节点具有高度互联性。
在 $G(n，M)$ 模型中，从所有具有 $n$ 个节点和 $M$ 条边的图中随机选择一个图。例如，如果 $n=3$，$M=2$，则有三个可能的图，如下图所示，$G(n,M)$ 模型将随机选择其中一个图。这是解决同一问题的不同方法，但通常不如 $G(n,p)$ 模型流行，因为一般情况下它更难以分析：

也可以使用 nx.gnm_random_graph() 函数在 Python 中实现 $G(n,M)$ 模型：

G = nx.gnm_random_graph(3, 2)
pos = nx.circular_layout(G) 
nx.draw(G, pos=pos)
plt.axis('off')
plt.show()

$G(n,p)$ 模型假设链接是独立的，即它们不会相互干扰。然而，对于现实世界中的大多数图而言，这一假设并不成立。

3. 小世界模型

小世界 (small-world) 模型于 1998 年由 Duncan Watts 和 Steven Strogatz 提出，旨在模仿生物和社交网络的行为。其主要思想是，现实世界的网络并非完全随机(如 Erdős–Rényi 模型)，但也并非完全规则(如网格)，通常拓扑结构介于两者之间，因此我们可以使用系数对其进行插值。小世界模型生成的图兼具以下特点：

• 路径短：网络中任意两个节点之间的平均距离相对较小，这使得信息很容易在整个网络中快速传播
• 聚类系数高： 网络中的节点往往彼此紧密相连，形成密集的节点集群

许多算法都具有小世界特性。接下来，我们将介绍最初的 Watts-Strogatz 模型，可以通过以下步骤实现：

1. 初始化一个有 $n$ 个节点的图
2. 每个节点与其 $k$ 个最近的邻居相连(如果 $k$ 为奇数，则与 $k-1$ 个邻居相连)
3. 节点 $i$ 和 $j$ 之间的每个链接在 $i$ 和 $k$ ($k$ 为另一个随机节点)之间重新连接的概率为 $p$

在 Python 中，可以通过调用 nx.watts_strogatz_graph() 函数实现：

G = nx.watts_strogatz_graph(10, 4, 0.5)
pos = nx.circular_layout(G) 
nx.draw(G, pos=pos)
plt.axis('off')
plt.show()

与 Erdős–Rényi 模型一样，可以用不同的概率 $p$ 重复相同的过程：

可以看到，当 $p=0$ 时，图是完全规则的。相反，当 $p=1$ 时，由于每个链接都被重新连接，所以图完全是随机的。通过具有中心节点和局部聚类的平衡图来在这两个极端之间获得一个图。
然而，Watts-Strogatz 模型并不能产生真实的节点度分布。它还需要固定数量的节点，这意味着它不能用于网络的增长。

小结

本节中，介绍了经典的图生成算法，包括 Erdős-Rényi 模型和小世界模型。Erdős-Rényi 模型是最早的随机图模型之一，它根据一定的连接概率在节点之间添加边，从而创建一个随机图。小世界模型通过重连边的方式在规则网络上引入随机性，从而模拟了许多真实世界网络的“小世界”特性，即短路径长度和高聚类系数。并使用 networkx 实现了这两种模型以生成图数据。

系列链接

图神经网络实战（1）——图神经网络(Graph Neural Networks, GNN)基础
图神经网络实战（2）——图论基础
图神经网络实战（3）——基于DeepWalk创建节点表示
图神经网络实战（4）——基于Node2Vec改进嵌入质量
图神经网络实战（5）——常用图数据集
图神经网络实战（6）——使用PyTorch构建图神经网络
图神经网络实战（7）——图卷积网络(Graph Convolutional Network, GCN)详解与实现
图神经网络实战（8）——图注意力网络(Graph Attention Networks, GAT)
图神经网络实战（9）——GraphSAGE详解与实现
图神经网络实战（10）——归纳学习
图神经网络实战（11）——Weisfeiler-Leman测试
图神经网络实战（12）——图同构网络(Graph Isomorphism Network, GIN)
图神经网络实战（13）——经典链接预测算法
图神经网络实战（14）——基于节点嵌入预测链接
图神经网络实战（15）——SEAL链接预测算法