最小权顶点覆盖问题-优先队列分支限界法-C++

news2024/10/5 14:10:40

问题描述:

给定一个赋权无向图 G=(V,E)，每个顶点 v∈V 都有一个权值 w(v)。如果 U⊆V，U⊆V，且对任意(u,v)∈E 有 u∈U 或 v∈U，就称 U 为图 G 的一个顶点覆盖。G 的最小权顶点覆盖是指 G 中所含顶点权之和最小的顶点覆盖。对于给定的无向图 G，设计一个优先队列式分支限界法，计算 G 的最小权顶点覆盖。

算法设计：

为了找到最小权顶点覆盖，这里我们采取优先队列分支限界法来搜索该问题的解空间树。该问题的解空间是一颗子集树，因为对于图中的每一个点，都只有两种选择，加入U集合和不加入U集合，如果扩展开来就会成为一颗二叉树。

要采用优先队列来求解该问题，对于堆中的每一个节点，都有一个目前所选的点的集合，我们需要维护那些已经被选入U集合的点，同时维护当前的点权和，这样每次我们都从堆中选出当前扩展出的节点中点权和最小的一个来扩展，特别的，当点权相同时，我们通过判断当前覆盖集的大小来选择覆盖集大的来扩展。

因为我们采用的是优先队列来查找，我们的目标只是求出一个解，每次从堆中选出的节点都是当前的所有扩展出节点中点权和最小的一个，如果当前节点的状态已经实现了覆盖，那么说明当前已经是最优解了，我们可以直接返回结果。

对于该问题，我们发现无法对每个节点的右儿子进行限界：
因为当右儿子加入U集和时，点权和是不会发生改变的，虽然不加入会让点权和更小，但是不要忽略我们的目标是实现顶点覆盖，我们不扩展右儿子节点就无法保证实现覆盖，所以对右儿子的扩展是必须的。

特别的，在对于当前节点是否覆盖的判断实现中，在这里我们用一个set集合来存储当前U集合顶点可以扩展出的所有节点，这样我们每次查询当前是否覆盖只需要判断set中的元素数目是否等于所有点的数目，这样就可以做到O(1)时间的查询。

对于该问题我们的具体算法流程：
1.读入图的信息，同时初始化优先队列，加入初始的节点。
2.每次从队列中取出当前权值和最小的节点信息，判断是否实现完全覆盖。如果已经是一个完全覆盖集，直接退出搜索，返回结果集。否则需要扩展该结点的左右儿子结点。（对应的，左儿子表示将该结点加入U集合，右儿子代表直接跳过该点）。
3.如果发现当前节点的深度已经大于了节点数目，则说明当前已经搜完所有节点到达了叶子结点，若没有实现完全覆盖则直接退出即可。否则继续进行下一步搜索。

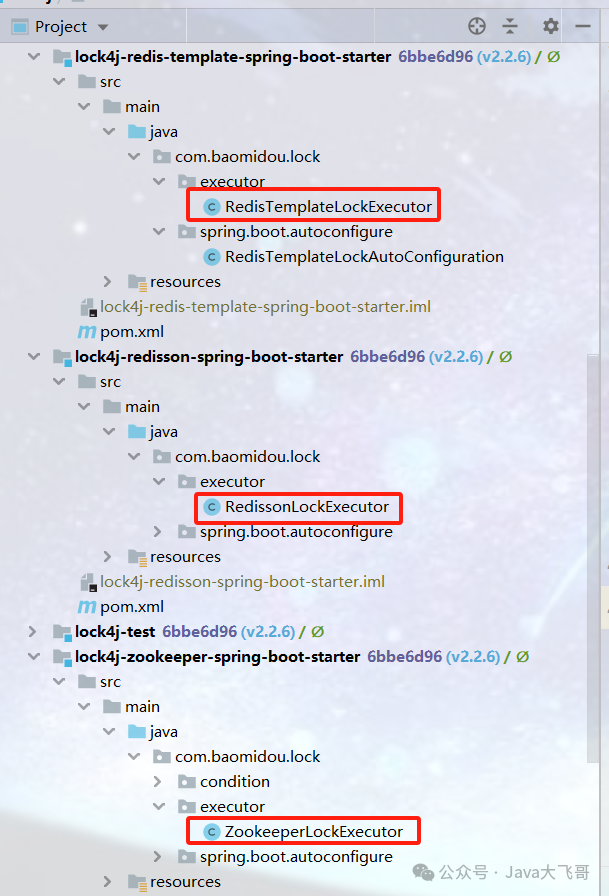
流程图：

在这里插入图片描述

代码：

#include <bits/stdc++.h>
using namespace std;

struct Node {
    int dep; // 深度,第几层就是处理第几个点
    int val; // 权值
    vector<int>U; // U集合
    set<int>st; // 覆盖集

    Node(int dep, int val, vector<int>U, set<int>st):dep(dep), val(val), U(U), st(st) {}
    friend bool operator < (const Node &w1, const Node &w2) {
        if(w1.val == w2.val){
            return w1.st.size() < w2.st.size();
        }
        return w1.val > w2.val;
    }

    friend ostream& operator<<(ostream& os, const Node& p){
        cout << "dep:" << p.dep << " val:" << p.val << " U:";
        for(int i:p.U){
            cout << i << " ";
        }
        cout << " st:";
        for(int i:p.st){
            cout << i << " ";
        }
        return os;
    }
};

struct Whopxx{
    int n;
    vector<int>W; // 点权
    vector<vector<int>>G; // 图
    
    vector<int>bst;
    int bestVal;

    Whopxx(int n,vector<int> w, vector<pair<int,int>> vt):n(n) {
        W = w;
        bst.resize(n + 1);
        G.resize(n + 1);
        for(auto [u, v]:vt){
            G[u].push_back(v);
            G[v].push_back(u);
        }
    }

    void work(){
        priority_queue<Node>q;
        q.push(Node(1, 0, {}, {}));
        while(q.size()){
            Node node = q.top(); q.pop();
            cout << node << endl;
            if(is_cover(node)){ // 当前节点实现全覆盖
                for(int i: node.U){
                    bst[i] = 1;
                }
                bestVal = node.val;
                break;
            }
            if(node.dep > n){ // 搜完叶子结点仍未覆盖
                continue;
            }
            else{
                Node lnode = add(node, node.dep); 
                q.push(lnode); // 左
                
                Node rnode = uadd(node);
                q.push(rnode); // 右
            }
        }
    }

    bool is_cover(Node &node){ // 判断是否为覆盖集
        return node.st.size() == n;
    }
    
    Node add(Node node, int u){ // 加入
        node.U.push_back(u); // 加入U
        node.val += W[u];
        node.dep += 1;
        node.st.insert(u);

        for(auto v: G[u]){
            node.st.insert(v);
        }
        return node;
    }

    Node uadd(Node node){
        node.dep += 1;
        return node;
    }
};

int main(){ 
    freopen("input.txt","r", stdin);
    freopen("output.txt", "w", stdout);

    int n, m;
    cin >> n >> m;
    vector<int>w(n + 1);
    for(int i = 1; i <= n; i++) cin >> w[i];
    vector<pair<int,int>>vt;
    for(int i = 1; i <= m; i++){
        int u, v;cin >> u >> v;
        vt.push_back({u, v});
    }
    Whopxx wx(n, w, vt);
    wx.work();
    cout << wx.bestVal << endl;
    vector<int>ans = wx.bst;
    for(int i = 1;i <= n; i++){
        cout << ans[i] << ' ';
    }

    fclose(stdin);
    fclose(stdout);
    return 0;
}
/*

7 7
1 100 1 1 1 100 10
1 6
2 4
2 5
3 6
4 5
4 6
6 7

5 4
1 100 1 1 1
1 2
3 2
4 2
5 2

4 3
1 100 1 1
1 2
3 2
4 2

4 3
1 3 1 1
1 2
3 2
4 2

4 4
1 2 10 10
1 2
2 3
3 4
4 1

*/