一个认为一切根源都是“自己不够强”的INTJ
![]() 个人主页:用哲学编程-CSDN博客
个人主页:用哲学编程-CSDN博客![]() 专栏:每日一题——举一反三
专栏:每日一题——举一反三
Python编程学习
Python内置函数
Python-3.12.0文档解读
目录
我的写法
时间复杂度分析
空间复杂度分析
总结
哲学和编程思想
1. 抽象与具体化
2. 迭代与递归
3. 分治法
4. 组合数学
5. 优化与效率
6. 模块化与复用
7. 防御性编程
8. 算法复杂度
9. 简洁与清晰
10. 面向对象与函数式编程
总结
举一反三
1. 抽象与模块化
2. 迭代与递归
3. 分治法
4. 组合数学
5. 优化与效率
6. 模块化与复用
7. 防御性编程
8. 算法复杂度
9. 简洁与清晰
10. 面向对象与函数式编程
总结
题目链接:https://pintia.cn/problem-sets/994805260223102976/exam/problems/type/7?problemSetProblemId=1478633632938655744&page=0
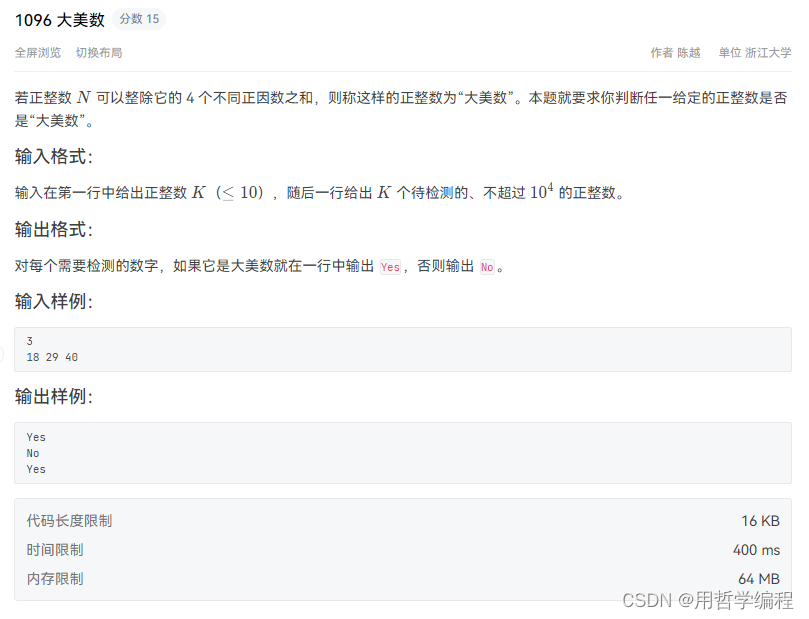
我的写法
import itertools
import math
def factors(num):
# 因数包括1和本身
output = set()
for i in range(1, int(math.sqrt(num)) + 1):
if num % i == 0:
output.add(i)
output.add(num // i)
return output
K = int(input())
nums = list(map(int, input().split()))
for num in nums:
num_factors = factors(num)
#print(num_factors)
if len(num_factors) >= 4:
for combination in itertools.combinations(num_factors, 4):
# 正整数 N 可以整除它的 4 个不同正因数之和,分清谁是除数被除数
if sum(combination) %num == 0:
#print(combination)
print("Yes")
break
else:
print("No")
else:
print("No")
时间复杂度分析
- 因数计算函数 factors(num):
- 该函数的时间复杂度主要由遍历从1到 sqrt(num) 的整数决定,因此是 O(sqrt(num))。
- 主程序逻辑:
- 对于每个正整数 num,计算因数的时间复杂度是 O(sqrt(num))。
- 如果因数集合的长度大于等于4,则需要生成所有可能的4个因数的组合,并检查每个组合的和是否能被 num 整除。
- 生成所有4个因数的组合的时间复杂度是 O(C_n^4),其中 n 是因数的数量。由于 n 通常远小于 num,这个复杂度可以近似为 O(n^4)。
- 因此,对于每个正整数 num,总的时间复杂度是 O(sqrt(num) + n^4)。
空间复杂度分析
- 因数计算函数 factors(num):
- 该函数使用了一个集合来存储因数,因此空间复杂度是 O(sqrt(num))。
- 主程序逻辑:
- 主程序逻辑的空间复杂度主要由存储因数集合 num_factors 决定,因此是 O(sqrt(num))。
- 此外,生成组合时会占用一些额外的空间,但由于组合的数量通常不会太大,这部分空间复杂度可以忽略不计。
总结
- 时间复杂度:对于每个正整数 num,总的时间复杂度是 O(sqrt(num) + n^4)。
- 空间复杂度:总的空间复杂度是 O(sqrt(num))。
这段代码在处理每个正整数时,能够有效地计算因数并检查是否存在满足条件的组合。然而,对于非常大的正整数,生成所有可能的4个因数的组合可能会导致较高的计算成本。
哲学和编程思想
这段代码体现了以下哲学和编程思想:
1. 抽象与具体化
- 抽象:代码通过定义函数 factors(num) 来抽象出计算一个数的所有因数的过程。这种抽象使得代码更模块化,便于理解和维护。
- 具体化:在主程序中,通过调用 factors(num) 函数并结合具体逻辑(如组合生成和条件判断)来解决具体问题。
2. 迭代与递归
- 迭代:代码中使用 for 循环来遍历因数和组合,这是一种迭代思想。迭代通常比递归更直观且效率更高。
3. 分治法
- 分治法:代码通过将问题分解为两个子问题:计算因数和检查组合。这种分治法使得问题更易于管理和解决。
4. 组合数学
- 组合数学:代码使用 itertools.combinations 来生成所有可能的4个因数的组合。这体现了组合数学中的组合生成思想。
5. 优化与效率
- 优化:代码在生成组合时,一旦找到满足条件的组合就立即返回结果,避免了不必要的计算,这是一种优化思想。
- 效率:通过使用集合 set 来存储因数,避免了重复因数,提高了效率。
6. 模块化与复用
- 模块化:代码通过定义独立的函数 factors(num),使得计算因数的过程可以被复用,体现了模块化编程思想。
- 复用:主程序中多次调用 factors(num) 函数,体现了代码复用的原则。
7. 防御性编程
- 防御性编程:代码在检查因数数量时,先判断因数数量是否大于等于4,这是一种防御性编程思想,确保程序在处理边界情况时不会出错。
8. 算法复杂度
- 算法复杂度:代码在计算因数时,通过遍历到 sqrt(num) 来减少计算量,体现了对算法复杂度的考虑。
9. 简洁与清晰
- 简洁:代码通过使用 itertools.combinations 和集合操作,使得代码简洁且易于理解。
- 清晰:代码结构清晰,逻辑明确,易于阅读和维护。
10. 面向对象与函数式编程
- 函数式编程:代码主要采用函数式编程风格,通过定义函数和使用高阶函数(如 itertools.combinations)来解决问题。
- 面向对象:虽然代码主要采用函数式编程风格,但也可以通过将函数封装到类中来实现面向对象编程。
总结
这段代码体现了抽象与具体化、迭代与递归、分治法、组合数学、优化与效率、模块化与复用、防御性编程、算法复杂度、简洁与清晰以及函数式编程等多种哲学和编程思想。这些思想共同构成了代码的设计和实现基础。
举一反三
根据上述哲学和编程思想,以下是一些技巧,可以帮助你举一反三,更好地解决类似问题:
1. 抽象与模块化
- 抽象化问题:将复杂问题分解为更小的、可管理的部分。例如,将计算因数的功能抽象为一个独立的函数。
- 模块化设计:确保每个函数或模块只做一件事,并且做得好。这样可以使代码更易于测试、维护和复用。
2. 迭代与递归
- 选择合适的循环结构:根据问题的性质选择使用 for 循环或 while 循环。通常,已知迭代次数时使用 for 循环,未知次数时使用 while 循环。
- 递归思维:对于可以自然分解为更小子问题的问题,考虑使用递归。但要注意递归的深度和效率。
3. 分治法
- 分解问题:将大问题分解为多个小问题,分别解决每个小问题,然后将结果合并。这有助于简化复杂问题的解决过程。
4. 组合数学
- 利用组合工具:使用 itertools 库中的组合生成工具(如 combinations 和 permutations)来处理需要生成组合或排列的问题。
5. 优化与效率
- 提前终止:在找到满足条件的解后立即返回,避免不必要的计算。
- 选择合适的数据结构:根据问题的需求选择合适的数据结构,如使用集合 set 来避免重复元素。
6. 模块化与复用
- 代码复用:设计可复用的函数和模块,避免重复代码。
- 库的使用:利用现有的库和工具,如 math 和 itertools,来提高开发效率。
7. 防御性编程
- 边界检查:在处理输入数据时,进行必要的边界检查,确保程序在异常情况下也能正常运行。
- 错误处理:使用异常处理机制来捕获和处理可能的错误。
8. 算法复杂度
- 选择合适的算法:根据问题的规模和性质选择合适的算法,考虑时间复杂度和空间复杂度。
- 优化算法:对算法进行优化,减少不必要的计算和存储。
9. 简洁与清晰
- 代码风格:保持代码风格一致,使用有意义的变量名和函数名,使代码易于理解。
- 注释和文档:添加必要的注释和文档,帮助他人理解代码。
10. 面向对象与函数式编程
- 选择编程范式:根据问题的性质选择合适的编程范式。函数式编程适合处理数据转换和计算密集型任务,而面向对象编程适合处理复杂的数据结构和对象交互。
- 混合使用:在必要时,可以将函数式编程和面向对象编程结合起来,发挥各自的优势。
总结
通过运用这些技巧,可以更好地理解和解决类似问题,提高编程能力和代码质量。不断实践和总结经验,将有助于在编程道路上不断进步。