目录
前言
一、什么是遗传算法?
(一)基本结构
(二)遗传操作
二、仿真过程
(一)主程序部分
(二)选择函数
(三)交叉函数
(四)变异函数
(五)仿真结果
总结
前言
遗传算法是经典的智能化优化算法,可以针对非线性约束以及非凸函数进行相应的优化,得到近似的最优解,是科学研究中常用到的算法。该文针对遗传算法的基本思想、结构以及遗传的三个基本操作进行了分析讲解,并结合一个实例进行了仿真实验,读者可以根据仿真代码进行相应的修改,但是需要注意的一点是具体问题中的适应度函数以及参数设计需要自行调整,不同问题具体分析才能获得较好的结果。
一、什么是遗传算法?
遗传算法(genetic algorithm,GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法,该算法属于智能算法,在函数优化等方面具有重要的应用价值。
遗传算法中的一个种群由经过基因编码的一定数目的个体组成,每个个体实际上是染色体带有特征的实体。染色体作为遗传物质的主要载体,即多个基因的集合,其内部表现(即基因型)是某种基因组合,它决定了个体形状的外部表现,如黑头发的特征需要实现从表现型到基因型的映射,即编码工作。由于仿照基因编码的工作很复杂,往往需要进行简化,如二进制演化出越来越好的近似解。在每一代,根据问题域中个体的适应度大小选择行组合交叉和变异。产生出代表新的解集的群中的最优个体经过解码,可以作为问题的近似最优解。
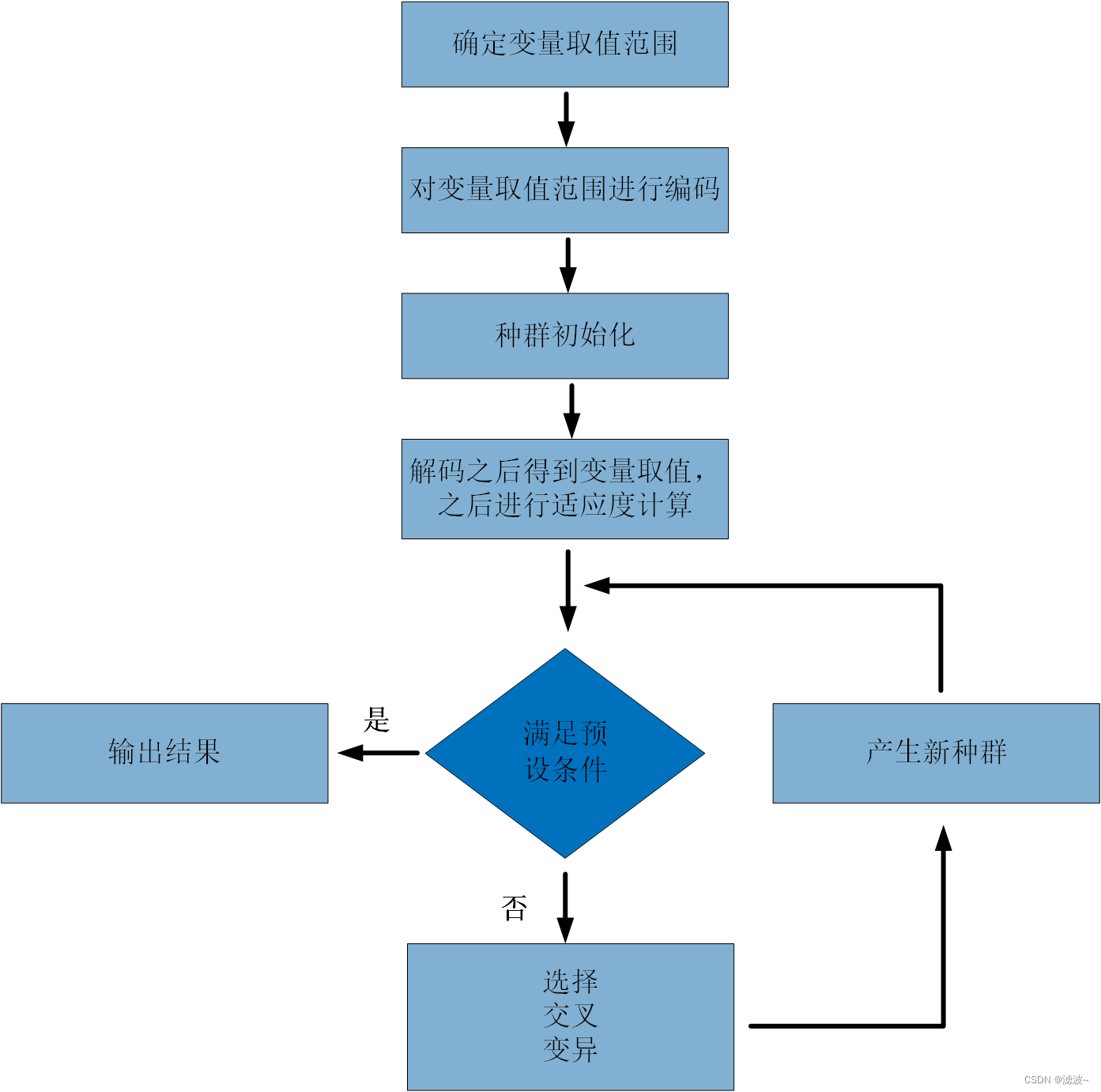
(一)基本结构
人们对遗传算法进行了大量的改进,出现了自适应遗传算法、混合遗传算法等变形算法,但是其基础思想离不开Holland提出的基本算法,我们通常把Holland提出的算法称为基本遗传算法。其基本思想如图所示:
(二)遗传操作
遗传操作包括以下三个:选择、交叉、变异。此外算法中涉及以下设计准则:
(1)种群的规模:种群规模太小时,很明显会出现近亲交配,产生病态基因,而且同时遗传算子存在随机误差(模式采样误差),妨碍小群体中有效模式的正确传播,且浪费资源,稳健性下降。种群规模的一个建议值为0~100。
(2)变异概率:当变异概率太小时,种群的多样性下降太快,容易导致有效基因的迅速丢失且不容易修补;当交异概率太大时,尽管种群的多样性可以得到保证,但是高阶模式迅速被破坏,因此通常选择0.001~0.2。
(3)交配概率:交配是生成新种群最重要的手段。与变异概率类似,交配概率太大容易破坏已有的有利模式,随机性增大,容易错失最优个体;交配概率太小不能有效更新种群。交配概率一般取0.4~0.99。
(4)进化代数:进化代数太小,算法不容易收敛,种群还没有成熟;代数太大,算法已经熟练或者种群过于早熟不可能再收敛,继续进化没有意义,只会增加时间开支和资源浪费。进化代数一般取100~500。
(5)种群初始化:初始种群的生成是随机的;在初始种群赋予之前,尽量进行一个大概的区间估计,以免初始种群分布在远离全局最优解的编码空间,导致遗传算法的搜索范围受到限制,同时也为算法减轻负担。
(6)适应度函数设计:遗传算法中适应度函数会影响选择概率的计算,所以适应度函数的值要取正值。由此可见,将目标函数映射成求最大值形式且函数值非负的适应度函数是必要的。适应度函数的设计主要满足单值、连续、非负、最大化;合理、一致性;计算量小;通用性强的特点。具体应用中适应度函数的设计按照问题本身的要求而定,其直接影响到遗传算法的性能。
二、仿真过程
针对目标函数的优化做以下仿真,对应的函数及变量取值范围如下所示:
代码如下(示例):
(一)主程序部分
clear all;
clc;
global BitLength %全局变量,计算如果满足求解精度至少需要编码的长度
global boundsbegin %全局变量,自变量的起始点
global boundsend %全局变量,自变量的终止点
bounds = [-2, 2]; %一维变量的取值点
precision = 0.01; %运算精度
boundsbegin = bounds(:,1);
boundsend = bounds(:,2); %计算如果蛮子求解精度至少需要多长的染色体
BitLength = ceil(log2(boundsend-boundsbegin)'./precision);
popsize = 100; %初始种群的大小
Generationmax = 100; %最大代数
procssover = 0.8; %交配概率
pmutation = 0.8; %变异概率
population = round(rand(popsize,BitLength)); %初始种群
%计算适应度
[Fitvalue,cumsump] = fitnessfun(population); % 输入群体population;返回适应度Fitvalue和积累概率cumsump
Generation = 1;
while Generation<Generationmax+1
for j = 1:2:popsize %一对一对的群体进行如下操作(变异、交叉)
%选择
seln = selection(population,cumsump);
%交叉
scro = crossover(population,seln,procssover);
scnew(j,:) = scro(1,:);
scnew(j+1,:) = scro(2,:);
%变异
smnew(j,:) = mutation(scnew(j,:),pmutation);
smnew(j+1,:) = mutation(scnew(j+1,:),pmutation);
end
%产生了新的种群
population = smnew;
%计算新种群的适应度
[Fitvalue,cumsump] = fitnessfun(population); % 记录当前代最好的适应度和平均适应度
[fmax,nmax] = max(Fitvalue); %最好的适应的度为fmax(即函数最大值),其对应的个体为nmax
fmean = mean(Fitvalue); %平均适应度为fmean
ymax(Generation) = fmax; %每代中的平均适应度
ymean(Generation) = fmean; %每代中的平均适应度
%记录当前代的最佳染色体个体
x = transform2to10(population(nmax,:)); %population(nma,:)为最佳的染色体个体
xx = boundsbegin + x*(boundsend - boundsbegin)/(power(2,BitLength)-1); %将二进制的值转换为定义域之内的值
xmax(Generation) = xx;
Generation = Generation + 1;
end
Generation = Generation - 1;
targetfunvalue = targetfun(xmax);
[Besttargetfunvalue,nmax] = max(targetfunvalue);
Bestpopulation = xmax(nmax);
%绘制经过遗传运算后的适应度曲线
figure(1);
hand1 = plot(1:Generation,ymax);
set(hand1,'Linestyle','-','Linewidth',1,'marker','*','markersize',8);
hold on;
hand2 = plot(1:Generation,ymean);
set(hand2,'color','k','Linestyle','-','Linewidth',1,'marker','h','markersize',8);
xlabel('进化代数');
ylabel('最大和平均适应度');
xlim([1 Generationmax]);
legend('最大适应度','平均适应度');
box off;
hold off;
(二)选择函数
function seln = selection(population,cumsump)
% 选择两个个体,可能两个个体的序号相同
for i = 1:2
r = rand;
prand = cumsump-r;
j = 1;
while prand(j)<0
j = j +1;
end
seln(i) = j;
end
end(三)交叉函数
function scro = crossover(population,seln,pc)
%新种群交叉操作
BitLength = size(population,2); %二进制数的个数
pcc = IfCroIfMut(pc); % 根据交叉概率决定是否进行交叉操作,1则是,0则否
%进行交叉操作
if pcc == 1
cnb = round(rand*(BitLength-2)) + 1; %随机产生一个交叉位
scro(1,:) = [population(seln(1),1:cnb) population(seln(2),cnb+1:BitLength)];
%序号为sen(1)的个体,在交叉位cnb前面的信息与序号为seln(2)的个体在交叉位cnb+1后面的信息重新组合
scro(2,:) = [population(seln(2),1:cnb) population(seln(1),cnb+1:BitLength)];
%序号为sen(2)的个体,在交叉位cnb前面的信息与序号为seln(1)的个体在交叉位cnb+1后面的信息重新组合
else
%不进行交叉操作
scro(1,:) = population(seln(1),:);
scro(2,:) = population(seln(2),:);
end
end(四)变异函数
function snnew = mutation(snew,pmutation)
% 新种群变异操作
% snew为一个个体
BitLength = size(snew,2);
snnew = snew;
pmm = IfCroIfMut(pmutation);
if pmm==1
cnb = round(rand*(BitLength-1))+1; %在[1 BitLength]范围内随机产生一个变异位
snnew(cnb) = abs(snew(cnb)-1); %将0变为1,将1变为0
end
end
(五)仿真结果
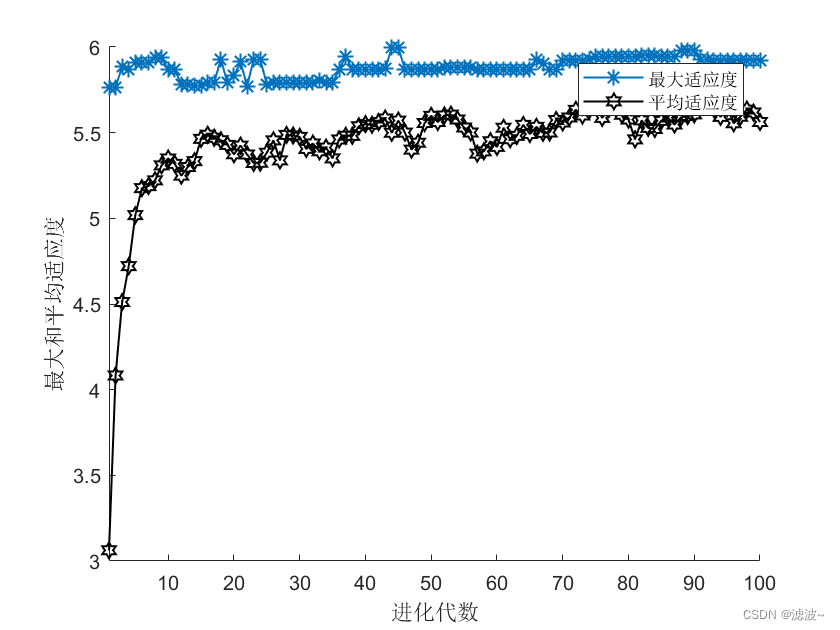
仿真过程中用目标函数作为遗传算法的的适应度函数。从结果中可以看出,随着迭代次数的增加,对应的适应度函数值不断增大,进而目标函数值不断增大,得到函数的最大值。
总结
以上就是今天要讲的内容,本文仅仅简单介绍了遗传算法的思想以及使用,仿真结果表明遗传算法针对优化问题可以获得较好的结果,但是具体问题需要读者进行具体的分析和调参。