一、设计背景

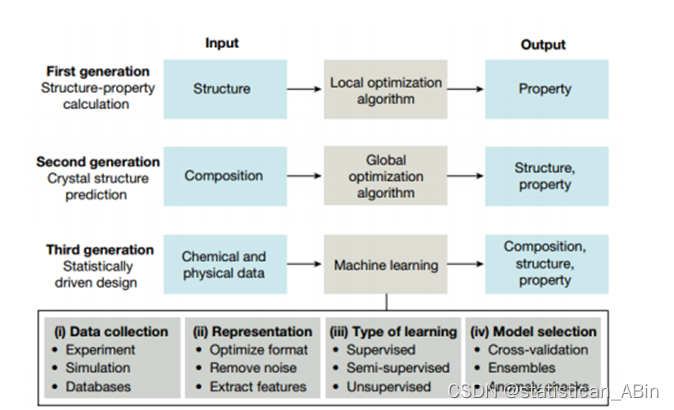
分子结构设计与性质计算对研发新型高能量密度材料具有重要意义。机器学习作为一种大数据计算模型，可以避免复杂、危险的实验，大幅提高研发效率、降低设计和计算成本。本文基于机器学习的方法以及通过构建神经网络，实现对高能量密度化合物的分子设计、性质预测以及高通量筛选。

近来，机器学习在化学与化工生产中的应用也逐渐增多，在化学分子计算方面的应用尤为突出。因为机器学习擅长解决分子计算中化合物分子多、分子空间结构复杂、性质种类多等问题。。。。

二、设计目的和意义

机器学习有助于加速高能量密度化合物的分子设计、性质预测以及新型分子结构的高通量筛选。目前，机器学习和高能量密度化合物相结合的研究依然较少，自主设计公开的相关数据库也不多。直接由高能量密度化合物的分子结构预测其性质仍有很大研究空间。因此，构建高能量密度化合物分子结构-性质关系数据库并实现机器学习辅助数据挖掘具有重要研究意义。 。。。

三、数据探索与分析

EDA的技术手段主要包括：汇总统计、可视化，下面分别做介绍。

 汇总统计是量化的（如均值和方差等），用单个数和数的小集合来捕获数据集的特征，从统计学的观点看，这里所提的汇总统计过程就是对统计量的估计过程。可视化技术能够让人快速吸收大量可视化信息并发现其中的模式，是十分直接且有效的数据探索性分析方法，。。。

四、理论部分

决策树

分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点( node）和有向边( directed edge)组成。结点有两种类型:内部结点( internal node )和叶结点( leaf node )。

多层感知机模型

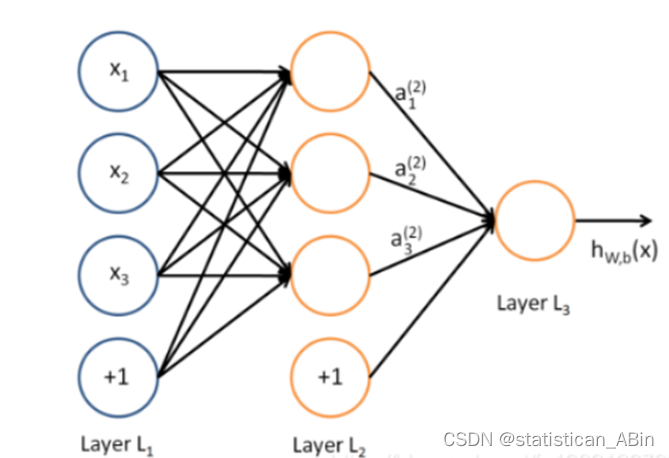
多层感知机（MLP，Multilayer Perceptron）也叫人工神经网络（ANN，Artificial Neural Network），除了输入输出层，它中间可以有多个隐层，最简单的MLP只含一个隐层，即三层的结构，如下图。

向量机模型

支持向量机（support vector machines，SVM）是一种二分类和多分类模型

五、实证分析

首先导入必要的包和数据集，注意这里的数据集是excel格式，而且有两个sheet，随后查看训练集和验证集数据前10行：

代码和数据

报告代码数据

import numpy as np 
import pandas as pd 
import matplotlib.pyplot as plt 
import seaborn as sns 
#引入Excel库的xlrd
import xlrd
import datetime
%matplotlib inline
plt.rcParams['font.sans-serif'] = ['KaiTi']  #中文
plt.rcParams['axes.unicode_minus'] = False   #负号

train_data=pd.read_excel('D:/例题/分子类型预测 for students.xlsx',sheet_name=0)
###查看数据前五行
train_data.head(10)
###由于验证集最后一列没有数据  故先不要
v_data=pd.read_excel('D:/例题/分子类型预测 for students.xlsx',usecols=['formula','C','H','O','N','S','group','AImod','DBE','MZ','OC','HC','SC','NC','NOSC','DBE.C','DBE.O','location','sample'],sheet_name=1)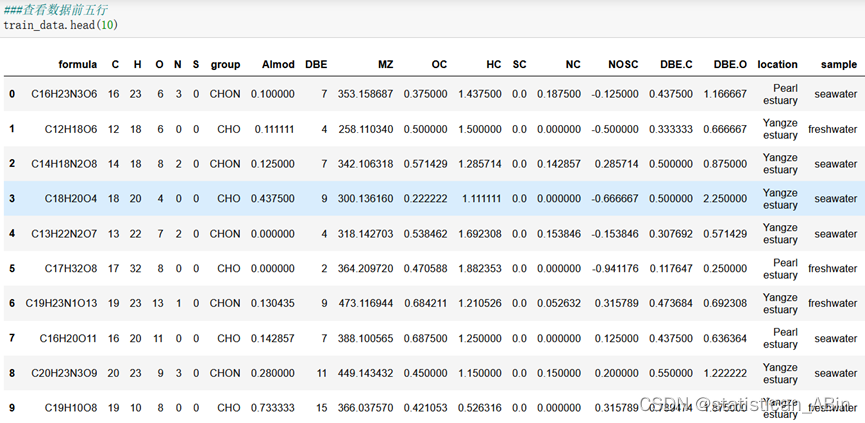

接下来进行训练集和验证集描述性统计分析：

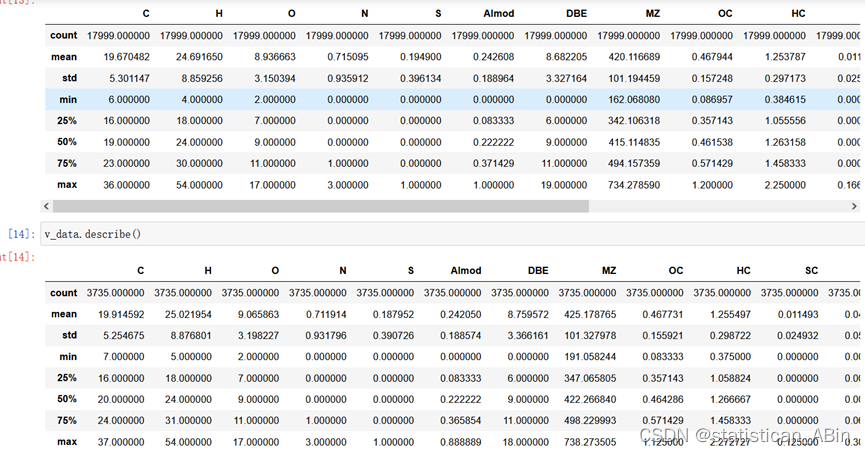
从上可以看出，describe()函数可以展示出数据的总数、最大最小值，均值和标准差以及分位数等等指标。

train_data.describe()
v_data.describe()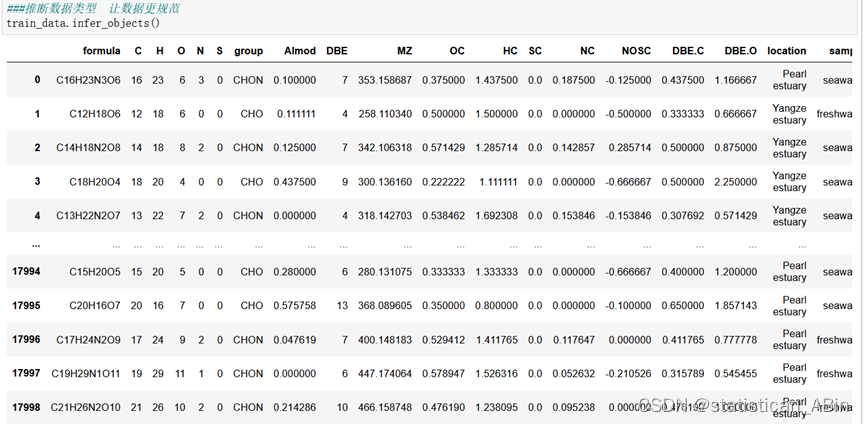

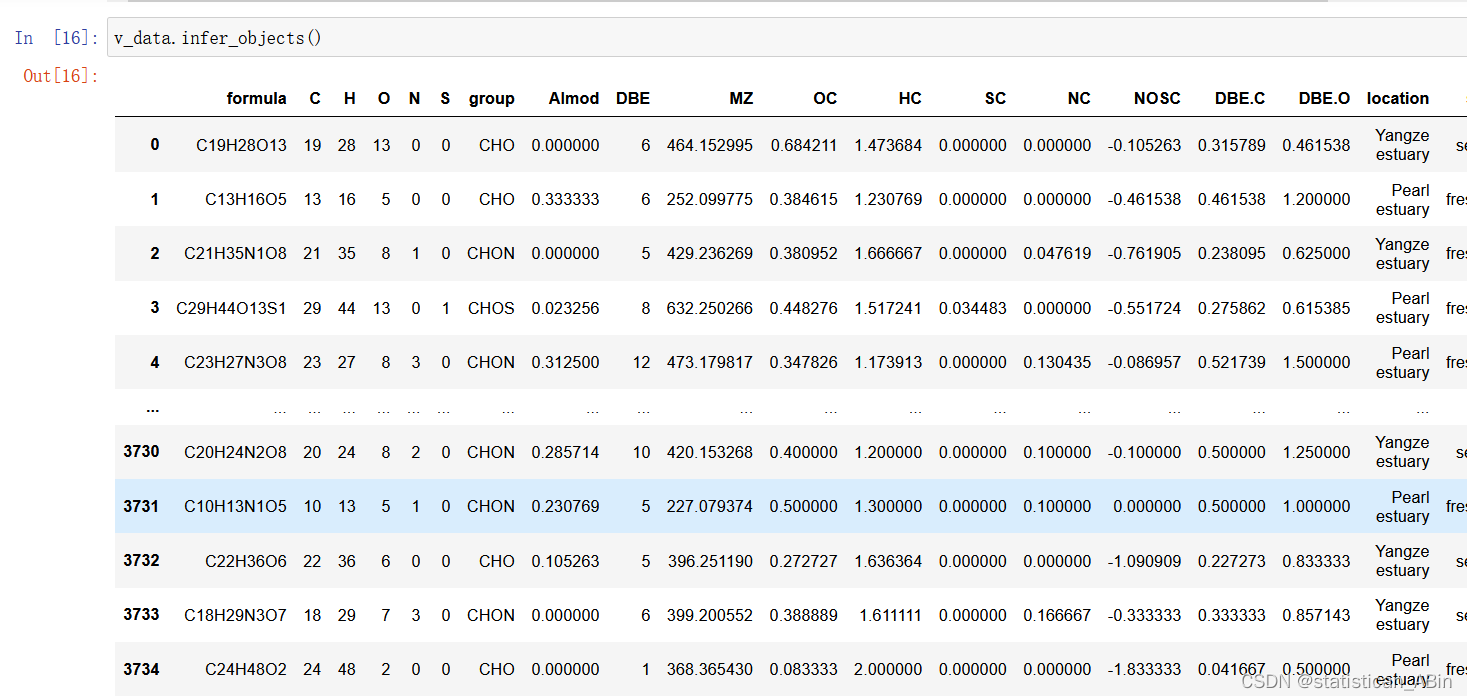
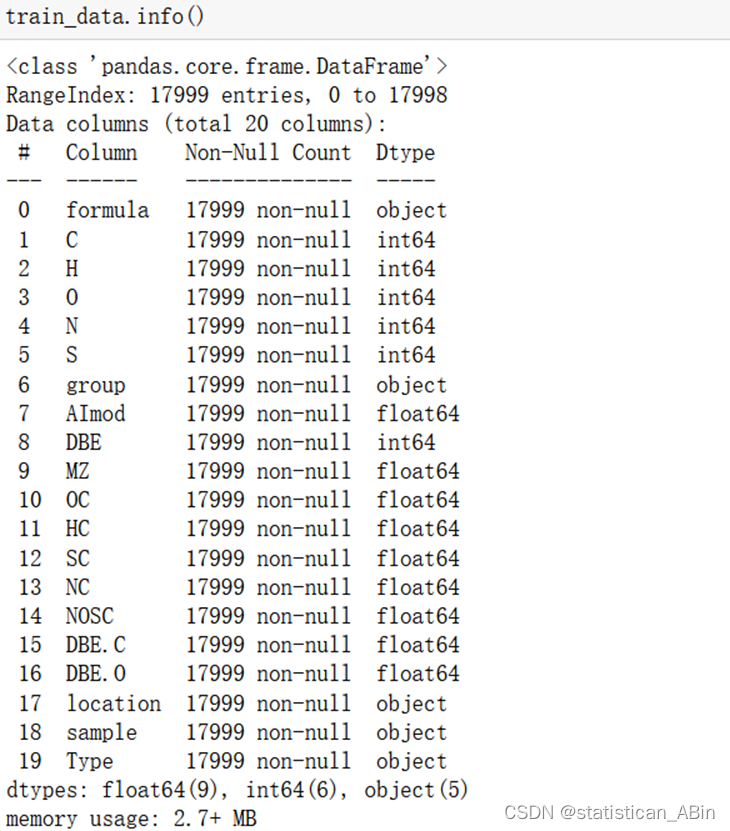
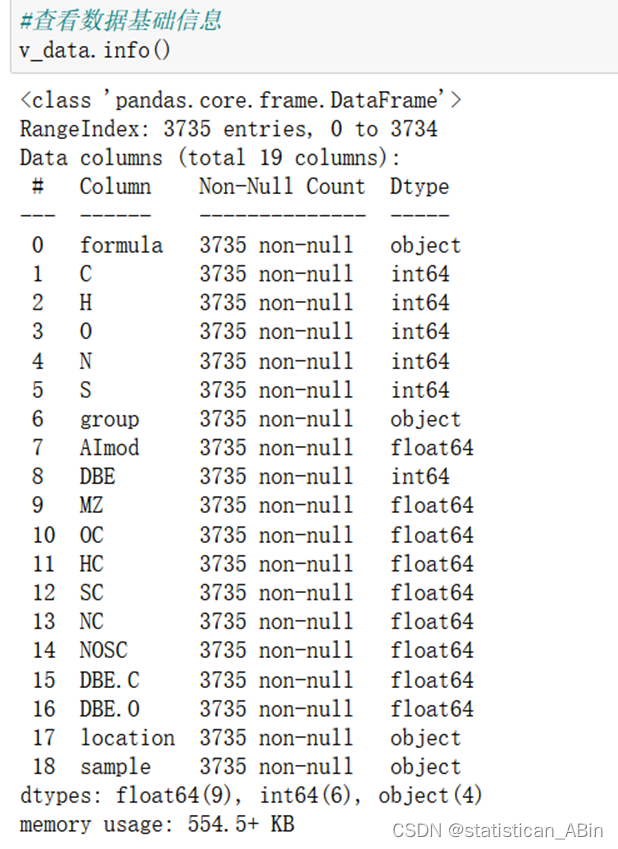
在推断完数据类型之后，分别查看训练集和测试集的数据的不同类型：

 

接下来使用缺失值的可视化函数来查看数据中是否包含缺失值的存在具体结果如下：

 从上面可以看出，无论是训练集还是测试集 数据较为完整，从图上可以看出，每个变量均没有缺失值，故数据较为“干净”，在此验证集v_data不作展示。

进一步数据预处理

所以这里要进行进一步处理，

#删除formula序号
train_data.drop('formula',axis=1,inplace=True)
formula=v_data['formula']

#若是有一行全为空值就删除
train_data.dropna(how='all',inplace=True)
v_data.dropna(how='all',inplace=True)

#取值唯一的变量删除
for col in train_data.columns:
    if len(train_data[col].value_counts())==1:
        print(col)
        train_data.drop(col,axis=1,inplace=True)

miss_ratio=0.15
for col in train_data.columns:
    if  train_data[col].isnull().sum()>train_data.shape[0]*miss_ratio:
        print(col)
        train_data.drop(col,axis=1,inplace=True)

填充缺失值，缺失值有很多填充方式，可以用中位数，均值，众数。也可以就采用那一行前面一个或者后面一个有效值去填充空的(本实验是用均值向前填充)。

train_data.fillna(train_data.median(),inplace=True)   #mode,mean
train_data.fillna(method='ffill',inplace=True)   #pad,bfill/backfill
 
v_data.fillna(v_data.median(),inplace=True)   
v_data.fillna(method='ffill',inplace=True)

独热编码处理其他数据处理：

处理完成之后还可以再次查看数据的情况：

特征变量的箱线图分布情况，查看其是否有离群点：

dis_cols = 7                   #一行几个
dis_rows = len(columns)
plt.figure(figsize=(4 * dis_cols, 4 * dis_rows))
 
for i in range(len(columns)):
    plt.subplot(dis_rows,dis_cols,i+1)
    sns.boxplot(data=train_data[columns[i]], orient="v",width=0.5,palette="Set1")
    plt.xlabel(columns[i],fontsize = 20)
plt.tight_layout()
#plt.savefig('特征变量箱线图',formate='png',dpi=500)
plt.show()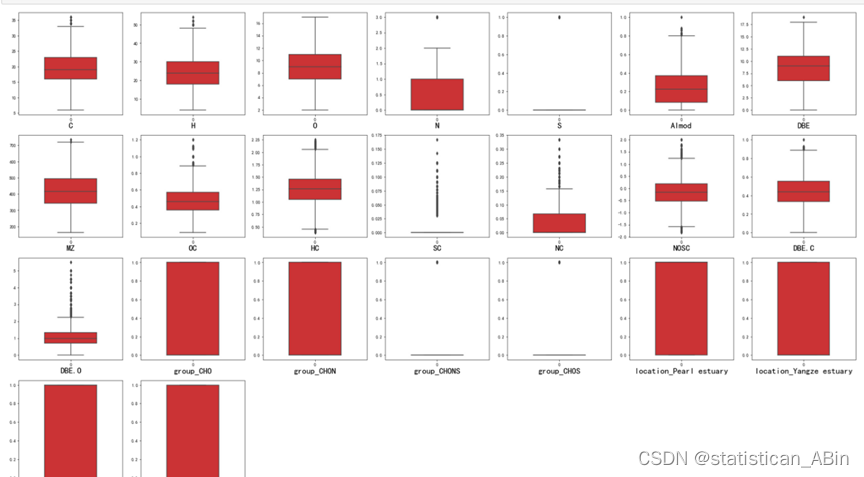

从上面看出，有的特征变量还是存在离群点，比如说SC、NC，后续解决。接下来画出训练集和验证集的特征分布情况。总体上来看，训练集和验证集特征分布较为一致，特征分别较为相识。

plt.figure(figsize=(4 * dis_cols, 4 * dis_rows))
 
for i in range(len(columns)):
    ax = plt.subplot(dis_rows, dis_cols, i+1)
    ax = sns.kdeplot(train_data[columns[i]], color="red" ,shade=True)
    ax = sns.kdeplot(v_data[columns[i]], color="pink",shade=True)
    ax.set_xlabel(columns[i],fontsize = 20)
    ax.set_ylabel("Frequency",fontsize = 18)
    ax = ax.legend(["train", "test"])
plt.tight_layout()
#plt.savefig('训练测试特征变量核密度图',formate='png',dpi=500)
plt.show()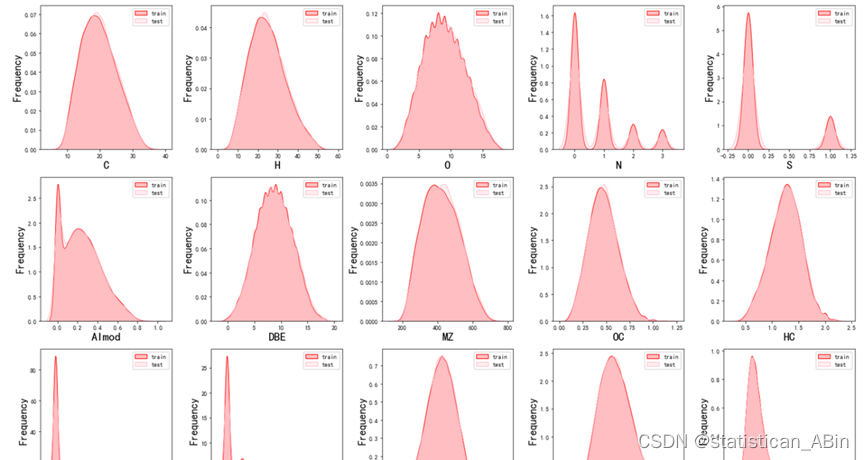

 接下来画出相关系数热力图，故可以从下看出各个特征间的相关系数：

corr = plt.subplots(figsize = (20,16),dpi=128)
corr= sns.heatmap(train_data.assign(Y=y1).corr(method='spearman'),annot=True,cmap="hot",square=True)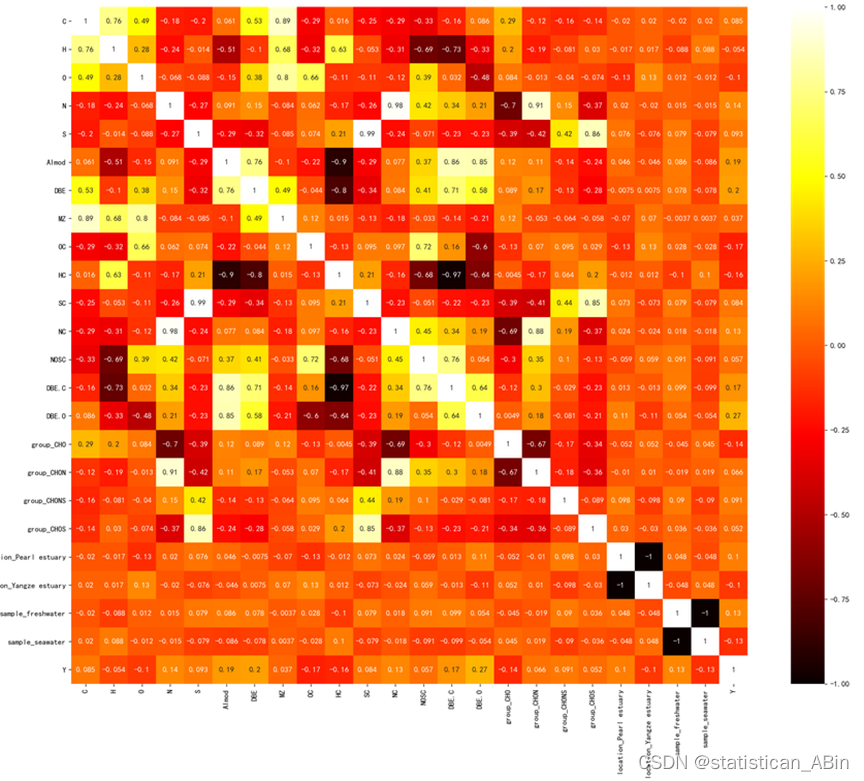

y值分布为：

plt.figure(figsize=(6,2),dpi=128)
plt.subplot(1,3,1)
y1.plot.box(title='响应变量箱线图')
plt.subplot(1,3,2)
y1.plot.hist(title='响应变量直方图')
plt.subplot(1,3,3)
y1.plot.kde(title='响应变量核密度图')
#sns.kdeplot(y, color='Red', shade=True)
#plt.savefig('响应变量.png')
plt.tight_layout()
plt.show()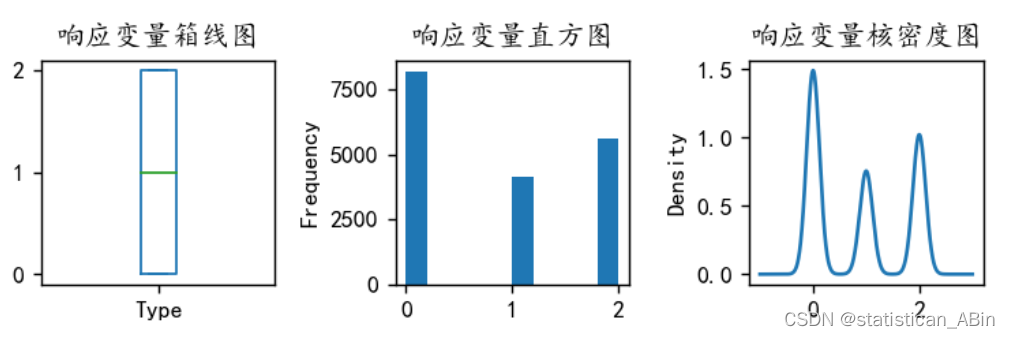

接下来便进入机器学习：

首先划分训练集和验证集，本文的比例是0.2

随后将数据标准化，规范到同一量纲下并查看其形状：

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train_s = scaler.transform(X_train)
X_val_s = scaler.transform(X_val)
X2_s=scaler.transform(v_data)

随后分别采用决策树、MLP和支持向量机进行预测分析，如下：

from sklearn.tree import DecisionTreeClassifier
modelA = DecisionTreeClassifier()
modelA.fit(X_train_s, y_train)
modelA.score(X_val_s, y_val)

#多层感知机MLP
from sklearn.neural_network import MLPClassifier
modelB = MLPClassifier(hidden_layer_sizes=(16,8), random_state=77, max_iter=10000)
modelB.fit(X_train_s, y_train)
modelB.score(X_val_s, y_val)

#支持向量机
from sklearn.svm import SVC
from sklearn.svm import LinearSVC
modelC = SVC(kernel="linear", random_state=123)
modelC.fit(X_val_s, y_val)
modelC.score(X_val_s, y_val)

决策树方法在验证集的准确率为：0.7991666666666667

多层感知机方法在验证集的准确率为：0.8394444444444444

支持向量机方法在验证集的准确率为：0.6713888888888889

从上面可以看出在这3种方法中，多层感知机的预测准确度最高，决策树次之，最后是支持向量机。选择最优模型进行分子类型预测：

随后计算出相应的准确率、精确率、召回率、F1指标

df_eval=pd.DataFrame(columns=['Accuracy','Precision','Recall','F1_score'])
for i in range(3):
    model_C=model_list[i]
    name=model_name[i]
    model_C.fit(X_train_s, y_train)
    pred=model_C.predict(X_val_s)
    s=classification_report(y_val, pred)
    s=evaluation(y_val,pred)
    df_eval.loc[name,:]=list(s)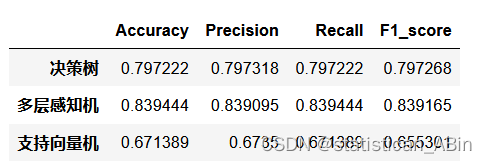

总结与反思

本次大数据分析主要是针对给定的分子数据集，在预处理的基础之上，对不同的分子类型预测等工作，其中使用了两种机器学习模型支持向量机和决策树，使用了一种神经网络模型（多层感知机模型），最终实验发现，多层感知机在分子类型预测准确度表现方面最优，其得分均高于其他两种机器学习模型。

参考文献

1. 侯放. 基于机器学习的高能化合物分子设计与性质预测[D].天津大学,2020.DOI:10.27356/d.cnki.gtjdu.2020.000725.
2. 杨正飞. 基于机器学习的多层次甜味预测系统的构建研究[D].中南林业科技大学,2021.DOI:10.27662/d.cnki.gznlc.2021.000795.  
3. 刘苗. 基于机器学习和分子指纹的化合物hERG心脏毒性预测研究[D].辽宁大学,2021.DOI:10.27209/d.cnki.glniu.2021.001009.
4. 方坚松,庞晓丛,杨然耀,刘艾林,杜冠华. 基于机器学习策略预测抗阿尔滋海默症的小分子与蛋白相互作用[C]//.中国化学会第29届学术年会摘要集——第19分会：化学信息学与化学计量学.[出版者不详],2014:71.

创作不易，希望大家多点赞关注评论！！！（类似代码或报告定制可以私信）