原题链接🔗：二叉树的最近公共祖先
难度：中等⭐️⭐️

题目

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

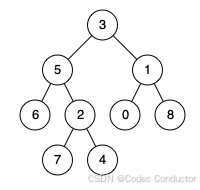
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

• 树中节点数目在范围 [2, 10⁵] 内。
• -10⁹ <= Node.val <= 10⁹
• 所有 Node.val 互不相同 。
• p != q
• p 和 q 均存在于给定的二叉树中。

二叉树最近公共祖先

在二叉树中找到两个节点的最近公共祖先（Lowest Common Ancestor,
LCA）是一个常见的算法问题。最近公共祖先是指在二叉树中，能够同时包含两个给定节点的最低（即最深的）节点。以下是解决这个问题的一般步骤和考虑因素：

• 理解问题：你需要找到两个给定节点在二叉树中的LCA。

• 递归方法：递归是解决这个问题的常用方法。你可以从根节点开始，递归地搜索两个节点。

• 基本情况：

  • 如果当前节点为空，返回空。
  • 如果当前节点等于其中一个给定节点，返回当前节点。

• 递归搜索：

  • 在当前节点的左子树和右子树中递归地搜索两个节点。

• 合并结果：

  • 如果在左子树中找到了一个节点，在右子树中也找到了另一个节点，那么当前节点就是LCA。
  • 如果只在左子树或右子树中找到了一个节点，那么LCA就是这个子树中的节点。
  • 如果两个子树都为空，那么当前节点不是LCA的一部分。

• 实现：使用递归函数实现上述逻辑。

• 测试：确保你的解决方案可以处理各种情况，包括但不限于：

  • 二叉树只有一个节点。
  • 两个节点在不同的分支上。
  • 两个节点在相同的分支上。
  • 两个节点中的一个或两个都是根节点。

• 优化：考虑算法的时间复杂度和空间复杂度。递归方法的时间复杂度通常是O(N)，其中N是树中节点的数量，空间复杂度取决于树的高度，最坏情况下是O(N)。

题解

1. 解题思路：

LeetCode 上的 “二叉树的最近公共祖先 III” 题目要求解决的是在二叉树中找到两个节点的最近公共祖先（LCA）。这个问题可以通过递归的方式来解决，下面是解题的一般思路：

• 定义问题：给定两个值，找到二叉树中包含这两个值的最近公共祖先。

• 理解二叉树：二叉树是一种特殊的树形数据结构，其中每个节点最多有两个子节点。

• 递归方法：

  • 递归函数将接收当前节点和两个值作为参数。
  • 如果当前节点为空，返回空。
  • 检查当前节点是否等于两个值中的任意一个，如果是，返回当前节点。
  • 递归地在左子树和右子树中查找这两个值。

• 处理递归结果：

  • 如果左子树和右子树都为空，说明当前节点的子树中没有找到两个值，返回空。
  • 如果左子树和右子树都非空，说明两个值分别在左右子树中，当前节点就是它们的LCA，返回当前节点。
  • 如果只有一个子树非空，说明两个值都在一个子树中，继续在该子树中查找LCA

2. c++ demo：

#include <iostream>
#include <vector>


struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        // 如果当前节点为空或者等于p或q，返回当前节点
        if (!root || root == p || root == q) {
            return root;
        }

        // 递归地在左子树和右子树中查找p和q
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);

        // 如果左右子树都为空，说明p和q都不在当前节点的子树中
        if (!left && !right) {
            return nullptr;
        }

        // 如果左右子树中只有一个为空，说明p和q都在非空的子树中
        if (left && !right) {
            return left;
        }
        if (!left && right) {
            return right;
        }

        // 如果左右子树都不为空，说明p在一边，q在另一边，当前节点是它们的LCA
        return root;
    }
};

int main() {
    // 构建示例二叉树
    //       2
    //      / \
    //     3   5
    //    / \   \
    //   1   4   6
    TreeNode* root = new TreeNode(2);
    root->left = new TreeNode(3);
    root->right = new TreeNode(5);
    root->left->left = new TreeNode(1);
    root->left->right = new TreeNode(4);
    root->right->right = new TreeNode(6);

    // 创建两个节点
    TreeNode* p = root->left->left; // 值为1的节点
    TreeNode* q = root->right->right; // 值为6的节点

    // 创建Solution对象并调用函数
    Solution solution;
    TreeNode* lca = solution.lowestCommonAncestor(root, p, q);

    // 打印结果
    if (lca) {
        std::cout << "LCA of " << p->val << " and " << q->val << " is " << lca->val << std::endl;
    }
    else {
        std::cout << "No common ancestor found." << std::endl;
    }

    // 清理内存
    delete root->left->left;
    delete root->left->right;
    delete root->right->right;
    delete root->left;
    delete root->right;
    delete root;

    return 0;
}

• 输出结果：

LCA of 1 and 6 is 2