吴恩达机器学习作业ex7:K 均值聚类和主成分分析(Python实现)详细注释

文章目录

1 K 均值聚类
- 1.1 实施 K-means
- - 1.1.1 寻找最近的中心点
  - 1.1.2 计算中心点均值
- 1.2 示例数据集上的 K-means
- 1.3 随机初始化
- 1.4 用 K-means 压缩图像
- - 1.4.1 对像素进行 K 均值分析
2 主成分分析
- 2.1 样例数据集
- 2.3 利用 PCA 降低维度
- - 2.3.1 将数据投影到主成分上
  - 2.3.2 重建数据近似值
  - 2.3.3 预测的可视化
- 2.4 人脸图像数据集
- - 2.4.1 面部 PCA
  - 2.4.2 降维

1 K 均值聚类

在本练习中，您将实现 K-means 算法，并将其用于图像压缩。进行图像压缩。首先，您将从一个示例二维数据集开始。
将帮助你直观地了解 K-means 算法的工作原理。之后，您将使用 K-means 算法进行图像压缩，将图像中出现的颜色数量减少到该图像中最常见的颜色。这部分练习将使用 ex7.m。

1.1 实施 K-means

K-means 算法是一种将相似数据自动聚类的方法。具体来说，你会得到一个训练集 {x (1)，…，x(m)（其中 x(i) ∈ Rⁿ），并希望将这些数据归为几个有凝聚力的 “簇”。K-means 算法背后的直觉是一个迭代过程，首先猜测初始中心点，然后通过反复将示例分配到最接近的中心点来完善这一猜测，然后根据分配结果重新计算中心点。K-means 算法如下：
在这里插入图片描述
算法的内循环重复执行两个步骤： (i) 将每个训练实例 x
(i) 分配给最接近的中心点，以及 (ii) 利用分配给每个中心点的点重新计算其均值。请注意，收敛后的解决方案不一定总是理想的，它取决于中心点的初始设置。因此，在实践中，K-means 算法通常会在不同的随机初始化下运行几次。在这些来自不同随机初始化的不同解决方案中进行选择的一种方法是，选择成本函数值（失真度）最低的解决方案。在接下来的章节中，您将分别实现 K-means 算法的两个阶段。

1.1.1 寻找最近的中心点

在 K-means 算法的 "聚类分配 "阶段，该算法会根据当前中心点的位置，将每个训练实例 x(i) 分配给与其最接近的中心点。具体来说，对于每个实例 i，我们设置
在这里插入图片描述
其中，c(i) 是最接近 x(i) 的中心点的索引，µj 是第 j 个中心点的位置（值）。您的任务是完成 findClosestCentroids.m 中的代码。该函数接收数据矩阵 X 和中心点内部所有中心点的位置，并输出一个一维数组 idx，该数组保存第 1 个中心点的索引（{1, … , K} 中的一个值）。完成 findClosestCentroids.m 中的代码后，脚本 ex7.m 将运行您的代码，您将看到与前 3 个示例的中心点分配相对应的输出 [1 3 2]。

%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat

def findClosestCentroids(X, centroids):
    """
    输出一个一维数组 idx，包含每个训练示例最近的质心的索引。

    参数:
    X -- 训练数据，形状为 (m, n)，其中 m 是样本数量，n 是特征数量。
    centroids -- 质心，形状为 (K, n)，其中 K 是质心数量，n 是特征数量。

    返回:
    idx -- 一维数组，长度为 m，包含每个训练示例最近的质心的索引。
    """
    idx = []  # 用于存储每个训练示例最近质心的索引
    max_dist = 1000000  # 设置一个初始的最大距离，用于比较

    # 遍历每个训练示例
    for i in range(len(X)):
        # 计算当前示例与所有质心的差值，这里使用 NumPy 的广播功能
        minus = X[i] - centroids  
        
        # 计算每个差值的平方和，即欧氏距离的平方
        dist = minus[:, 0]**2 + minus[:, 1]**2
        
        # 如果当前示例与最近质心的距离小于最大距离
        if dist.min() < max_dist:
            # 找到距离最近的质心的索引
            ci = np.argmin(dist)
            # 将该索引添加到 idx 列表中
            idx.append(ci)
    
    # 将 idx 列表转换为 NumPy 数组并返回
    return np.array(idx)

# 加载数据集
mat = loadmat('data/ex7data2.mat')
# 数据集包含 'X' 键，对应的值是一个二维数组
X = mat['X']

# 初始化质心
init_centroids = np.array([[3, 3], [6, 2], [8, 5]])
# 找到每个样本点最近的质心
idx = findClosestCentroids(X, init_centroids)

# 输出前 3 个样本点最近的质心的索引
print(idx[0:3])

1.1.2 计算中心点均值

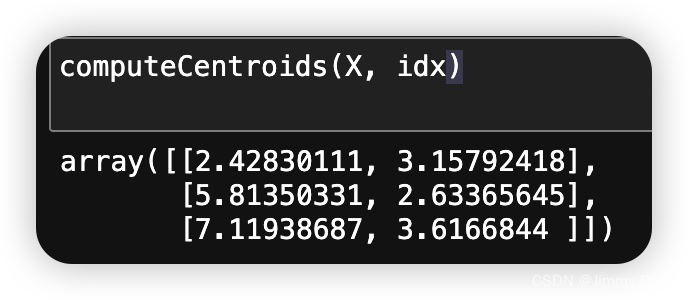
在将每个点分配给一个中心点后，算法的第二阶段将重新计算每个中心点的平均值。具体来说，对于每个中心点 k，我们设置
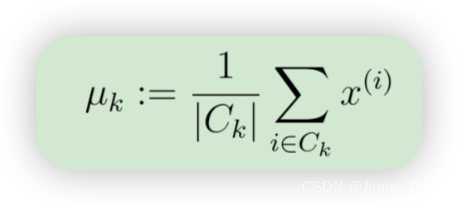
在这里插入图片描述

def computeCentroids(X, idx):
    """
    计算新的质心位置
    Args:
    X : array_like, shape (m, n)
        样本数据，包含 m 个样本，每个样本有 n 个特征。
    idx : array_like, shape (m,)
        样本所属质心的索引，包含 m 个元素，每个元素是一个质心的索引。
        
    Returns:
    centroids : array_like, shape (K, n)
        新的质心位置，包含 K 个质心，每个质心有 n 个特征。
    """
    centroids = []
    for i in range(len(np.unique(idx))):  # np.unique() 返回唯一值的数量，即 K
        u_k = X[idx==i].mean(axis=0)  # 求每列的平均值
        centroids.append(u_k)
        
    return np.array(centroids)

在这里插入图片描述

1.2 示例数据集上的 K-means

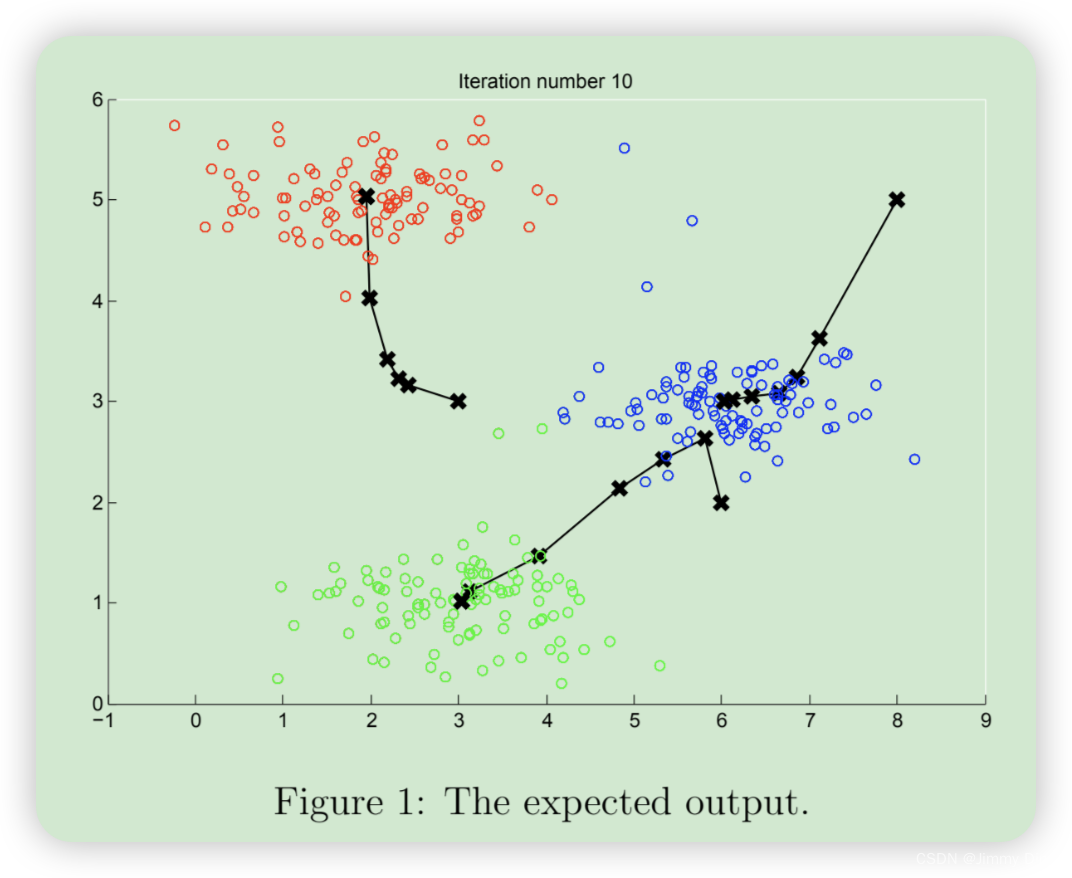
在这里插入图片描述

完成这两个函数（findClosestCentroids 和computeCentroids）后，ex7.m 的下一步将在一个二维数据集上运行 K-means 算法，以帮助您理解 K-means 的工作原理。您的函数将在 runKmeans.m 脚本中调用。我们建议您查看一下函数，以了解其工作原理。请注意，在一个循环中调用了您实现的两个函数。当你运行下一步时，K-means 代码会生成一个可视化界面，引导你了解算法在每次迭代时的进展情况。多次按回车键，查看 K-means 算法的每一步是如何改变中心点和聚类分配的。最后，您的图表应该如图 1 所示。


def plotData(X, centroids, idx=None):
    """
    可视化数据，并自动分开着色。
    
    参数:
    X : array_like, shape (m, n)
        样本数据，包含 m 个样本，每个样本有 n 个特征。
    centroids : list of array_like, shape (k, n)
        包含每次迭代中质心位置的历史记录，每个质心有 n 个特征。
    idx : array_like, shape (m,), optional
        样本所属质心的索引，包含 m 个元素，每个元素是一个质心的索引。如果提供，将按照索引分开着色。
    """
    # 定义颜色列表，用于不同簇的着色
    colors = ['b', 'g', 'gold', 'darkorange', 'salmon', 'olivedrab', 
              'maroon', 'navy', 'sienna', 'tomato', 'lightgray', 'gainsboro',
              'coral', 'aliceblue', 'dimgray', 'mintcream', 'mintcream']
    
    # 确保颜色数量足够用于所有的簇，否则抛出断言错误
    assert len(centroids[0]) <= len(colors), 'colors not enough'
    
    # 初始化子集列表 subX
    subX = []
    if idx is not None:
        # 如果提供了 idx，按照簇索引将样本点分组
        # range(centroids[0].shape[0]) 返回一个从 0 到 centroids[0].shape[0] - 1 的整数序列
        for i in range(centroids[0].shape[0]):
            # 选出属于第 i 个簇的所有样本点，条件是 idx == i
            x_i = X[idx == i]
            # 将这些样本点添加到 subX 列表中
            subX.append(x_i)
    else:
        # 如果没有提供 idx，将 X 转化为一个元素的列表
        subX = [X]  # subX 是一个包含所有样本点的列表
    
    # 创建一个图形并设置尺寸
    plt.figure(figsize=(8, 5))    
    # 分别画出每个簇的样本点，并用不同的颜色表示
    for i in range(len(subX)):
        xx = subX[i]
        # 绘制散点图，颜色由 colors[i] 指定，标签为 'Cluster %d' % i
        plt.scatter(xx[:, 0], xx[:, 1], c=colors[i], label='Cluster %d' % i)
    # 添加图例
    plt.legend()
    # 显示网格
    plt.grid(True)
    # 设置 x 轴标签
    plt.xlabel('x1', fontsize=14)
    # 设置 y 轴标签
    plt.ylabel('x2', fontsize=14)
    # 设置图形标题
    plt.title('Plot of X Points', fontsize=16)
    
    # 初始化质心轨迹的 x 和 y 坐标列表
    xx, yy = [], []
    for centroid in centroids:
        # 将质心的 x 坐标添加到 xx 列表
        xx.append(centroid[:, 0])
        # 将质心的 y 坐标添加到 yy 列表
        yy.append(centroid[:, 1])
    
    # 绘制质心的移动轨迹，用红色 'rx--' 标记，并用虚线连接
    plt.plot(xx, yy, 'rx--', markersize=8)
    
# 测试函数
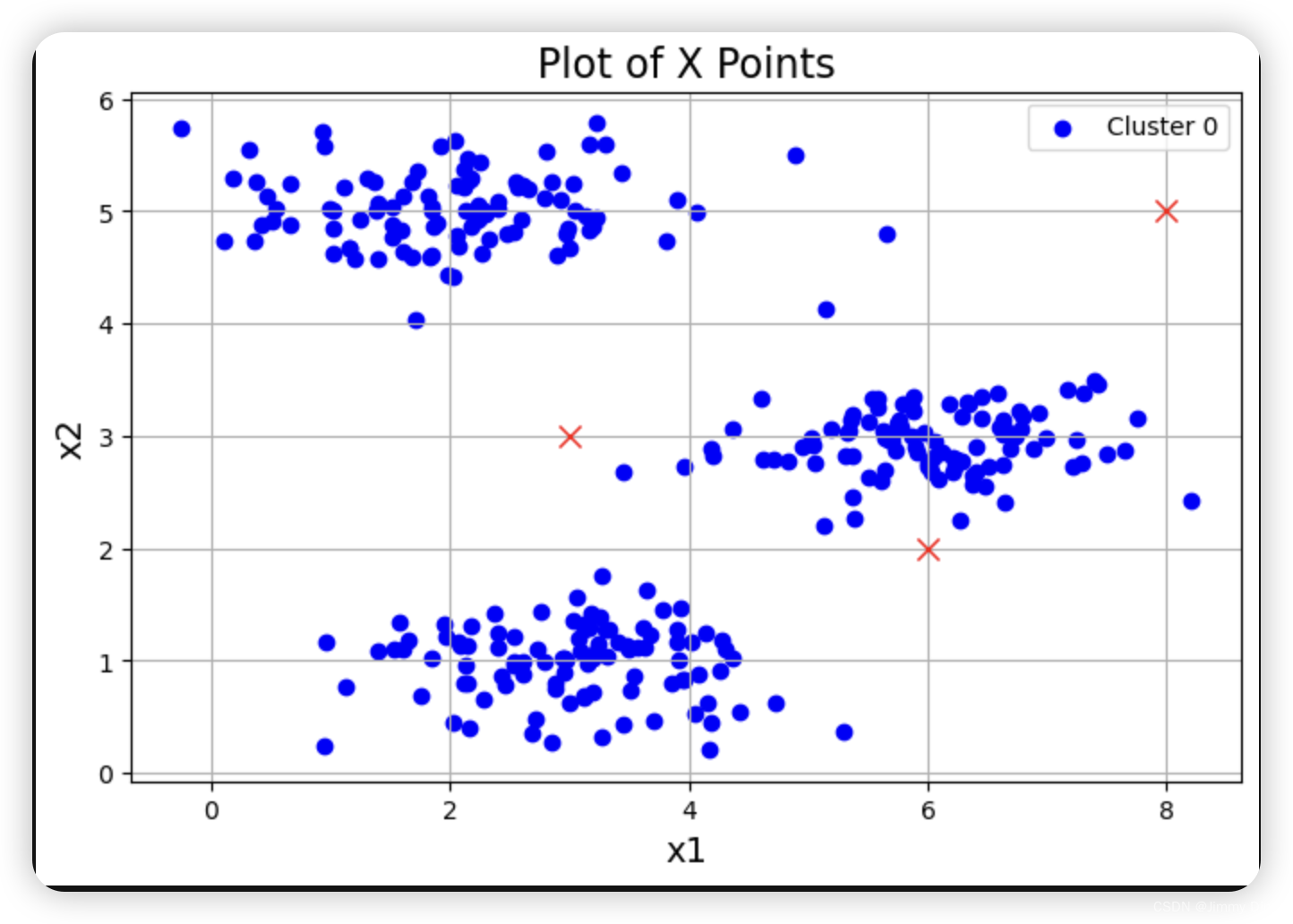
plotData(X, [init_centroids])

在这里插入图片描述

def runKmeans(X, centroids, max_iters):
    """
    运行 K-Means 算法
    
    参数:
    X -- 输入数据矩阵，每行是一个样本点
    centroids -- 初始化的簇中心
    max_iters -- 最大迭代次数
    
    返回:
    idx -- 每个样本点所属的簇的索引
    centroids_all -- 每次迭代后的簇中心点
    """
    # K 是簇的数量
    K = len(centroids)
    
    # 用于存储每次迭代的簇中心点
    centroids_all = []
    centroids_all.append(centroids)
    
    # 当前的簇中心点
    centroid_i = centroids
    
    # 进行 max_iters 次迭代
    for i in range(max_iters):
        # 找到每个样本点最近的簇中心点，得到每个样本点的簇索引
        idx = findClosestCentroids(X, centroid_i)
        
        # 计算新的簇中心点
        centroid_i = computeCentroids(X, idx)
        
        # 存储新的簇中心点
        centroids_all.append(centroid_i)
    
    return idx, centroids_all

# 运行 K-Means 算法
idx, centroids_all = runKmeans(X, init_centroids, 20)

# 可视化结果
plotData(X, centroids_all, idx)

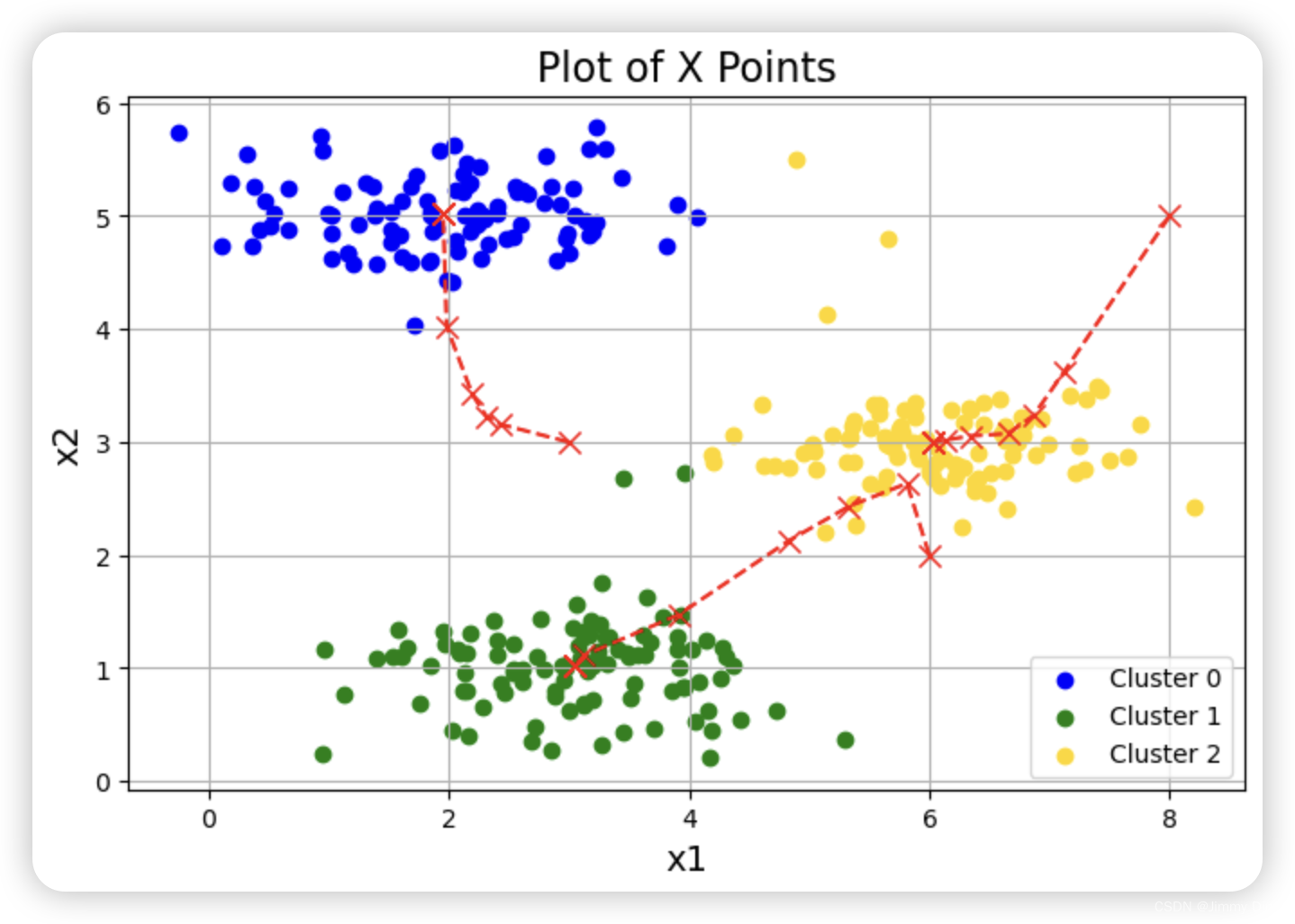
在这里插入图片描述

1.3 随机初始化

我们设计了 ex7.m 中示例数据集的中心点初始分配，以便您能看到与图 1 相同的图形。实际上，初始化中心点的好方法是从训练集中随机选择示例。

def initCentroids(X, K):
    """
    随机初始化簇中心点
    
    参数:
    X -- 输入数据矩阵，每行是一个样本点
    K -- 簇的数量
    
    返回:
    centroids -- 随机初始化的 K 个簇中心点
    """
    m, n = X.shape  # 获取数据矩阵的行数和列数
    idx = np.random.choice(m, K)  # 从 m 个样本点中随机选择 K 个索引
    centroids = X[idx]  # 根据随机选择的索引获取对应的样本点作为初始簇中心点
    
    return centroids  # 返回初始化的簇中心点

# 进行 3 次不同的随机初始化和 K-Means 聚类
for i in range(3):
    centroids = initCentroids(X, 3)  # 随机初始化 3 个簇中心点
    idx, centroids_all = runKmeans(X, centroids, 10)  # 运行 K-Means 算法，迭代 10 次
    plotData(X, centroids_all, idx)  # 可视化结果

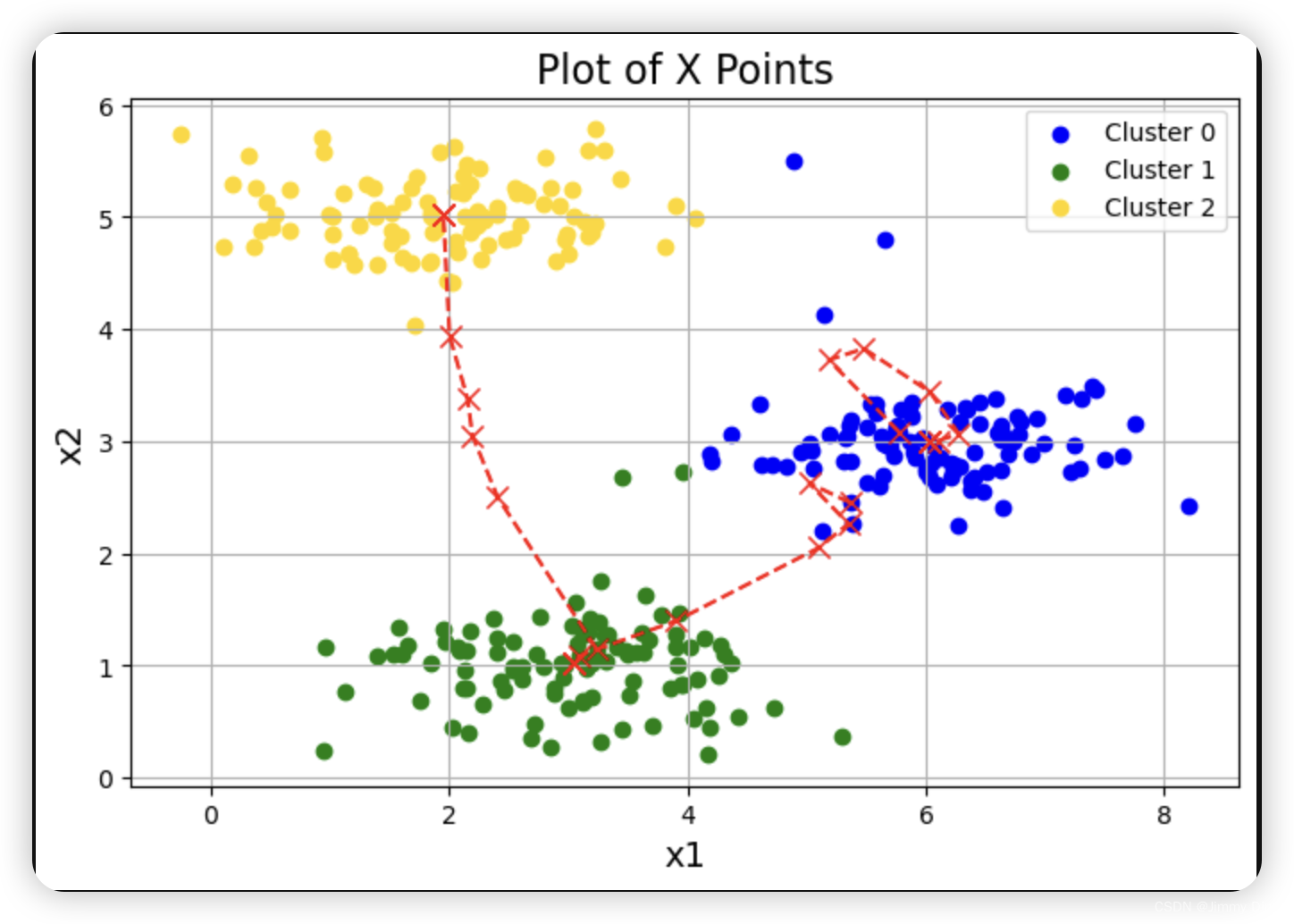
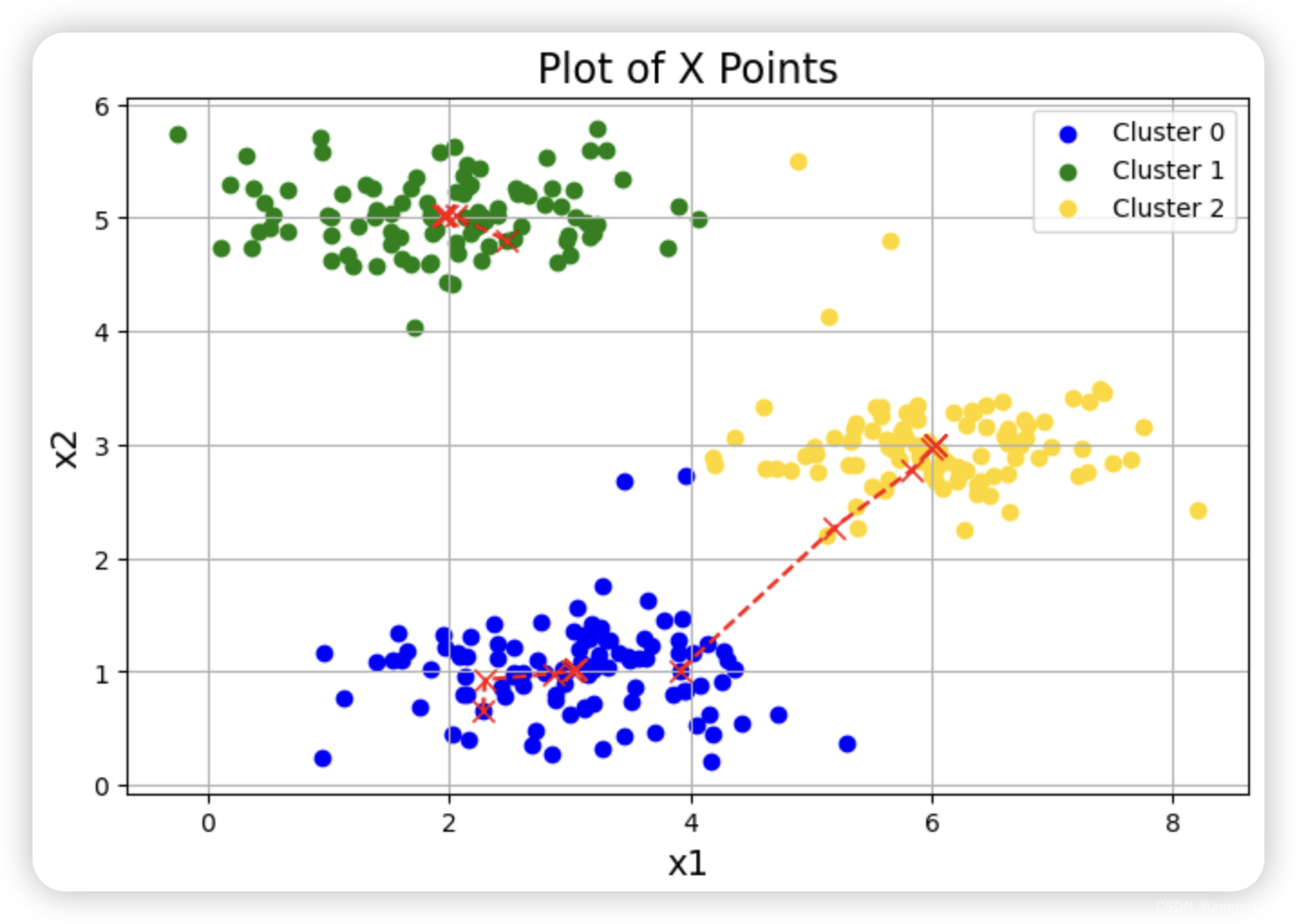
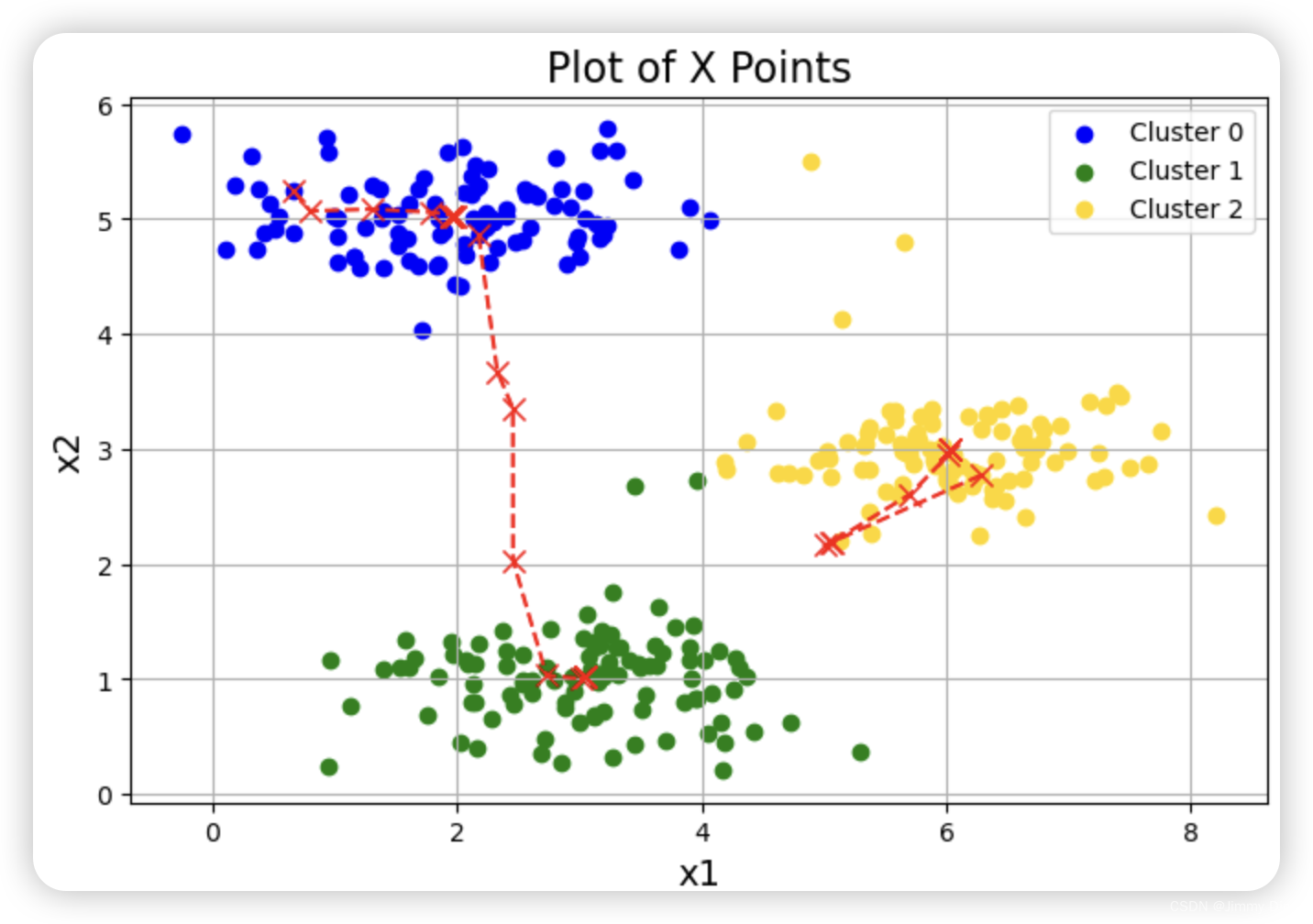
在这里插入图片描述

1.4 用 K-means 压缩图像

在本练习中，您将把 K 均值法应用于图像压缩。在直接的 24比特彩色图像表示法2 中，每个像素表示为三个 8 比特无符号整数（范围从 0 到 255），其中指定了红、绿和蓝的强度值。这种编码通常称为 RGB 编码。我们的图像包含数千种颜色，在本部分练习中，您将把颜色数量减少到 16 种。具体来说，您只需存储所选 16 种颜色的 RGB 值，而对于图像中的每个像素，您现在只需存储该位置的颜色索引（只需 4 个比特来表示 16 种可能的颜色）。在本练习中，您将使用 K-means 算法来选择用于表示压缩图像的 16 种颜色。具体来说，您将把原始图像中的每个像素都视为一个数据示例，并使用 K-means 算法找出在三维 RGB 空间中最能对像素进行分组（聚类）的 16 种颜色。计算出图像的聚类中心点后，就可以使用这 16 种颜色替换原始图像中的像素。

from skimage import io

# 读取图片数据
A = io.imread('/Users/jimmyding/code project/machine learning/Coursera-ML-AndrewNg-Notes/code/ex7-kmeans and PCA/data/bird_small.png')
print(A.shape)

# 显示图片
plt.imshow(A)

# 将图片数据归一化到 0 - 1 的范围
A = A / 255.0

在这里插入图片描述

1.4.1 对像素进行 K 均值分析

这将创建一个三维矩阵 A，其前两个索引表示像素位置，最后一个索引表示红色、绿色或蓝色。例如，A(50, 33, 3) 表示第 50 行第 33 列像素的蓝色强度。ex7.m 中的代码首先加载图像，然后重塑图像以创建一个 m × 3 的像素颜色矩阵（其中 m = 16384 = 128 × 128），并调用 K-means 函数。使用 findClosestCentroids 函数将每个像素位置分配给其最接近的中心点。这样就可以使用每个像素的中心点赋值来表示原始图像。请注意，您已经大大减少了描述图像所需的位数。原始图像的每个 128×128 像素位置需要 24 比特，因此总大小为 128 × 128 × 24 = 393,216 比特。新的表示方法需要存储一些开销，如 16 种颜色的字典，每种颜色需要 24 比特，但图像本身每个像素位置只需要 4 比特。因此，最终使用的比特数为 16 × 24 + 128 × 128 × 4 = 65,920 比特，相当于将原始图像压缩了约 6 倍。
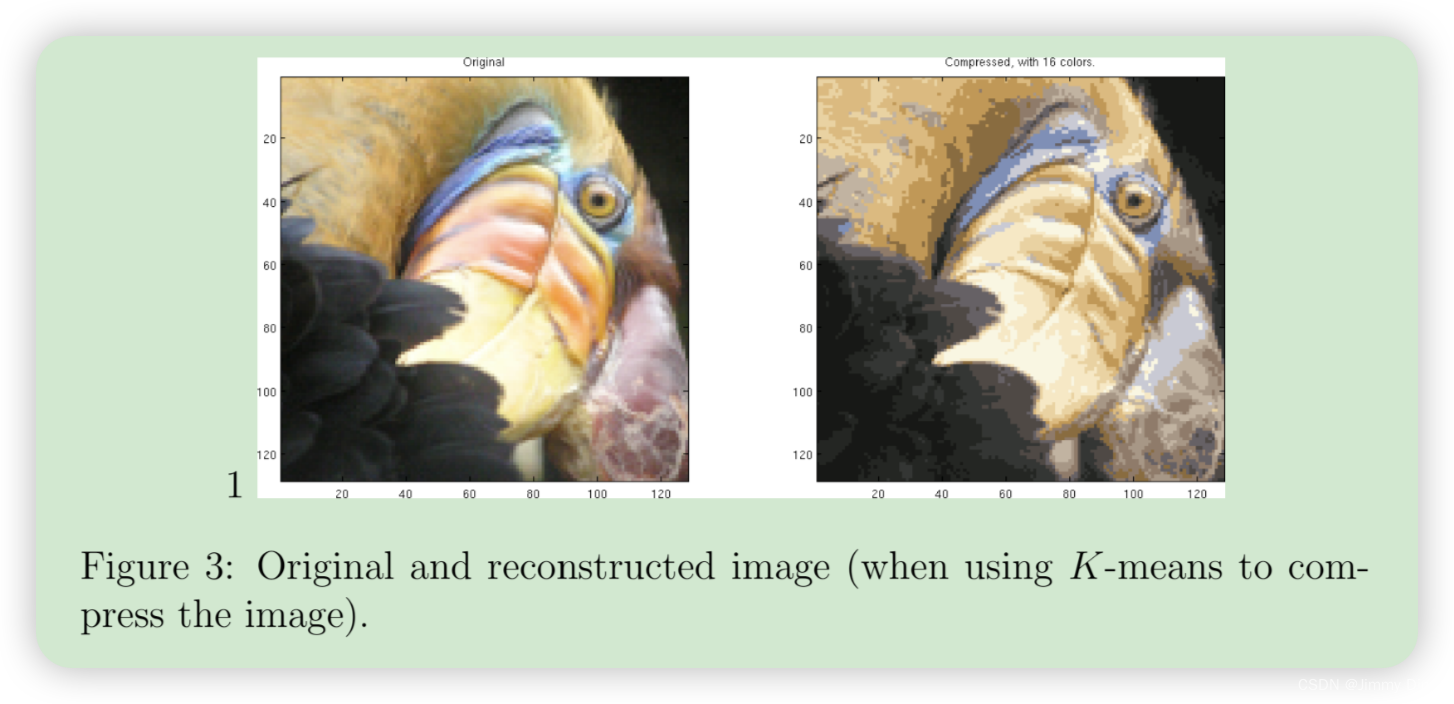
在这里插入图片描述
最后，您可以仅根据中心点分配来重建图像，从而查看压缩的效果。具体来说，您可以用分配给每个像素的中心点的平均值来替换该像素的位置。图 3 显示了我们得到的重建结果。尽管重建后的图像保留了原始图像的大部分特征，但我们也看到了一些压缩伪影。

# 将图像重新塑形为(N, 3)的矩阵，每行表示一个像素的RGB值
X = A.reshape(-1, 3)
K = 16  # 设置K值为16
centroids = initCentroids(X, K)  # 初始化质心
idx, centroids_all = runKmeans(X, centroids, 10)  # 运行K-Means算法

# 初始化一个与原图像相同形状的空数组
img = np.zeros(X.shape)

# 获取最后一次迭代的质心
centroids = centroids_all[-1]

# 将每个像素替换为其对应簇的质心颜色
for i in range(len(centroids)):
    img[idx == i] = centroids[i]

# 将压缩后的图像重新塑形为原图像的尺寸
img = img.reshape((128, 128, 3))

# 创建子图并显示原图像和压缩后的图像
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
axes[0].imshow(A)  # 显示原图像
axes[1].imshow(img)  # 显示压缩后的图像
plt.show()

在这里插入图片描述

2 主成分分析

2.1 样例数据集

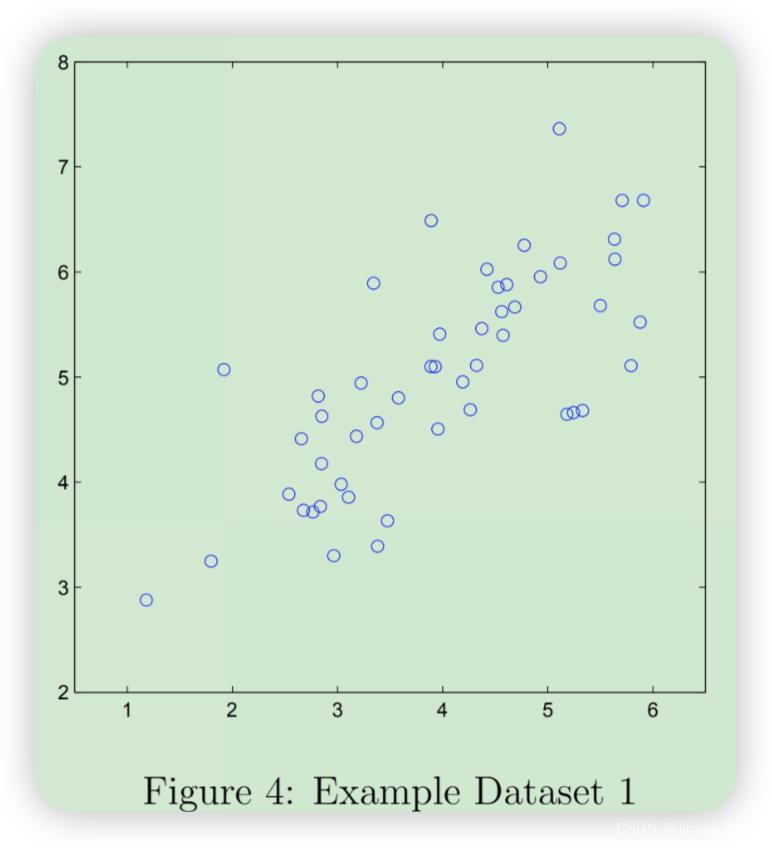
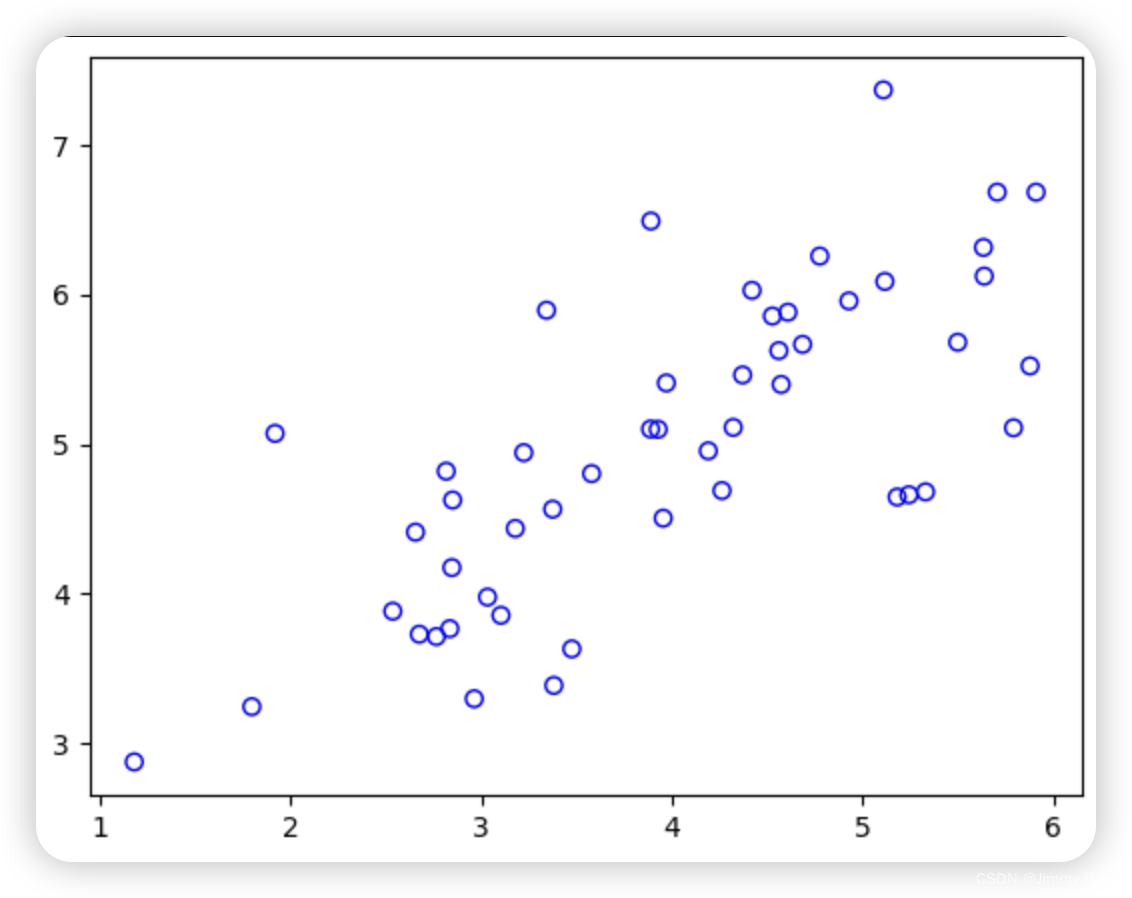
为了帮助您理解 PCA 的工作原理，您将首先从一个二维数据集开始，该数据集的一个方向变化较大，另一个方向变化较小。脚本 ex7 pca.m 将绘制训练数据（图 4）。在这部分练习中，您将直观地看到使用 PCA 将数据从二维还原为一维时发生的情况。在实践中，您可能希望将数据从 256 维减少到 50 维；但在本例中使用低维数据可以让我们更好地可视化算法。
在这里插入图片描述

# 从MAT文件中读取数据
mat = loadmat('data/ex7data1.mat')
X = mat['X']  # 提取数据

# 打印数据的形状
print(X.shape)  # 输出数据的维度，例如(50, 2)，表示有50个样本，每个样本有2个特征

# 绘制散点图
plt.scatter(X[:, 0], X[:, 1], facecolors='none', edgecolors='b')
# X[:, 0] 表示第1列的数据，X[:, 1] 表示第2列的数据
# facecolors='none' 表示点的内部为空心
# edgecolors='b' 表示点的边缘颜色为蓝色
plt.xlabel('X1')  # 设置x轴标签
plt.ylabel('X2')  # 设置y轴标签
plt.title('Scatter plot of X1 vs X2')  # 设置图表标题
plt.grid(True)  # 显示网格
plt.show()  # 显示图表

在这里插入图片描述
在使用 PCA 之前，首先要对数据进行归一化处理，即从数据集中减去每个特征的平均值，并对每个维度进行缩放，使它们处于相同的范围内。在提供的脚本 ex7 pca.m 中，已使用 featureNormalize 函数为您执行了这一归一化操作。对数据进行归一化处理后，就可以运行 PCA 计算主成分了。您的任务是完成 pca.m 中的代码，计算数据集的主成分。首先，您应该计算数据的协方差矩阵，其值为
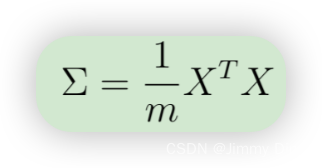
在这里插入图片描述
其中，X 是数据矩阵，行中包含示例，m 是示例个数。注意，Σ 是一个 n × n 矩阵，而不是求和算子。请注意，Σ 是 n × n 矩阵，而不是求和算子。
计算协方差矩阵后，可以运行 SVD 计算主成分。您可以使用以下命令运行 SVD： [U, S, V] = svd(Sigma)，其中 U 将包含主成分，S 将包含对角矩阵。
在这里插入图片描述

def featureNormalize(X):
    """
    对输入数据进行特征归一化。
    
    参数:
    X -- 输入数据，形状为 (m, n)，其中 m 是样本数，n 是特征数。
    
    返回:
    X_norm -- 归一化后的数据，形状与 X 相同。
    means -- 每个特征的均值，形状为 (n, )。
    stds -- 每个特征的标准差，形状为 (n, )。
    """
    
    # 计算每个特征的均值
    means = X.mean(axis=0)  # means 形状为 (n, )
    
    # 计算每个特征的标准差
    stds = X.std(axis=0, ddof=1)  # stds 形状为 (n, )
    
    # 进行特征归一化
    X_norm = (X - means) / stds  # X_norm 形状为 (m, n)
    
    return X_norm, means, stds

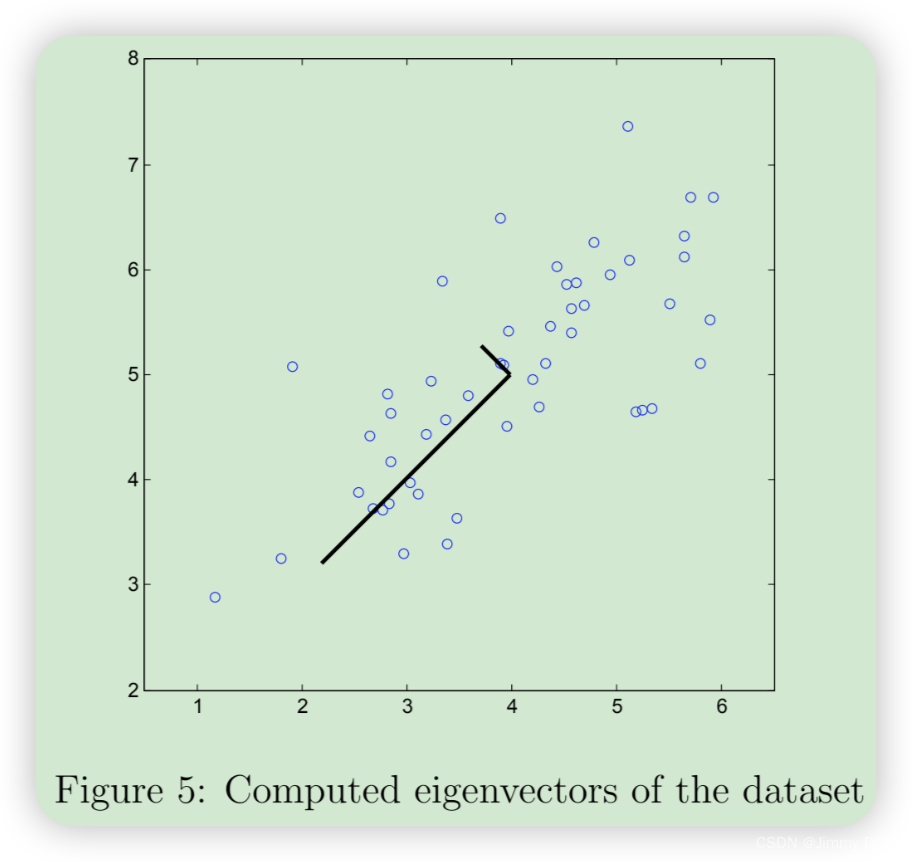
完成 pca.m 后，ex7 pca.m 脚本将在示例数据集上运行 PCA，并绘制出找到的相应主成分（图 5）。该脚本还将输出找到的最高主成分（特征向量），预计输出结果约为 [-0.707-0.707]。(Octave/MATLAB可能会输出负值，因为 U1 和 -U1 同样可以作为第一主成分）。

def pca(X):
    """
    对输入数据进行主成分分析（PCA），计算协方差矩阵，并返回其奇异值分解结果。
    
    参数:
    X -- 输入数据，形状为 (m, n)，其中 m 是样本数，n 是特征数。
    
    返回:
    U -- 左奇异向量矩阵
    S -- 奇异值数组
    V -- 右奇异向量矩阵
    """
    # 计算协方差矩阵
    sigma = (X.T @ X) / len(X)  # sigma 形状为 (n, n)
    
    # 对协方差矩阵进行奇异值分解
    U, S, V = np.linalg.svd(sigma)
    
    return U, S, V

# 对数据进行特征归一化
X_norm, means, stds = featureNormalize(X)

# 对归一化后的数据进行PCA
U, S, V = pca(X_norm)

# 打印第一个主成分
print(U[:,0]) 

# 可视化数据及其主成分
plt.figure(figsize=(7, 5))
plt.scatter(X[:,0], X[:,1], facecolors='none', edgecolors='b')

# 绘制第一个主成分
plt.plot([means[0], means[0] + 1.5*S[0]*U[0,0]], 
         [means[1], means[1] + 1.5*S[0]*U[0,1]],
        c='r', linewidth=3, label='First Principal Component')

# 绘制第二个主成分
plt.plot([means[0], means[0] + 1.5*S[1]*U[1,0]], 
         [means[1], means[1] + 1.5*S[1]*U[1,1]],
        c='g', linewidth=3, label='Second Principal Component')

plt.grid()

# 改变x轴和y轴的限制，以便x和y的增量相等
plt.axis("equal")  
plt.legend()

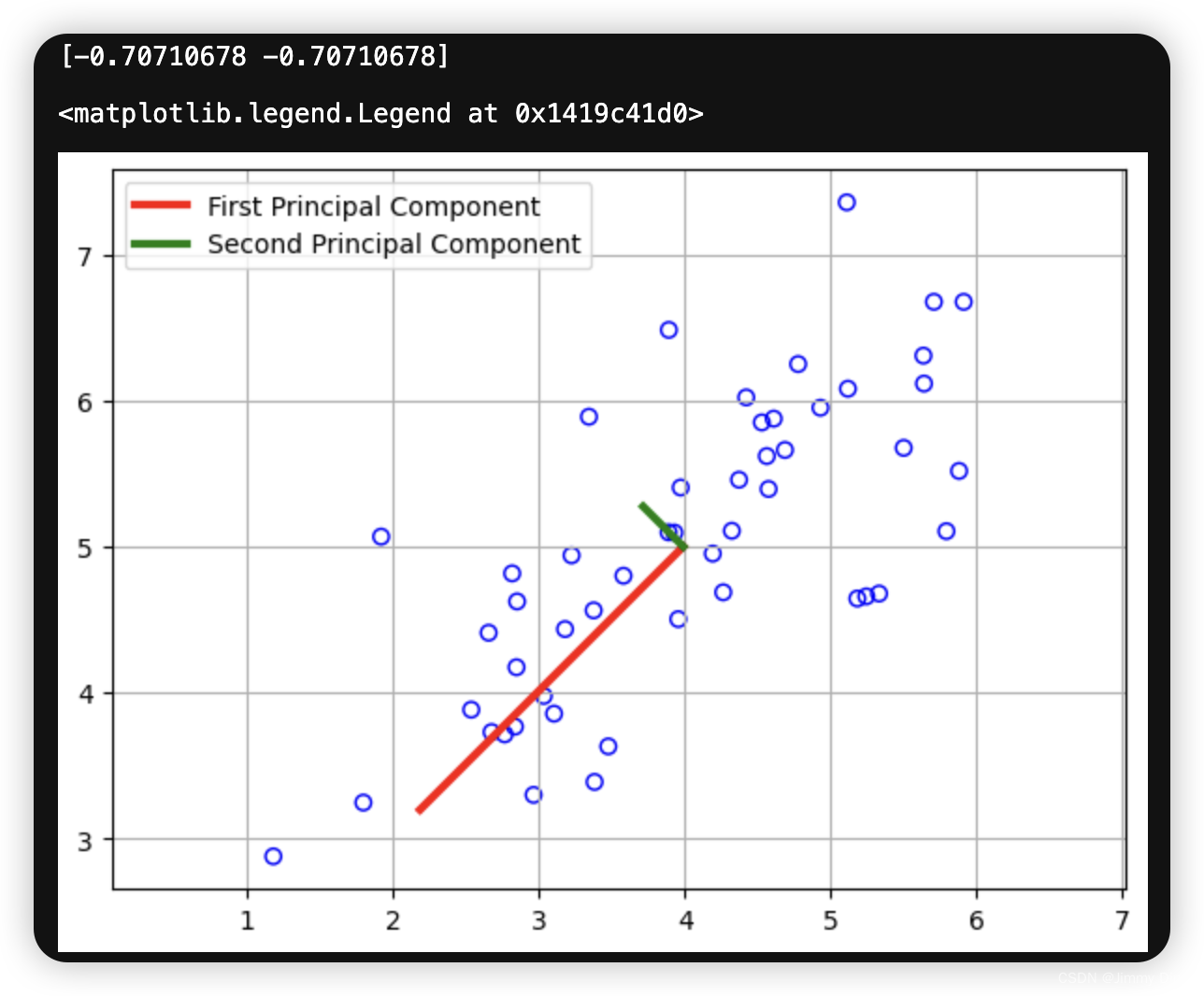
在这里插入图片描述

2.3 利用 PCA 降低维度

计算主成分后，您可以将每个示例投影到更低维度的空间 x(i) → z(i)（例如，将数据从二维投影到一维），从而利用主成分降低数据集的特征维度。在这部分练习中，您将使用 PCA 返回的特征向量，将示例数据集投影到一维空间中。实际上，如果您使用的是线性回归或神经网络等学习算法，您现在可以使用投影数据来代替原始数据。通过使用投影数据，您可以更快地训练模型，因为输入的维数更少。

2.3.1 将数据投影到主成分上

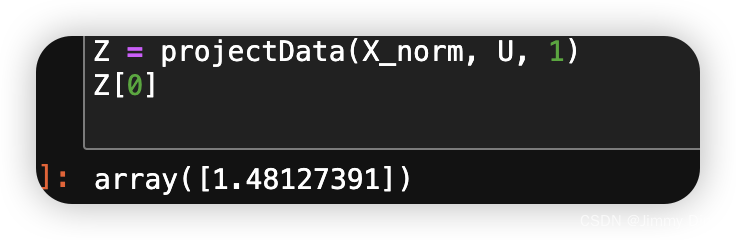
您现在应该完成 projectData.m 中的代码。具体来说，我们会给您一个数据集 X、主成分 U 和所需的维数 K，您应该将 X 中的每个示例投影到 U 中的前 K 个成分上。请注意，U 中的前 K 个分量由 U 的前 K 列给出，即 U reduce = U(:, 1:K)。完成 projectData.m 中的代码后，ex7 pca.m 会将第一个示例投影到第一个维度上，您应该会看到一个约为 1.481 的值（也可能是-1.481，如果您得到的是-U1 而不是 U1）。

def projectData(X, U, K):
    Z = X @ U[:, :K]
    return Z
'''
X @ U[:, :K] 表示将数据 X 投影到选择的主成分方向上。这里使用的是矩阵乘法。
这一步的结果是一个新的矩阵 Z，它的每一行表示一个样本在前 K 个主成分方向上的投影。
'''

在这里插入图片描述

2.3.2 重建数据近似值

在将数据投影到低维空间后，您可以通过将其投影回原始高维空间来近似恢复数据。您的任务是完成 recoverData.m，将 Z 中的每个示例投影回原始空间，并在 X rec 中返回恢复的近似值。
完成 recoverData.m 中的代码后，ex7 pca.m 将恢复第一个示例的近似值，您应该看到一个大约 [-1.047 -1.047] 的值。

def recoverData(Z, U, K):
    X_rec = Z @ U[:,:K].T
    
    return X_rec
X_rec = recoverData(Z, U, 1)
X_rec[0]
'''
Z: 降维后的数据矩阵，每行表示一个样本，每列表示一个主成分。
U: 主成分矩阵，包含所有主成分的方向向量。
K: 使用的主成分的数量。

U[:,:K]：从主成分矩阵 U 中选取前 K 个主成分方向向量。U 是一个形状为 (n, n) 的矩阵，
其中 n 是原始数据的特征数。U[:,:K] 是一个形状为 (n, K) 的矩阵。

Z @ U[:,:K].T：矩阵乘法。Z 是形状为 (m, K) 的降维数据矩阵，U[:,:K].T 是形状为 (K, n) 的矩阵，
它们的乘积 X_rec 是形状为 (m, n) 的矩阵，表示恢复的近似原始数据。
'''

在这里插入图片描述

2.3.3 预测的可视化

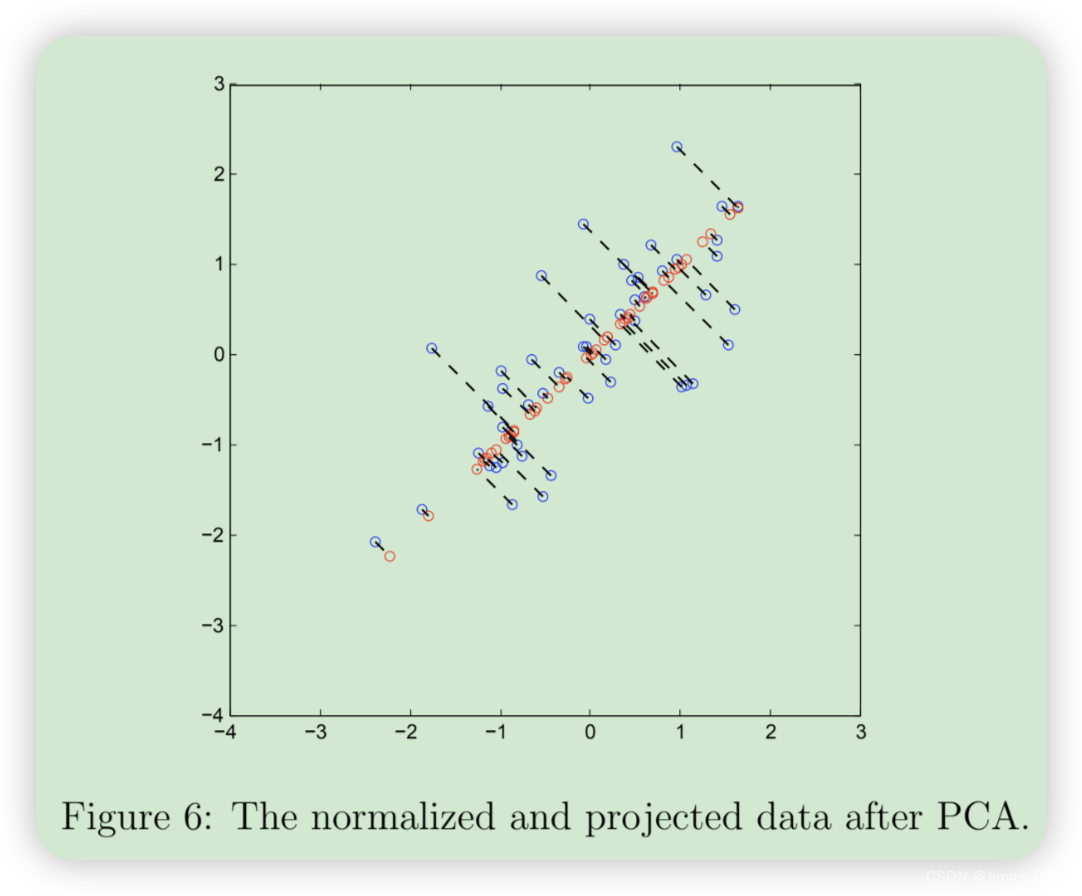
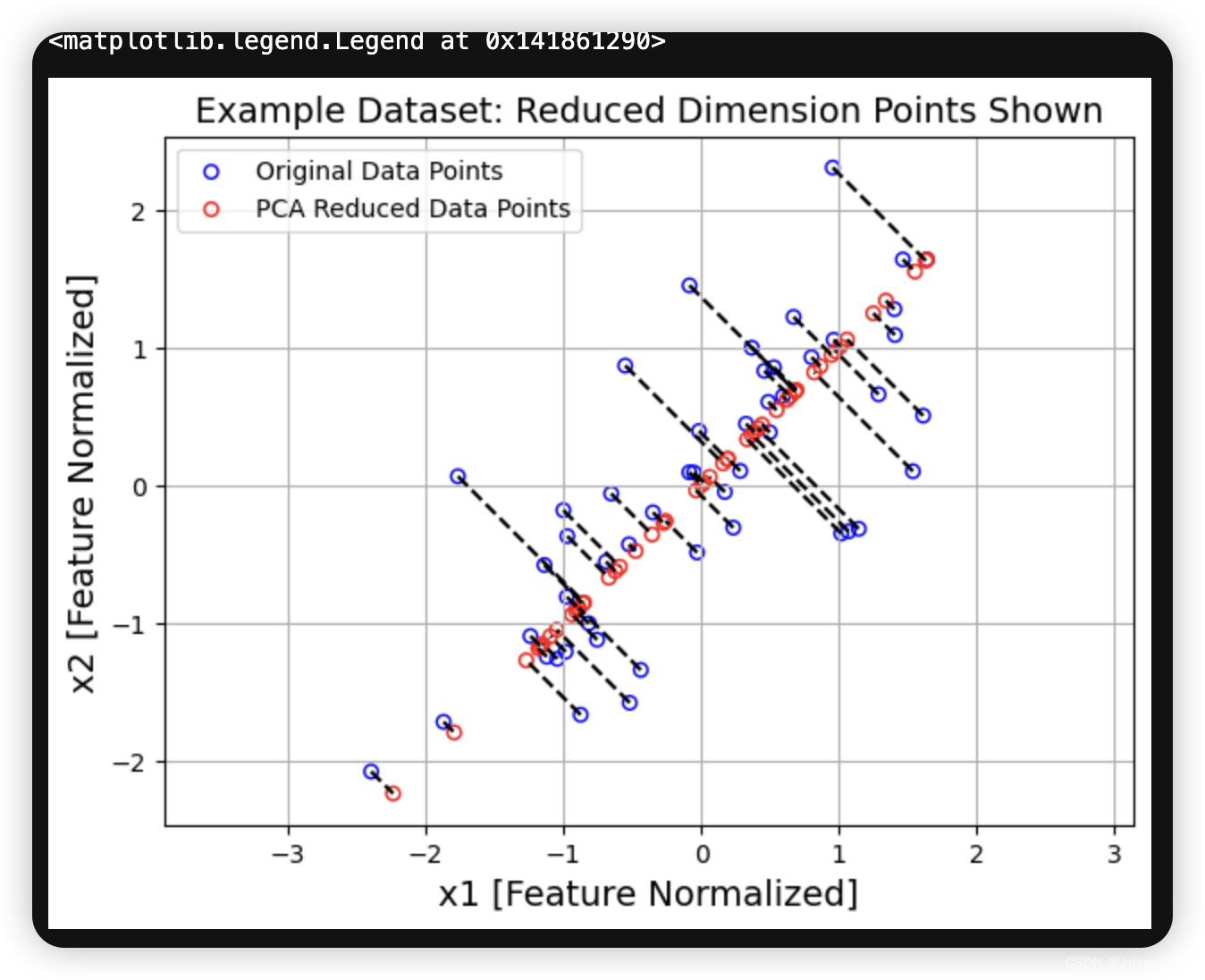
完成 projectData 和 recoverData 后，ex7 pca.m 将现在将同时执行投影和近似重建，以显示投影对数据的影响。图 6 中，蓝色圆圈表示原始数据点，红色圆圈表示投影后的数据点。投影实际上只保留了 U1 方向上的信息。
在这里插入图片描述

plt.figure(figsize=(7,5))  # 创建一个新的图形对象，并设置图形的尺寸（宽7英寸，高5英寸）
plt.axis("equal")  # 设置x轴和y轴的刻度比例相同，使得图形中的单位长度相同

plot = plt.scatter(X_norm[:,0], X_norm[:,1], s=30, facecolors='none', edgecolors='b', label='Original Data Points')
# 绘制原始数据点
# X_norm[:,0] 和 X_norm[:,1] 分别表示标准化后的数据的第一列和第二列
# s=30 表示散点的大小
# facecolors='none' 表示散点的内部颜色为空
# edgecolors='b' 表示散点的边缘颜色为蓝色
# label='Original Data Points' 为图例设置标签

plot = plt.scatter(X_rec[:,0], X_rec[:,1], s=30, facecolors='none', edgecolors='r', label='PCA Reduced Data Points')
# 绘制PCA降维后恢复的数据点
# X_rec[:,0] 和 X_rec[:,1] 分别表示恢复后的数据的第一列和第二列
# s=30 表示散点的大小
# facecolors='none' 表示散点的内部颜色为空
# edgecolors='r' 表示散点的边缘颜色为红色
# label='PCA Reduced Data Points' 为图例设置标签

plt.title("Example Dataset: Reduced Dimension Points Shown", fontsize=14)
# 设置图形的标题，并指定字体大小为14

plt.xlabel('x1 [Feature Normalized]', fontsize=14)
# 设置x轴的标签，并指定字体大小为14

plt.ylabel('x2 [Feature Normalized]', fontsize=14)
# 设置y轴的标签，并指定字体大小为14

plt.grid(True)  # 显示网格线

for x in range(X_norm.shape[0]):  # 遍历所有数据点
    plt.plot([X_norm[x,0], X_rec[x,0]], [X_norm[x,1], X_rec[x,1]], 'k--')
    # 绘制原始数据点和恢复数据点之间的连接线
    # X_norm[x,0] 和 X_rec[x,0] 分别是第x个数据点在原始数据和恢复数据中的x坐标
    # X_norm[x,1] 和 X_rec[x,1] 分别是y坐标
    # 'k--' 指定线条为黑色虚线

plt.legend()  # 显示图例，图例的内容由之前的label参数指定

在这里插入图片描述

2.4 人脸图像数据集

在这部分练习中，您将在人脸图像上运行 PCA，以了解如何在实践中将其用于降维。数据集 ex7faces.mat 包含一个由人脸图像组成的数据集3，每个图像都是 32 × 32 的灰度图像。X 的每一行对应一幅人脸图像（行向量长度为 1024）。ex7 pca.m 的下一步将加载前 100 张人脸图像并将其可视化（图 7）。
在这里插入图片描述


# Load data
mat = loadmat('data/ex7faces.mat')  # 从指定路径加载 MATLAB 文件
X = mat['X']  # 提取包含图像数据的矩阵 'X'
print(X.shape)  # 打印矩阵 'X' 的形状

def displayData(X, row, col):
    """
    显示图像数据的函数，将数据 X 显示为 row 行 col 列的图像网格
    参数:
    - X: 包含图像数据的矩阵，每一行表示一张图像
    - row: 图像网格的行数
    - col: 图像网格的列数
    """
    fig, axs = plt.subplots(row, col, figsize=(8,8))  # 创建一个包含 row 行 col 列的子图网格，并设置图像大小为 8x8 英寸
    fig.subplots_adjust(hspace=0.5, wspace=0.5)  # 调整子图之间的水平和垂直间距为 0.5
    num_images = row * col  # 总共显示的图像数量
    for r in range(row):  # 遍历每一行
        for c in range(col):  # 遍历每一列
            idx = r * col + c  # 计算当前图像在 X 中的索引
            if idx < len(X):  # 检查索引是否在范围内，以防止索引超出范围的错误
                axs[r][c].imshow(X[idx].reshape(32, 32).T, cmap='Greys_r')  # 显示图像，将一维数据重塑为 32x32 的图像，并进行转置以确保正确显示方向
            else:
                axs[r][c].axis('off')  # 如果没有更多图像，隐藏对应的子图
            axs[r][c].set_xticks([])  # 移除 x 轴刻度线
            axs[r][c].set_yticks([])  # 移除 y 轴刻度线

# 调用 displayData 函数，显示 10 行 10 列的图像网格
displayData(X, 10, 10)

在这里插入图片描述

2.4.1 面部 PCA

要在人脸数据集上运行 PCA，我们首先要对数据集进行归一化处理，即从数据矩阵 X 中减去每个特征的平均值。
每个特征的平均值。脚本 ex7 pca.m 将为您完成这项工作，然后运行 PCA 代码。运行 PCA 后，您将获得数据集的主成分。请注意，U（每一行）中的每个主成分都是长度为 n 的向量（对于人脸数据集，n = 1024）。事实证明，我们可以通过将每个主成分重塑为与原始数据集中的像素相对应的 32 × 32 矩阵来直观地显示这些主成分。脚本 ex7 pca.m 会显示描述最大变化的前 36 个主成分（图 8）。如果您愿意，也可以修改代码来显示更多的主成分，以了解它们是如何捕捉到越来越多的细节的。
在这里插入图片描述

# 对 X 进行归一化处理
X_norm, means, stds = featureNormalize(X)

# 对归一化后的 X 进行 PCA 分解
U, S, V = pca(X_norm)

# 打印 U 和 S 的形状
U.shape, S.shape

# 显示前 36 个主成分
displayData(U[:,:36].T, 6, 6)

在这里插入图片描述

2.4.2 降维

现在你已经计算出了人脸数据集的主成分，可以用它来降低人脸数据集的维度。这样，您就可以用较小的输入大小（例如 100 维）而不是原来的 1024 维来使用您的学习算法。ex7 pca.m 中的下一部分将把人脸数据集仅投影到前 100 个主成分上。具体来说，现在每个人脸图像都由一个向量 z(i) ∈ R100 来描述。要了解降维过程中损失了什么，可以只使用投影数据集来恢复数据。在 ex7 pca.m 中，会对数据进行近似恢复，原始和投影的人脸图像会并排显示（图 9）。从重建结果可以看出，人脸的总体结构和外观得到了保留，而细部细节却丢失了。例如，如果您要训练一个神经网络来进行人脸识别（获得人脸图像，预测人的身份），您可以使用维度减少的 100 维输入，而不是原始像素。
在这里插入图片描述

# 将数据投影到前 36 个主成分上
z = projectData(X_norm, U, K=36)

# 从降维后的数据恢复到原始空间
X_rec = recoverData(z, U, K=36)

# 显示恢复后的数据
displayData(X_rec, 10, 10)

在这里插入图片描述