系列文章目录
`
`
文章目录
- 系列文章目录
- 前言
- 1. 堆排序的基础知识
- 2. 堆排序详解
- 2.1 堆排序整体思路
- 2.2 思路详解
- 2.2.1 建堆
- 2.2.2 堆排序完整代码
- 2.2.3 输出数据
- 3. 时间复杂度分析
前言
1. 堆排序的基础知识
堆排序(Heap Sort)就是对直接选择排序的一种改进。此话怎讲呢?直接选择排序在待排序的n个数中进行n-1次比较选出最大或者最小的,但是在选出最大或者最小的数后,并没有对原来的序列进行改变,这使得下一次选数时还需要对全部数据进行比较,效率大大降低。
堆排序算法是Floyd和Williams在1964年共同发明的,同时他们发明了“堆”这种数据结构。
2. 堆排序详解
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0q6qLBDQ-1720192659452)(https://i-blog.csdnimg.cn/direct/0f2c72ccbaf94cb6b82fcf98db94d75b.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pho8P4Lh-1720192659453)(https://i-blog.csdnimg.cn/direct/276d4ccb5e3648eeb46bdd8931a2563e.png)]
2.1 堆排序整体思路
1):给出待排序的数组,咱们脑补一个逻辑结构,然后将该逻辑结构整体调整为大堆或者小堆。(建堆)
2): 留个问题:降序是构建大堆还是小堆呢?
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wF53FEr1-1720192659453)(https://i-blog.csdnimg.cn/direct/fe41635d2ec449d5a704a324e1a82319.png)]
3):打印输出数据。
2.2 思路详解
2.2.1 建堆
以大堆为例哈:既然前面都铺垫了向下调整算法,你们肯定猜到了是通过该算法来建堆啦。
注意该算法的使用前提:要求左右子树都是大堆。怎么办呢?聪明如你们,我们从逻辑结构的后面往前面用该算法不就行啦!!
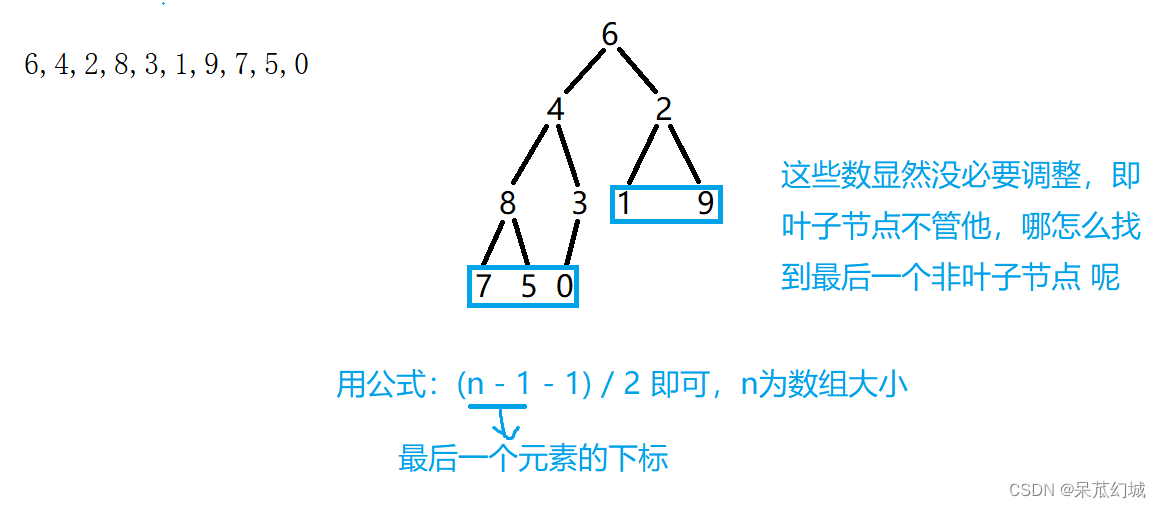
2.2.2 堆排序完整代码
#include <stdio.h>
//实现交换
void Swap(int* pa, int* pb)
{
int tmp = *pa;
*pa = *pb;
*pb = tmp;
}
//向下调整法
void AdjustDown(int* arr, int n, int root)
{
//双亲的下标
int parent = root;
//较大孩子的下标,默认为左孩子
int child = parent * 2 + 1;
//如果孩子的下标不越界,进入循环
while (child < n)
{
//如果右孩子存在(下标没越界),并且右孩子大于左孩子,更新child
if (child + 1 < n && arr[child + 1] > arr[child])
{
child = child + 1;
}
//如果较大的孩子大于双亲,交换
if (arr[child] > arr[parent])
{
Swap(&arr[child], &arr[parent]);
//改变parent的下标如果满足条件继续向下调整
parent = child;
child = parent * 2 + 1;
}
//如果较大的孩子不大于双亲,root节点的大堆构建完毕
else
{
break;
}
}
}
void HeapSort(int* arr, int n)
{
//循环从后面往前面对需要的数组元素使用向下调整算法
int i = 0;
//向下调整次数 (n-1-1)/2
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
//向下调整
AdjustDown(arr, n, i);
}
}
int main()
{
//待排序的数组
int arr[] = { 6,4,2,8,3,1,9,7,5,0 };
//调用主体函数
HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
//打印数据
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
return 0;
}
2.2.3 输出数据
这部分比较简单,不多分析。
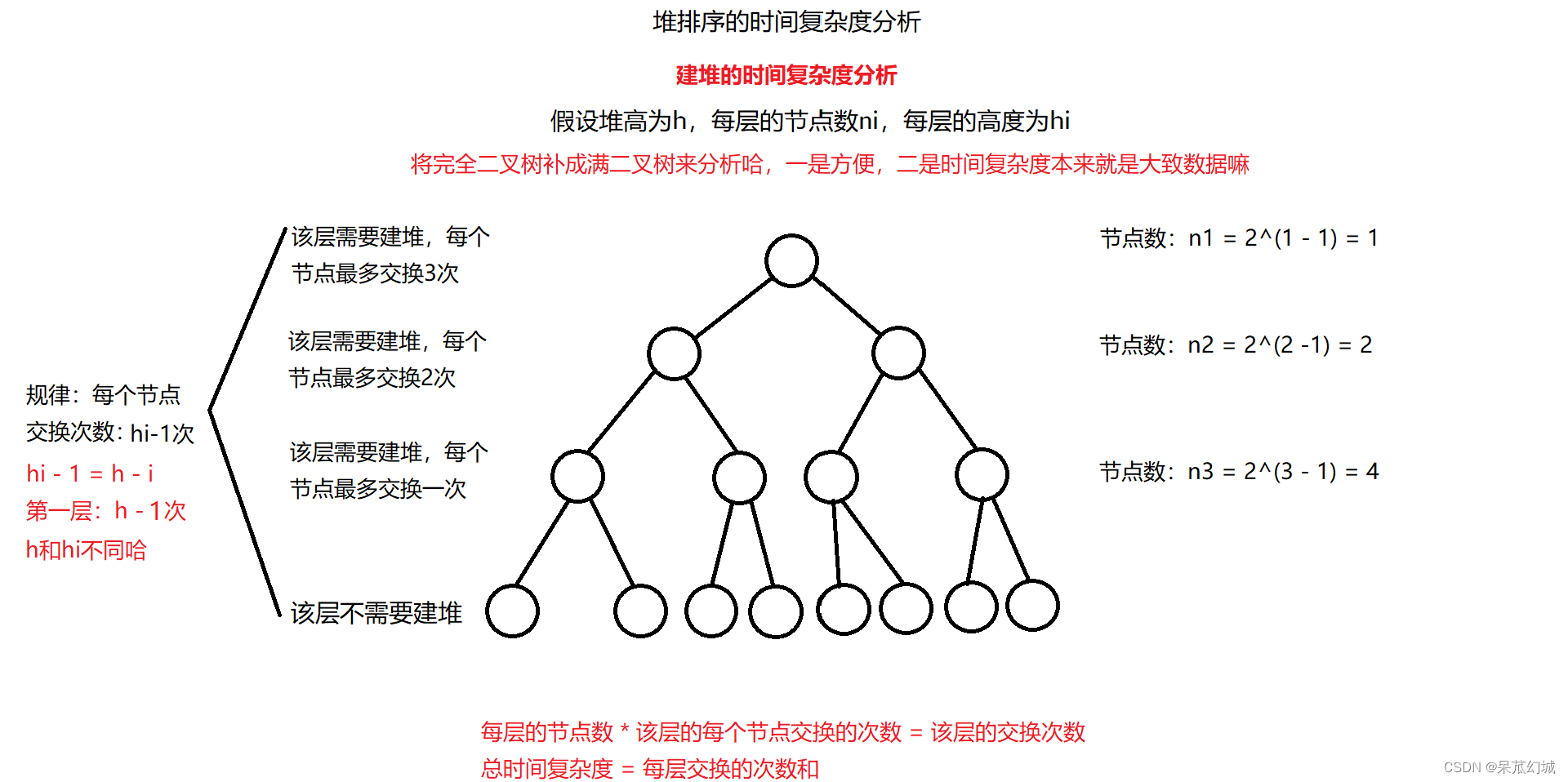
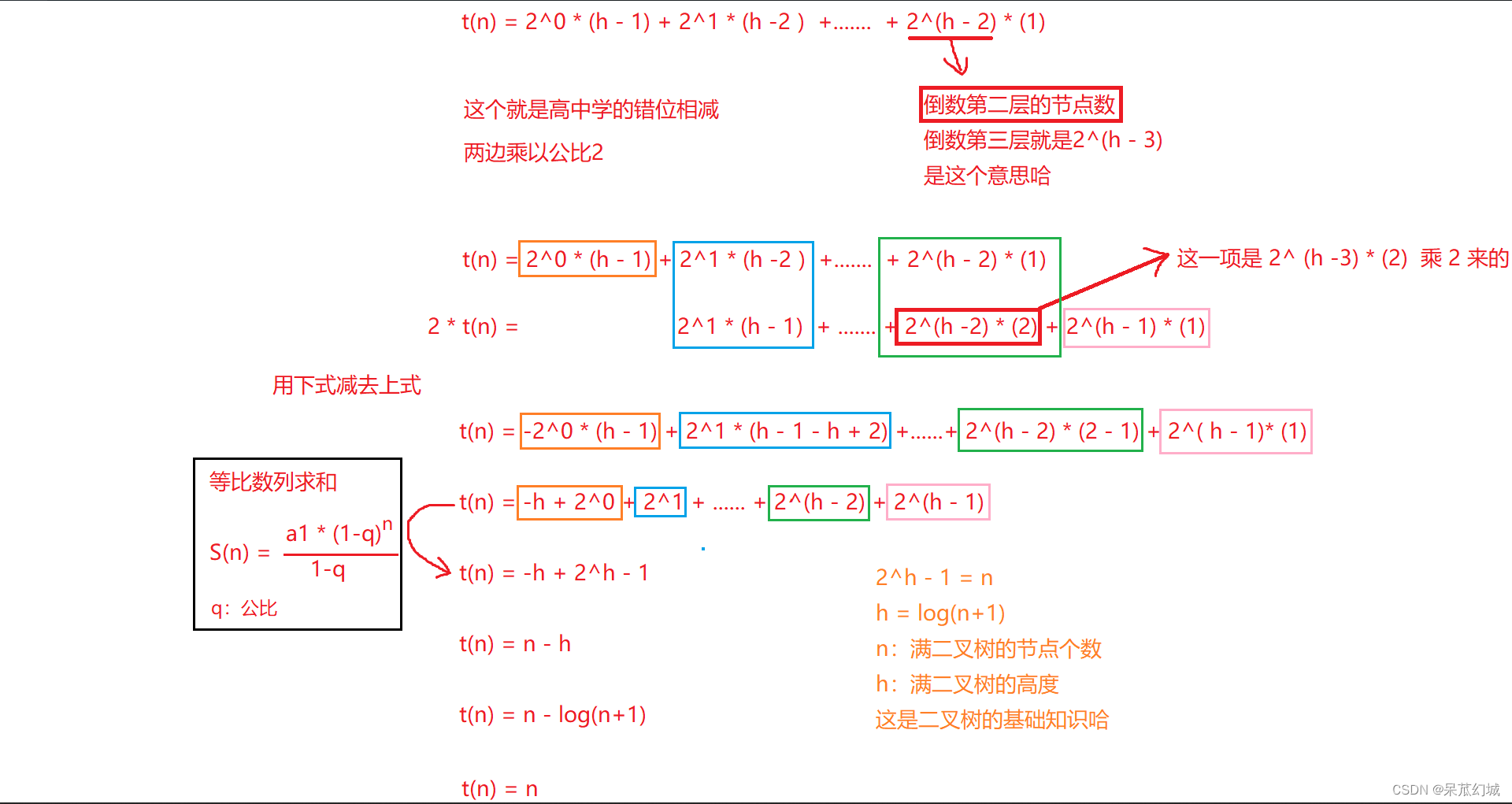
3. 时间复杂度分析
堆排序的时间复杂度分析,应该是排序算法中最复杂的,需要具备高中的基础知识!!!!