参考博客：

From Autoencoder to Beta-VAE | Lil'Log

链接：https://zhuanlan.zhihu.com/p/34998569

参考视频：

 https://www.youtube.com/watch?v=YNUek8ioAJk&ab_channel=Hung-yiLee

 

 

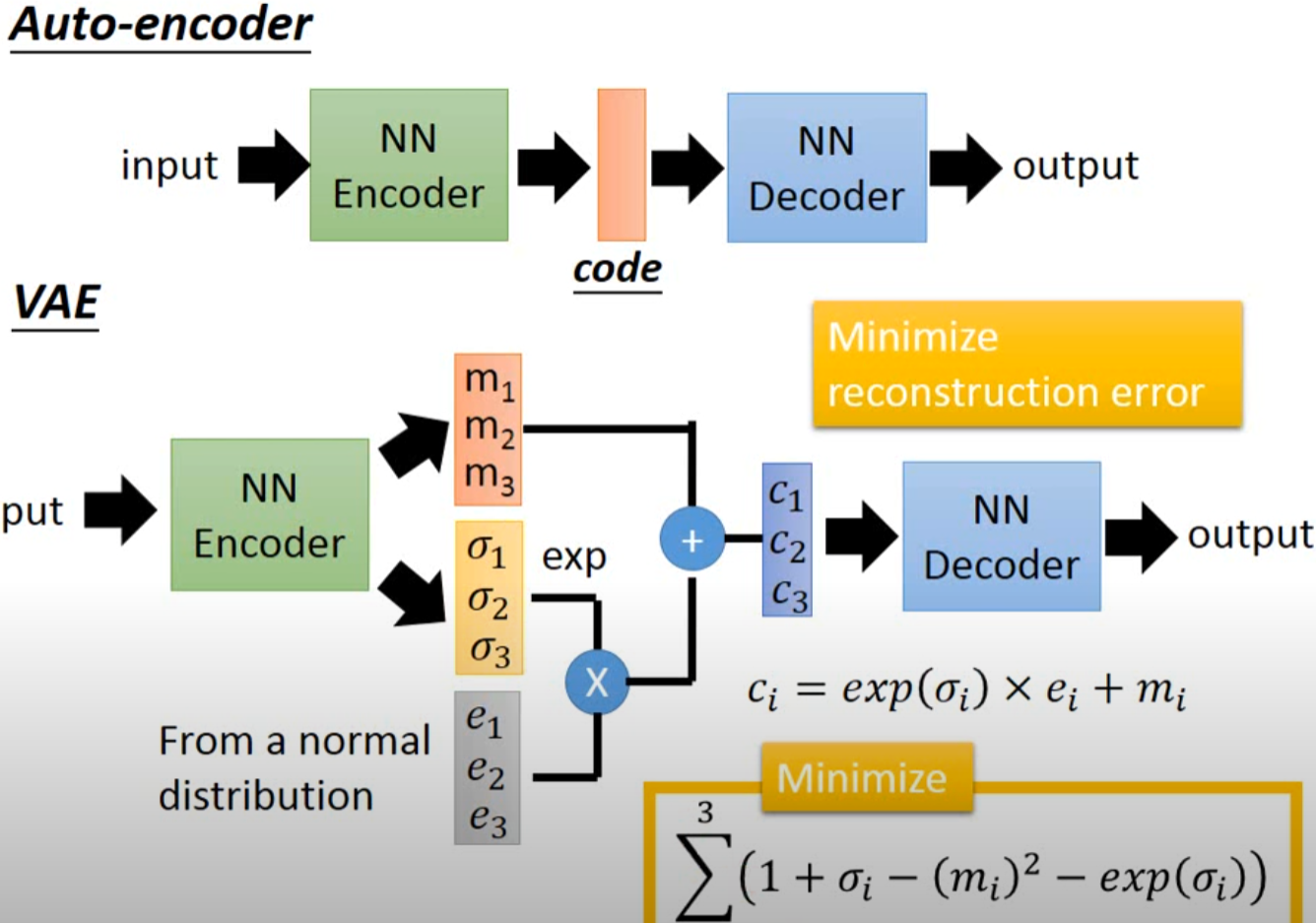
为了使模型具有生成能力，VAE 要求每个 p(Z_X) 都向正态分布看齐。

那怎么让所有的 p(Z|X) 都向 N(0,I) 看齐呢？如果没有外部知识的话，其实最直接的方法应该是在重构误差的基础上中加入额外的 loss：

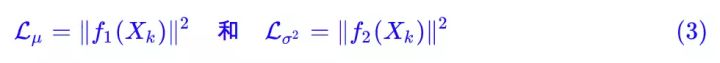
因为它们分别代表了均值 μk 和方差的对数 logσ^2，达到 N(0,I) 就是希望二者尽量接近于 0 了。不过，这又会面临着这两个损失的比例要怎么选取的问题，选取得不好，生成的图像会比较模糊。

所以，原论文直接算了一般（各分量独立的）正态分布与标准正态分布的 KL 散度KL(N(μ,σ^2)‖N(0,I))作为这个额外的 loss，计算结果为：

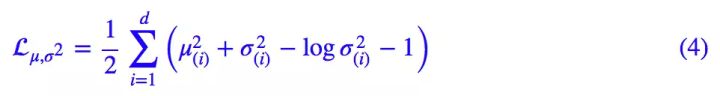
这里的 d 是隐变量 Z 的维度，而 μ(i) 和 σ_{(i)}^{2} 分别代表一般正态分布的均值向量和方差向量的第 i 个分量。直接用这个式子做补充 loss，就不用考虑均值损失和方差损失的相对比例问题了。