目录
剑指 Offer 34. 二叉树中和为某一值的路径
剑指 Offer 36. 二叉搜索树与双向链表
剑指 Offer 54. 二叉搜索树的第k大节点
剑指 Offer 34. 二叉树中和为某一值的路径
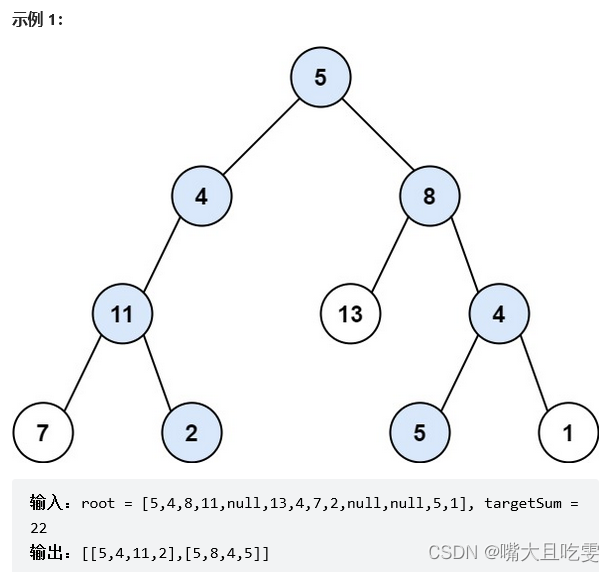
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/er-cha-shu-zhong-he-wei-mou-yi-zhi-de-lu-jing-lcof
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
【解法一】dfs
class Solution { public: vector<vector<int>> res; vector<int> temp; void dfs(TreeNode* root, int target) { if(root) { temp.push_back(root->val); target-=root->val; } if(root->left==nullptr && root->right==nullptr && target==0) { res.push_back(temp); temp.pop_back(); return; } if(root->left) { dfs(root->left, target); } if(root->right) { dfs(root->right, target); } temp.pop_back(); } vector<vector<int>> pathSum(TreeNode* root, int target) { if(root)dfs(root, target); return res; } };【解法二】上面的代码中间部分到达叶子结点加入一个return的原因是提前结束,提前结束了就不能走到下面pop的位置,所以需要把当前结点给pop出去
class Solution { public: vector<vector<int>> res; vector<int> temp; void dfs(TreeNode* root, int target) { if(root == nullptr)return; temp.push_back(root->val); target-=root->val; if(root->left==nullptr && root->right==nullptr && target==0) { res.push_back(temp); //temp.pop_back(); //return; } dfs(root->left, target); dfs(root->right, target); temp.pop_back(); } vector<vector<int>> pathSum(TreeNode* root, int target) { if(root)dfs(root, target); return res; } };
剑指 Offer 36. 二叉搜索树与双向链表
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
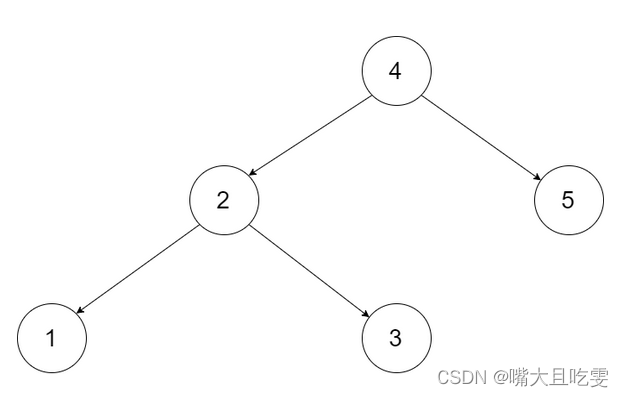
为了让您更好地理解问题,以下面的二叉搜索树为例:
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。【解法一】创建一个新的头结点,然后利用二叉搜索树的特点,进行中序遍历,按照中序遍历的每个元素值来创建新结点,然后依次将这些新结点尾插到头结点后面。
class Solution { public: Node* newhead = new Node(0); //创建新的头结点, Node* cur = newhead; //把后续中序遍历的结果依次尾插到新头结点后面 void preoder(Node* root) { if(root==nullptr)return; preoder(root->left); Node* newnode = new Node(root->val);//创建newnode cur->right = newnode; // 接入新的头结点中 cur = cur->right; // cur后移 处理下一个结点 preoder(root->right); } Node* treeToDoublyList(Node* root) { preoder(root); // 进行中序遍历 if(newhead->right) { Node* prev = newhead->right; cur = newhead->right->right; // 依次处理每个结点的left指向 while(cur) { cur->left = prev; prev = prev->right; cur = cur->right; } prev->right = newhead->right; newhead->right->left = prev; } return newhead->right; } };【解法二】使用一个数组来存储中序遍历的结果,然后依次遍历数组,处理每个结点的前后指针
class Solution { public: vector<Node*> res; void preoder(Node* root) { if(root==nullptr)return; preoder(root->left); res.push_back(root); // 中序遍历 将结点尾插入数组 preoder(root->right); } Node* treeToDoublyList(Node* root) { if(!root)return nullptr; preoder(root); for(int i = 0; i < res.size()-1; i++) { res[i]->right = res[i+1]; // 处理前后指向 res[i+1]->left = res[i]; } res[0]->left = res[res.size()-1]; res[res.size()-1]->right = res[0]; return res[0]; } };【方法三】原地修改,直接dfs递归遍历每个结点,创建俩个指针,prev与head,当中序遍历到最左侧第一个结点时,让head指向该结点,将当前结点指向prev,然后让prev移动到当前结点位置,返回上一结点,然后prev的right指向cur,cur的left也指向这个prev,然后继续一起往后走。
class Solution { public: Node *prev, *head; void dfs(Node* cur) { if(!cur)return; dfs(cur->left); if(prev)prev->right = cur; else head = cur; cur->left = prev; prev = cur; dfs(cur->right); } Node* treeToDoublyList(Node* root) { if(!root)return nullptr; dfs(root); prev->right = head; head->left = prev; return head; } };
剑指 Offer 54. 二叉搜索树的第k大节点
给定一棵二叉搜索树,请找出其中第
k大的节点的值。输入: root = [3,1,4,null,2], k = 1 3 / \ 1 4 \ 2 输出: 4【解法一】先序遍历放入数组中,返回size-k下标元素值
class Solution { public: vector<int> res; void Inoder(TreeNode* root) { if(!root)return; Inoder(root->left); res.push_back(root->val); Inoder(root->right); } int kthLargest(TreeNode* root, int k) { Inoder(root); return res[res.size()-k]; } };【解法二】
class Solution { public: int res = 0, k; void Inoder(TreeNode* root) { if(!root)return; Inoder(root->right); if(k==0)return; if(--k==0) { res = root->val; return; } Inoder(root->left); } int kthLargest(TreeNode* root, int k) { this->k = k; Inoder(root); return res; } };