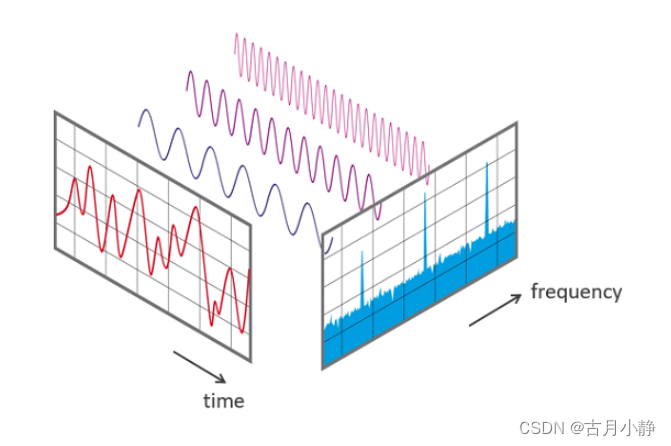
离散傅里叶变换(Discrete Fourier Transform,DFT)是信号分析中的一种基本方法,它将离散时序信号从时间域变换到频率域,是傅里叶变换在时域和频域都呈现离散的形式。以下是关于离散傅里叶变换的详细介绍:
一、定义与物理意义
定义:离散傅里叶变换是指将离散时间信号(即时间域上的离散序列)通过数学变换,转换为离散频率域上的表示形式。具体来说,设x(n)是长度为N的有限长序列,则其离散傅里叶变换X(k)可以表示为X(k) = ∑(n=0,N-1) x(n)e^(-i2πkn/N),其中k表示频率索引,N是序列的长度。
物理意义:离散傅里叶变换的物理意义在于,它将信号在时域上的采样转换为在离散时间傅里叶变换(DTFT)频域的采样。这种转换使得我们可以从频率的角度去分析信号的频谱结构和变化规律。
二、基本性质
离散傅里叶变换具有一系列重要的基本性质,包括线性性质、循环移位特性、隐含的周期性等。其中,线性性质表明DFT对线性组合的信号也满足线性关系;循环移位特性则表明DFT对信号的循环移位在频域上表现为相位的移动;隐含的周期性则指DFT在时域和频域上虽然表现为有限长的序列,但实质上可以看作是周期信号的主值序列。
三、应用
离散傅里叶变换在数字信号处理中有着广泛的应用,主要包括以下几个方面:
计算信号频谱:通过DFT可以计算出信号的频谱,即信号中各个频率分量的幅度和相位信息。这对于信号分析和处理至关重要。
系统分析:利用DFT可以分析系统的频率响应特性,从而了解系统对不同频率信号的响应情况。这对于系统设计和优化具有重要意义。
信号处理:DFT是某些精巧信号处理步骤中的中间步骤,如FFT卷积等。这些算法在信号处理领域具有广泛的应用价值。
四、计算与实现
在实际应用中,由于DFT的计算量较大,特别是对于较长序列的信号,直接计算DFT可能会非常耗时。因此,人们通常采用快速傅里叶变换(FFT)算法来高效计算DFT。FFT算法以DFT算法为基础,通过一系列的数学变换和优化手段,显著降低了计算复杂度,使得DFT在实际应用中更加高效和便捷。
五、注意事项
在使用离散傅里叶变换时,需要注意以下几个问题:
信号长度:DFT的长度N需要根据实际信号的特点和需求来确定。较长的N可以提供更高的频率分辨率,但同时也会增加计算量。
截断效应:在实际中遇到的信号往往是无限长的或者长度未知的,因此在使用DFT进行谱分析时,需要对信号进行截断处理。然而,截断处理可能会引入截断效应,导致分析结果出现误差。为了减少截断效应的影响,可以采用窗函数等方法对信号进行预处理。
频率分辨率:DFT的频率分辨率与信号长度N和采样频率fs有关。在给定采样频率下,增加N可以提高频率分辨率;但同时也会导致计算量增加。因此,在实际应用中需要根据具体需求来选择合适的N值。
总之,离散傅里叶变换是数字信号处理中的一种重要工具和方法,它为我们从频率角度分析和处理信号提供了有力支持。在实际应用中,我们需要根据具体需求选择合适的DFT长度和计算方法,并注意处理截断效应和频率分辨率等问题。