系统提示我未定义与 ‘double‘ 类型的输入参数相对应的函数 ‘finverse‘，如何解决？

news2024/11/20 13:42:29

🏆本文收录于「Bug调优」专栏，主要记录项目实战过程中的Bug之前因后果及提供真实有效的解决方案，希望能够助你一臂之力，帮你早日登顶实现财富自由🚀；同时，欢迎大家关注&&收藏&&订阅！持续更新中，up！up！up！！

问题描述

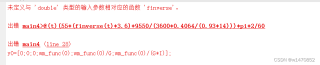
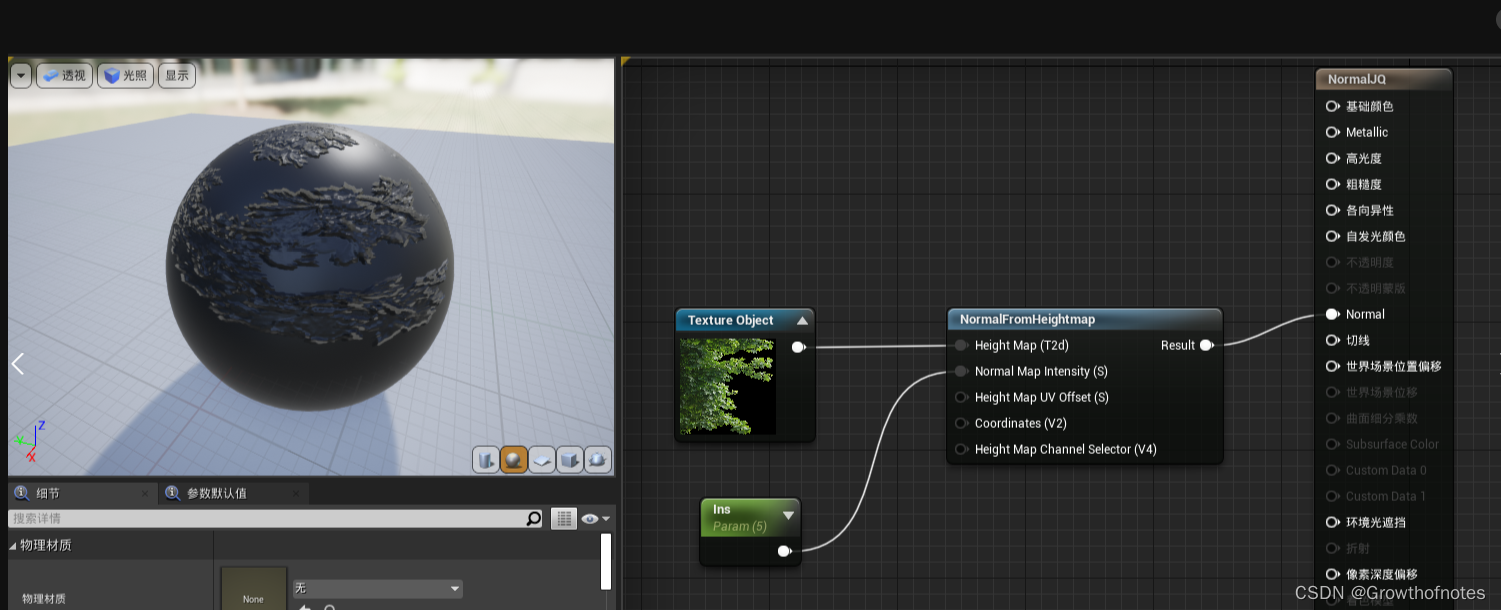
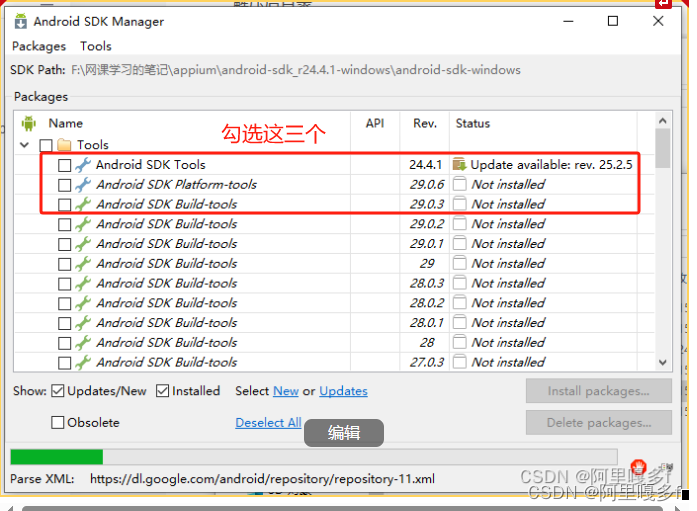
  核心是解三自由度微分方程组,解出θ关于时间t的变化图像.设定一个功率恒定变加速度的工况,图中时间t是关于速度v的函数,取反函数v=@(t)finverse(t)代入 wm_func中求得角速度.图一是主程序,图二是参数和方程.系统提示我未定义与 ‘double’ 类型的输入参数相对应的函数 ‘finverse’,如图三所示,想问一下我这个错在哪里有没有修改办法或者建议

clear;clc;close all;func
%初始参数，该参数变化，myfun程序要对应调整
syms t;
syms v;
t=@(v)(505.2*ln(49897/(55000-398.7*v))+1460*(12.8-v)/398.7);
v=@(t)finverse(t);     
wm_func = @(t)(55*(finverse(t)*3.6)*9550/(3600*0.4064/(0.93*14)))*pi*2/60;
 
zi=4;%内转子极对数
zo=14;%外转子极对数k
z1=32;%小齿轮齿数
z2=99;%大齿轮齿数
ms=4.62e-3;
I=z2/z1;%机械齿轮速比
G=(zo+zi)/zi;%磁齿轮速比
%一、计算过程
tmax=5;
tspan = 0:1e-4:tmax;
% tmax=900*2*pi/wm;% 计算时长，按输入轴的周期数计算
bc=2e-5;
y0=[0;0;0;wm_func(0);wm_func(0)/G;wm_func(0)/(G*I)];
% y0=[0;0;0;wm_func;wm_func/G;wm_func/(G*I)];
[t,y] = ode45(@(t,y)myfun3(t,y,wm_func), tspan, y0);
% [t,y] = ode45(@(t,y)myfun3(t,y), tspan, y0);
% [t,y]=odeRK4sys('myfun3',tmax,bc,y0);
 
figure;plot(t,y(:,1)/G-y(:,2));
title('时域响应图');
xlabel('时间 (s)');
ylabel('扭转振幅(rad)');%磁齿轮的相对弹性角度
figure;plot(t,y(:,2)/I-y(:,3));
title('时域响应图');
xlabel('时间 (s)');
ylabel('扭转振幅(rad)');%机械齿轮的相对弹性转角;
figure;plot(t,y(:,1),t,y(:,2),t,y(:,3));
title('时域响应图');
xlabel('时间 (s)');
ylabel('转速(rad/s)');
function dydt=myfun3(t,y,wm_func)
wm = wm_func(t);
zi=4;%内转子极对数
zo=14;%外转子极对数
z1=32;%小齿轮齿数
z2=99;%大齿轮齿数
arf0=20/180*pi;%压力角
ms=4.62e-3;
r2=ms*z1/2;%小齿轮分度圆
r3=ms*z2/2;%大齿轮分度圆
rb2=r2*cos(arf0);%小齿轮基圆
rb3=r3*cos(arf0);%大齿轮基圆
I=z2/z1;%机械齿轮速比
G=(zo+zi)/zi;%磁齿轮速比
% Tm =(1460*9.8*0.012+1.04*1460*2.67+0.32*2.25*(10+2.67*t*3.6)^2/21.15)*0.4064/(0.93*14);%起步加速
Tm=9550*55/(60*wm/(2*pi));                 ;
TL=Tm*I*G;%变速器负载
%3 转动惯量
IM=0.081197;%电机转子转动惯量kgm2
I0=0.181197;%磁齿轮低速级转动惯量kgm2
I1=0.013663;%磁齿轮高速级转动惯量kgm2
I2=0.0230596;%机械小齿轮转动惯量
I3=1.9825692;%机械大齿轮转动惯量
IL=21;%整车等效转动惯量
 
%4 刚度与阻尼
%齿轮的阻尼和刚度
w1=wm*G;%机械小齿轮输入转速
kp=10.51e8;
kb=0.25e8;%两个齿轮的刚度曲线为正弦曲线，
km=kp+kb*sin(w1*t*z1);
sg=0.16;%齿轮阻尼比
cm=2*sg*sqrt(kp*I2*I3/(I2*rb3^2+I3*rb2^2));
 b=2e-4;
 xx=rb2*y(2)-rb3*y(3);
 dxx=rb2*y(5)-rb3*y(6);
 
  if xx-b>0
      fx=xx-b;
  elseif xx+b<0
      fx=xx+b;
  else
      fx=0;
  end
F23=km*fx+cm*dxx;
T0=1.7*Tm*G;
Tc1=0.2*T0*sin(wm*t);
Tc=0.1*(zi*y(4)-(zi+zo)*y(5));
T21=T0*sin(zi*y(1)-(zi+zo)*y(2))+Tc+Tc1;
 
y(7)=(Tm-T21/G)/(I0+IM);
y(8)=(T21-r2*F23)/(I2+I1);
y(9)=(-TL+r3*F23)/(I3+IL);
 
dydt=[y(4)
      y(5)
      y(6)
      y(7)
      y(8)
      y(9)];
end

如上问题有来自我自身项目开发，有的收集网站，有的来自读者，如有侵权，立马删除。

解决方案

  如下是上述问题的解决方案，仅供参考：

  在 MATLAB 中，错误信息 “未定义与 ‘double’ 类型的输入参数相对应的函数 ‘finverse’” 通常表示 MATLAB 无法找到名为 finverse 的函数，该函数应该接受 ‘double’ 类型的输入参数。在您提供的代码中，问题出现在以下这行：

v=@(t)finverse(t);

这里，您尝试定义一个匿名函数 v，它使用 finverse 作为其操作。然而，finverse 并没有在您的代码中定义，或者没有被正确引用。

可能的解决方案：

  1. 定义 finverse 函数：如果 finverse 是您自定义的函数，确保它在 MATLAB 的搜索路径中，并且具有正确的定义。例如：
   function tinv = finv(t)
       % 这里是 finverse 函数的实现
       tinv = ... % 根据 t 计算逆函数的输出
   end
  1. 使用 MATLAB 内置函数：如果 finverse 应该是 MATLAB 的内置函数，确保函数名正确无误。例如，如果您想使用 fzero 函数来找到函数的零点，应该这样写：
   v = @(t) fzero(@(x) yourFunction(x) - t, initialGuess);

其中 yourFunction 是您要查找零点的函数，initialGuess 是一个初始猜测值。

  1. 检查变量作用域：如果您在其他地方定义了 finverse，请确保它可以在当前作用域中访问到。

  2. 检查拼写和大小写：MATLAB 是区分大小写的，确保函数名的拼写和大小写都是正确的。

  3. 使用 feval 或 eval：如果 finverse 是一个字符串形式的函数名，您可以使用 feval 或 eval 来调用：

   v = @(t) feval('finverse', t);

或者

   v = @(t) eval(['finverse(' num2str(t) ')']);

  1. 检查 MATLAB 版本：确保您使用的 MATLAB 版本支持您尝试调用的函数。

  2. 查看 MATLAB 函数索引：如果您不确定 finverse 的正确用法，可以查看 MATLAB 的函数索引或使用 helpwin finv（如果 finverse 是指 fmin 的逆函数，这可能是一个错误）。

特别注意：

  • 您提供的代码中 t 是关于 v 的函数，但您试图定义 v 为 t 的函数的反函数。这需要 t(v) 是一个单调函数，以便存在唯一的反函数。
  • 如果 t(v) 不是单调的，或者您没有正确定义 finverse，MATLAB 将无法计算 v(t)。

请根据上述建议检查和修改您的代码。如果 finverse 是您自定义的函数，请确保它在 MATLAB 的搜索路径中，并且具有正确的定义。如果 finverse 是内置函数或您打算使用特定的 MATLAB 函数，请确保正确引用它。

  希望如上措施及解决方案能够帮到有需要的你。

  PS：如若遇到采纳如下方案还是未解决的同学，希望不要抱怨&&急躁，毕竟影响因素众多，我写出来也是希望能够尽最大努力帮助到同类似问题的小伙伴，即把你未解决或者产生新Bug黏贴在评论区，我们大家一起来努力，一起帮你看看，可以不咯。

  若有对当前Bug有与如下提供的方法不一致，有个不情之请，希望你能把你的新思路或新方法分享到评论区，一起学习，目的就是帮助更多所需要的同学，正所谓「赠人玫瑰，手留余香」。

☀️写在最后

  ok，以上就是我这期的Bug修复内容啦，如果还想查找更多解决方案，你可以看看我专门收集Bug及提供解决方案的专栏「Bug调优」，都是实战中碰到的Bug，希望对你有所帮助。到此，咱们下期拜拜。

码字不易，如果这篇文章对你有所帮助，帮忙给bug菌来个一键三连(关注、点赞、收藏) ，您的支持就是我坚持写作分享知识点传播技术的最大动力。

同时也推荐大家关注我的硬核公众号:「猿圈奇妙屋」 ；以第一手学习bug菌的首发干货，不仅能学习更多技术硬货，还可白嫖最新BAT大厂面试真题、4000G Pdf技术书籍、万份简历/PPT模板、技术文章Markdown文档等海量资料，你想要的我都有！

📣关于我

我是bug菌，CSDN | 掘金 | InfoQ | 51CTO | 华为云 | 阿里云 | 腾讯云 等社区博客专家，C站博客之星Top30，华为云2023年度十佳博主，掘金多年度人气作者Top40，掘金等各大社区签约作者，51CTO年度博主Top12，掘金/InfoQ/51CTO等社区优质创作者；全网粉丝合计 30w+；硬核微信公众号「猿圈奇妙屋」，欢迎你的加入！免费白嫖最新BAT互联网公司面试真题、4000G PDF电子书籍、简历模板等海量资料，你想要的我都有，关键是你不来拿哇。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1896016.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【Linux】多线程（互斥 同步）

【Linux】多线程（互斥 同步）

我们在上一节多线程提到没有任何保护措施的抢票是会造成数据不一致的问题的。 那我们怎么办&#xff1f; 答案就是进行加锁。 目录 加锁&#xff1a;认识锁和接口&#xff1a;初始化&#xff1a;加锁 && 解锁&#xff1a;全局的方式&#xff1a;局部的方式&#xff1a…
阅读更多...
rtpengine_mr12.0 基础建设容器运行

rtpengine_mr12.0 基础建设容器运行

目录 Dockerfile rtpengine.conf 容器内编译安装 RTPEngine 正常提供功能 1. 启动RTPEngine服务 2. 删除 RTPEngine服务 3. 加载内核模块 检查所有进程是否正在运行 上传到仓库 博主wx&#xff1a;yuanlai45_csdn 博主qq&#xff1a;2777137742 后期会创建粉丝群&…
阅读更多...
地埋RF射频电子标识器探测仪ED8000（V400版）使用操作说明之1测量准备工作

地埋RF射频电子标识器探测仪ED8000（V400版）使用操作说明之1测量准备工作

地埋RF射频电子标识器探测仪ED8000&#xff08;V400版&#xff09;是一台集成了多频率、多种ID标识器调制模式、高低灵敏度调节、可读写标识器等全功能、高性能电子标识器探测仪。它有着极高的灵敏度,同时具备良好的噪声抑制能力&#xff0c;不仅适合专业测绘人员&#xff0c;普…
阅读更多...
监控平台—Zabbix对接grafana

监控平台—Zabbix对接grafana

目录 一、安装grafana并启动 二.浏览器访问 三、导入zabbix数据&#xff0c;对接grafana 四.如何导入模版 一、安装grafana并启动 添加一台服务器192.168.80.102 初始化操作 systemctl disable --now firewalld setenforce 0 vim /etc/selinux/config SELINUXdisabled cd /…
阅读更多...
东哥教你如何用Orange Ai pro为家里做一个垃圾分类检测机器

东哥教你如何用Orange Ai pro为家里做一个垃圾分类检测机器

前言 最近入手了一块香橙派&#xff08;Orange Ai Pro&#xff09;的板子&#xff0c;他们的口号是&#xff1a;为AI而生&#xff0c;这让一个算法工程师按捺不住了&#xff0c; 之前主要是在RKNN和ESP32等设备上部署AI模型&#xff0c;看到官方介绍的强大AI算力&#xff0c;很…
阅读更多...
入门PHP就来我这（纯干货）08

入门PHP就来我这（纯干货）08

~~~~ 有胆量你就来跟着路老师卷起来&#xff01; -- 纯干货&#xff0c;技术知识分享 ~~~~ 路老师给大家分享PHP语言的知识了&#xff0c;旨在想让大家入门PHP&#xff0c;并深入了解PHP语言。 1 PHP对象的高级应用 1.1 final关键字 final 最终的、最后的。被final修饰过的类…
阅读更多...
如何在电脑设备上恢复已删除的照片

如何在电脑设备上恢复已删除的照片

丢失 PC、智能手机或 USB 闪存盘上的照片可能会让人不知所措。幸运的是&#xff0c;使用最好的照片恢复软件&#xff0c;您可以在 Windows 和 Android 上恢复已删除的照片。本博客讨论如何使用照片恢复来恢复丢失的照片。 数码照片是我们记忆的重要组成部分。然而&#xff0c;它…
阅读更多...
UE4_材质基础_切线空间与法线贴图

UE4_材质基础_切线空间与法线贴图

学习笔记&#xff0c;不喜勿喷&#xff0c;侵权立删&#xff0c;祝愿大家生活越来越好&#xff01; 一、切线空间 在《OpenGL基础11&#xff1a;空间》中提到了观察空间、裁剪空间、世界空间等。切线空间和它们一样&#xff0c;都属于坐标空间 上面就是一个…
阅读更多...
FPGA的理解，个人的见解，不一定对

FPGA的理解，个人的见解，不一定对

类似于面包板上搭建电路&#xff0c;但是使用的是逻辑单元模块&#xff1b;如加法器&#xff0c;减法器&#xff0c;寄存器等 没有模拟电路的电容&#xff0c;电阻&#xff1b;但是逻辑单元的底层实现&#xff0c;使用MOS管等电路实现电路的开关&#xff1b;从而表示0&#xf…
阅读更多...
springai+pgvector+ollama实现rag

springai+pgvector+ollama实现rag

首先在ollama中安装mofanke/dmeta-embedding-zh:latest。执行ollama run mofanke/dmeta-embedding-zh 。实现将文本转化为向量数据 接着安装pgvector&#xff08;建议使用pgadmin4作为可视化工具&#xff0c;用navicate会出现表不显示的问题&#xff09; 安装好需要的软件后我们…
阅读更多...
【python】OpenCV—Nighttime Low Illumination Image Enhancement

【python】OpenCV—Nighttime Low Illumination Image Enhancement

文章目录 1 背景介绍2 代码实现3 原理分析4 效果展示5 附录np.ndindexnumpy.ravelnumpy.argsortcv2.detailEnhancecv2.edgePreservingFilter 1 背景介绍 学习参考来自&#xff1a;OpenCV基础&#xff08;24&#xff09;改善夜间图像的照明 源码&#xff1a; 链接&#xff1a…
阅读更多...
vue2 webpack使用optimization.splitChunks分包，实现按需引入，进行首屏加载优化

vue2 webpack使用optimization.splitChunks分包，实现按需引入，进行首屏加载优化

optimization.splitChunks的具体功能和配置信息可以去网上自行查阅。 这边简单讲一下他的使用场景、作用、如何使用&#xff1a; 1、没用使用splitChunks进行分包之前&#xff0c;所有模块都揉在一个文件里&#xff0c;那么当这个文件足够大、网速又一般的时候&#xff0c;首…
阅读更多...
原厂商是什么意思？云管平台原厂商有哪些企业？

原厂商是什么意思？云管平台原厂商有哪些企业？

最近不少IT小伙伴在问关于原厂商相关问题&#xff0c;今天我们就来简单回答一下&#xff0c;仅供参考&#xff01; 原厂商是什么意思&#xff1f; 原厂商&#xff0c;或称原厂&#xff0c;是指生产特定产品或零部件的原始厂家。 软件原厂商是什么意思&#xff1f; 软件原厂…
阅读更多...
课设：选课管理系统（Java+MySQL）

课设：选课管理系统（Java+MySQL）

在本博客中&#xff0c;我将介绍用Java、MySQL、JDBC和Swing GUI开发一个简单的选课管理系统。 技术栈 Java&#xff1a;用于编写应用程序逻辑MySQL&#xff1a;用于存储和管理数据JDBC&#xff1a;用于连接Java应用程序和MySQL数据库Swing GUI&#xff1a;用于构建桌面应用程…
阅读更多...
Let‘s Encrypt免费SSL证书申请最简单的步骤

Let‘s Encrypt免费SSL证书申请最简单的步骤

随着互联网的飞速发展&#xff0c;网络安全问题愈发凸显其重要性。而HTTPS协议作为保障网站数据传输安全的重要手段&#xff0c;已经得到了广泛的应用。 申请Lets Encrypt免费泛域名SSL证书步骤 登录来此加密网站&#xff0c;输入域名&#xff0c;可以勾选泛域名和包含根域。…
阅读更多...
Appium环境搭建，华为nova8鸿蒙系统（包括环境安装，环境配置）（一）

Appium环境搭建，华为nova8鸿蒙系统（包括环境安装，环境配置）（一）

1.安装代码工具包 appium python client pip install appium-python-client 2.安装JDK 参考链接： ant+jmeter+jenkins从0实现持续集成（Windows）-CSDN博客 3.下载并安卓SDK 下载地址：AndroidDevTools - Android开发工具 Android SDK下载 Android Studio下载 Gradle下载…
阅读更多...
搜维尔科技：详谈ART的工具追踪技术

搜维尔科技：详谈ART的工具追踪技术

您的生产流程中是否已经受益于刀具跟踪系统&#xff1f;您是否意识到它们的价值&#xff1f;因为它们可以优化您的装配顺序&#xff0c;从而节省您的时间和金钱。 目前我们提供两种工具跟踪解决方案&#xff1a; 1.ART与 VERPOSE的解决方案——易于使用的图像识别 安装在工…
阅读更多...
C语言 | Leetcode C语言题解之第213题打家劫舍II

C语言 | Leetcode C语言题解之第213题打家劫舍II

题目&#xff1a; 题解&#xff1a; int robRange(int* nums, int start, int end) {int first nums[start], second fmax(nums[start], nums[start 1]);for (int i start 2; i < end; i) {int temp second;second fmax(first nums[i], second);first temp;}retur…
阅读更多...
[激光原理与应用-97]：南京科耐激光-激光焊接-焊中检测-智能制程监测系统IPM介绍 - 1 - 什么是焊接以及传统的焊接方法

[激光原理与应用-97]：南京科耐激光-激光焊接-焊中检测-智能制程监测系统IPM介绍 - 1 - 什么是焊接以及传统的焊接方法

目录 一、什么是焊接 1.1 概述 1.2 基本原理 二、传统的焊接技术与方法 2.1 手工电弧焊&#xff1a; 1、定义与原理 2、特点 3、焊条类型 4、应用领域 5、安全注意事项 2.2 气体保护焊&#xff1a; 1、原理与特点 2、应用领域 3、气体选择 4、注意事项 2.3 电阻…
阅读更多...
六角法兰面螺栓机械性能

六角法兰面螺栓机械性能

六角法兰面螺栓&#xff0c;作为一种常见的紧固件&#xff0c;因其独特的设计和优良的机械性能&#xff0c;在众多工业领域中占据重要地位。与传统的六角头螺栓相比&#xff0c;六角法兰面螺栓的底部有一个扁平的法兰面&#xff0c;能够提供更大的接触面积&#xff0c;分散压力…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023