-
卡尔曼滤波器是一种有效的估计算法,主要用于在存在噪声的环境中估计动态系统的状态。它通过结合预测模型(系统动态)和观测数据(包括噪声)来实现这一点。在卡尔曼滤波中,调整过程噪声协方差矩阵 ( Q ) 和测量噪声协方差矩阵 ( R ) 是非常关键的,因为这两个参数直接影响滤波器的性能。
过程噪声 ( Q )
- 意义:( Q ) 表示对系统模型中随机噪声的估计。如果 ( Q ) 设置得较小,表明我们相信系统模型的精度较高,系统状态的预测与实际值差异不大。
- 调整策略:如果 ( Q ) 过小,滤波器对模型预测的信任度过高,可能会忽略一些实际中的动态变化,导致滤波结果跟不上实际系统的变化(系统易发散)。如果 ( Q ) 过大,滤波器对模型的信任度降低,会更多地依赖观测数据,这可能导致滤波输出过于嘈杂,反映了过多的测量噪声。
测量噪声 ( R )
- 意义:( R ) 表示对测量过程中噪声的估计。较大的 ( R ) 表示对测量数据的信任度较低。
- 调整策略:如果 ( R ) 过大,滤波器对测量数据的依赖减少,响应变慢,可能导致滤波器响应对系统变化不够敏感。如果 ( R ) 过小,滤波器对测量数据的信任度过高,这可能使滤波结果受到测量噪声的较大影响,导致估计值波动较大。
调试技巧
- 单变量调整:在调试过程中,通常建议固定一个噪声参数(如先固定 ( R )),调整另一个(如 ( Q )),观察滤波器的性能如何变化。这样可以分别了解每个参数的影响。
- 逐步调整:开始时可以将 ( Q ) 设置得较小,( R ) 设置得较大,然后逐步增加 ( Q )、减小 ( R ),观察滤波器的稳定性和响应速度。
- 性能指标:观察滤波器在调整参数后的性能,如估计误差、收敛速度、对系统变化的响应等。
实际应用中的考量
- 系统动态:系统的具体特性和动态变化也会影响最佳的 ( Q ) 和 ( R ) 值。例如,对于动态变化剧烈的系统,可能需要较大的 ( Q ) 来适应这种变化。
- 噪声特性:实际测量过程中噪声的统计特性(如方差、频谱)也应该在调整 ( R ) 时考虑。
总的来说,调整 ( Q ) 和 ( R ) 是一个迭代过程,需要基于系统性能反馈和实际观测数据来不断优化。在实际应用中,也可以利用一些自适应算法来动态调整这些参数,以达到更好的滤波效果。
https://yunyang1994.github.io/2021/07/10/%E5%8D%A1%E5%B0%94%E6%9B%BC%E6%BB%A4%E6%B3%A2%E7%AE%97%E6%B3%95-%E6%B0%B8%E8%BF%9C%E6%BB%B4%E7%A5%9E/
鲁道夫 • 卡尔曼在一次访问 NASA 埃姆斯研究中心时,发现他的卡尔曼滤波算法能帮助解决阿波罗计划的轨道预测问题,最终,飞船正确驶向月球,完成了人类历史上的第一次登月。卡尔曼因而一举成名,后来还被美国总统奥巴马授予了国家科学勋章。
S-G 滤波器(Savitzky–Golay filter),它的核心思想是对一定长度窗口内的数据点进行 k 阶多项式拟合,其加权系数是通过在滑动窗口内对给定高阶多项式的最小二乘拟合得出。
import numpy as np import matplotlib.pyplot as plt from scipy.signal import savgol_filter N = 100 # 数据点的数量 X = np.arange(N) # 创建一个0到N-1的数组 # 模拟100帧带有噪声的原始数据,使用正弦波和高斯噪声 Y1 = np.sin(np.linspace(0, np.pi*2, num=N)) + np.random.normal(0, 0.1, size=N) window_length = 5 # 滑动窗口长度,该值需为正奇整数 poly_order = 1 # 窗口内的数据点进行k阶多项式拟合,其值需要小于 window_length Y2 = [] # 用于存储平滑后的数据 cache_data = [] # 缓存队列,用于存储当前滑动窗口内的数据 for i in range(N): # 实时地遍历每帧噪声数据 origin_data = Y1[i] # 获取当前帧的数据 cache_data.append(origin_data) # 将当前帧数据添加到缓存队列 if i < window_length: # 如果当前帧数小于滑动窗口长度 smooth_data = origin_data # 直接使用原始数据作为平滑数据 else: window_data = np.array(cache_data) # 将缓存队列转换为numpy数组 window_data = savgol_filter(window_data, window_length, poly_order) # 对滑动窗口数据进行Savitzky-Golay滤波平滑 smooth_data = window_data[window_length//2] # 取滑动窗口中间位置的数据作为平滑结果 cache_data.pop(0) # 将缓存队列的最早数据移除,保持窗口大小不变 Y2.append(smooth_data) # 将平滑结果添加到结果列表中
观察这个过程,发现有个非常严重的 bug:被平滑的数据需要依赖前几帧,也就是说 S-G 滤波具有一定的滞后性,比如说如果 window_size = 5,那么就会滞后 2 帧。而卡尔曼滤波可以较好地解决这个问题的痛点,它只要获知上一时刻状态的估计值以及当前状态的观测值就可以计算出当前状态的估计值,因此不需要记录观测或者估计的历史信息


上述方程是卡尔曼滤波五个方程之一,名为状态更新 State Update Equation。其含义为:

因此,状态更新方程为:

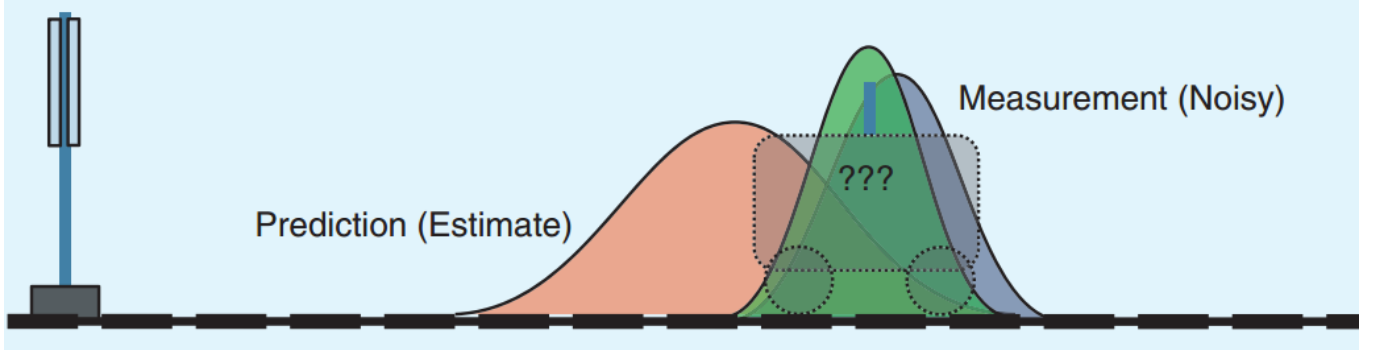
两种方法都有一定的可信度。那能否将两种答案相融合呢,卡尔曼滤波就是做了这样的事情。**如下图所示,假设两种方法的误差都满足正态分布,如下图所示。如果正态分布越尖锐陡峭,则说明这种方法的预测结果越可信;如果越缓和平坦,则说明越不可信。**为了融合这两种方法的预测结果,我们给这两种分布分别赋予一个权重,该权重代表了这个分布对融合结果的重要性。经过融合后的分布变得比之前两种分布更加尖锐,这表明结果更加可信了。

方差是权重,融合结果更接近方差小的
那么如何给出一个合理的权重分布呢,这就是卡尔曼滤波要做的事情。
卡尔曼滤波模型
Kalman 滤波分为 2 个步骤**,预测(predict)和校正(correct)。**
预测是基于上一时刻状态估计当前时刻状态,
校正则是综合当前时刻的估计状态与观测状态,估计出最优的状态。


**预测阶段负责根据前一时刻的状态估计值来推算当前时刻的状态变量先验估计值和误差协方差先验估计值;校正阶段负责将先验估计和新的测量变量相融合改进的后验估计。**卡尔曼滤波算法是一个递归的预测—校正方法,即只要获知上一时刻状态的估计值以及当前状态的观测值就可以计算出当前状态的估计值,因此不需要记录观测或者估计的历史信息。
从上面的五个公式中,我们发现:其实卡尔曼滤波的每次迭代更新就是为了求出卡尔曼增益 K,因为它代表了融合估计值和测量值之间的权重。下面这个视频很好地讲解如何通过最小化误差协方差矩阵求出 K:、
https://www.bilibili.com/video/BV1hC4y1b7K7/?t=565.857338&spm_id_from=333.1350.jump_directly&vd_source=8272bd48fee17396a4a1746c256ab0ae
Python 代码实现
在上面过程中,只有 PQRK 四个矩阵还尚未确定。显然增益矩阵 K 是不需要初始化的,P 是误差矩阵,初始化可以是一个随机的矩阵或者 0,只要经过几次的处理基本上就能调整到正常的水平,因此也就只会影响前面几次的滤波结果。
- Q:预测状态协方差,越小系统越容易收敛,我们对模型预测的值信任度越高;但是太小则容易发散,如果 Q 为零,那么我们只相信预测值;Q 值越大我们对于预测的信任度就越低,而对测量值的信任度就变高;如果 Q 值无穷大,那么我们只信任测量值;
- R:观测状态协方差,如果 R 太大,则表现它对新测量值的信任度降低而更愿意相信预测值,从而使得 kalman 的滤波结果会表现得比较规整和平滑,但是其响应速度会变慢而出现滞后;
- P:误差协方差初始值,表示我们对当前预测状态的信任度。它越小说明我们越相信当前预测状态;它的值决定了初始收敛速度,一般开始设一个较小的值以便于获取较快的收敛速度。随着卡尔曼滤波的迭代,P的值会不断的改变,当系统进入稳态之后P值会收敛成一个最小的估计方差矩阵,这个时候的卡尔曼增益也是最优的,所以这个值只是影响初始收敛速度。
假设系统的真实状态是一条正弦曲线,我们在测量过程中伴随一定正态分布的随机噪声,使用 python 模拟该过程如下:
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (10, 8) # 设置图形的显示大小
# 初始化参数
n_iter = 500 # 迭代次数
sz = (n_iter,) # 数组的大小
x = np.sin(np.linspace(0, np.pi*2, num=n_iter)) # 测量值,使用正弦函数生成
z = np.sin(np.linspace(0, np.pi*2, num=n_iter)) + np.random.normal(0, 0.1, size=n_iter) # 真实值,正弦值加上噪声
plt.figure() # 创建一个图形
plt.plot(z,'k+',label='noisy measurements') # 绘制噪声测量数据
plt.plot(x,color='g',label='truth value') # 绘制真实值
plt.legend() # 显示图例
plt.show() # 显示图形

接下来我们使用卡尔曼滤波对这段噪声进行实时去燥和平滑处理:
# 为数组分配空间
xhat=np.zeros(sz) # 后验估计值
P=np.zeros(sz) # 后验误差估计
xhatminus=np.zeros(sz) # 先验估计值
Pminus=np.zeros(sz) # 先验误差估计
K=np.zeros(sz) # 增益或融合因子
# 超参数设定,实测调整
R = 0.1**2 # 观测噪声的方差
Q = 1e-4 # 过程噪声的方差
# 初始猜测
xhat[0] = 0.0
P[0] = 1.0
for k in range(1, n_iter):
# 预测阶段
xhatminus[k] = xhat[k-1] # 根据前一个后验估计值预测当前值
Pminus[k] = P[k-1] + Q # 更新预测误差的协方差
# 更新阶段
K[k] = Pminus[k] / (Pminus[k] + R) # 计算卡尔曼增益
xhat[k] = xhatminus[k] + K[k] * (z[k] - xhatminus[k]) # 根据观测更新当前估计
P[k] = (1 - K[k]) * Pminus[k] # 更新误差协方差
plt.plot(z, 'k+', label='noisy measurements') # 绘制噪声测量值
plt.plot(x, color='g', label='truth value') # 绘制真实值
plt.plot(xhat, 'b-', label='a posteri estimate') # 绘制后验估计值
plt.legend() # 显示图例
plt.show() # 显示图形

贝叶斯定理(原理)
https://www.liaoxuefeng.com/article/1565255725482019

贝叶斯定理的核心思想就是不断根据新的证据,将先验概率调整为后验概率,使之更接近客观事实。
在贝叶斯公式中,各个部分的定义如下:
贝叶斯公式通常写作:
[
P
(
A
∣
B
)
=
P
(
B
∣
A
)
×
P
(
A
)
P
(
B
)
P(A|B) = \frac{P(B|A) \times P(A)}{P(B)}
P(A∣B)=P(B)P(B∣A)×P(A)
]
其中:
- ( P(A|B) ) 是 后验概率(Posterior Probability):在观察到事件 ( B ) 之后,事件 ( A ) 发生的概率。
- ( P(B|A) ) 是 似然概率(Likelihood):已知事件 ( A ) 发生时,观察到事件 ( B ) 的概率。
- ( P(A) ) 是 先验概率(Prior Probability):在观察到事件 ( B ) 之前,事件 ( A ) 发生的概率。
- ( P(B) ) 是 边际概率(Marginal Probability) 或 标准化常数(Normalizing Constant):事件 ( B ) 发生的总概率,无论事件 ( A ) 是否发生。
在贝叶斯理论中,后验概率 ( P ( A ∣ B ) P(A|B) P(A∣B) ) 是我们最关心的,因为它提供了考虑了新证据后事件 ( A A A ) 的更新概率。先验概率 ( P ( A ) P(A) P(A) ) 表示在获得新的数据或证据之前对事件 ( A A A ) 发生概率的假设或估计。