[导读]：超平老师的Scratch蓝桥杯真题解读系列在推出之后，受到了广大老师和家长的好评，非常感谢各位的认可和厚爱。作为回馈，超平老师计划推出《Python蓝桥杯真题解析100讲》，这是解读系列的第91讲。

最大奖品数，本题是2022年4月23日举办的第13届蓝桥杯青少组Python编程省赛真题编程部分第6题，13届一共举办了两次省赛，这是第二次省赛。题目要求对于给定的N * M矩阵方格数据，请编程计算最多可获得的奖品数。

先来看看题目的要求吧。

一.题目描述

时间限制：3000MS

内存限制：589824K8

编程实现：

有一个N * M的矩阵方格，其中有些方格中有奖品，有些方格中没有奖品。小蓝需要从N * M的矩阵中选择一个正方形区域，如果所选的正方形区域的一条对角线方格中都有奖品，其他方格都没有奖品，就会获得所选区域中的所有奖品，否则不能获得奖品。

当给出N和M的值，及N * M的矩阵方格中摆放的奖品情况

例如：N = 5，M = 6，奖品情况如下：

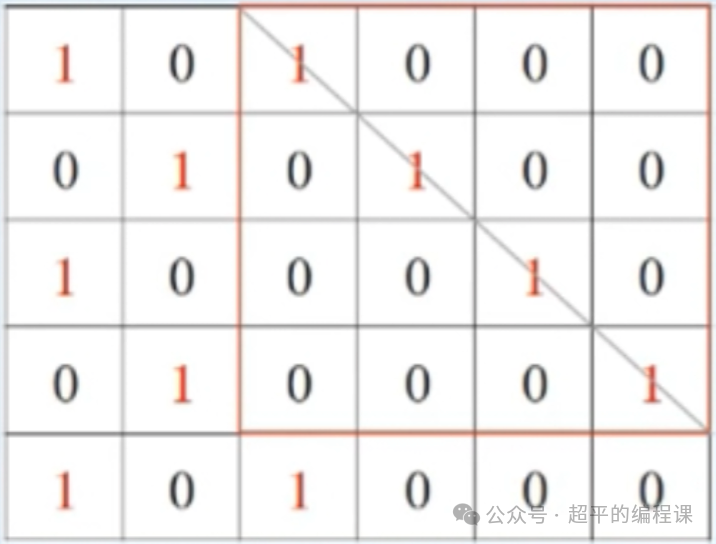
选择上图红色正方形区域，可以获得最多的4个奖品。

输入描述：

第一行输入两个整数N和M（1 ≤ N ≤ 100，1 ≤ M ≤ 100），N表示矩阵的行数，M表示矩阵的列数，两个整数之间一个空格隔开

接下来输入N行，每行包括M个0或者1（0表示方格中没有奖品，1表示方格中有奖品），0或者1之间一个空格隔开

输出描述：

输出一个整数，表示最多可获得的奖品数

输入样例：

5 6

1 0 1 0 0 0

0 1 0 1 0 0

1 0 0 0 1 0

0 1 0 0 0 1

1 0 1 0 0 0

输出样例:

4

评分标准：

• 20分：能正确输出一组数据；

• 20分：能正确输出两组数据；

• 20分：能正确输出三组数据；

• 20分：能正确输出四组数据；

• 20分：能正确输出五组数据。

二.思路分析

这是一道涉及二维矩阵遍历的算法题，涉及的知识点包括循环、条件、二维列表、自定义函数、枚举算法和DFS算法等。

题目有一定的难度，首先得搞清楚构成正方形区域有哪些情况，又有什么特点。

正方形只有一个，但是对角线有两条，一条是从右上到左下，一条是从左上到右下。为了方便描述，我们将前者称为撇，后者称为捺，就是笔画中的撇（丿）和捺（乀），还是挺形象的吧。

我们分别举例说，在一个5 x 6的矩阵方格中，撇构成的正方形如下：

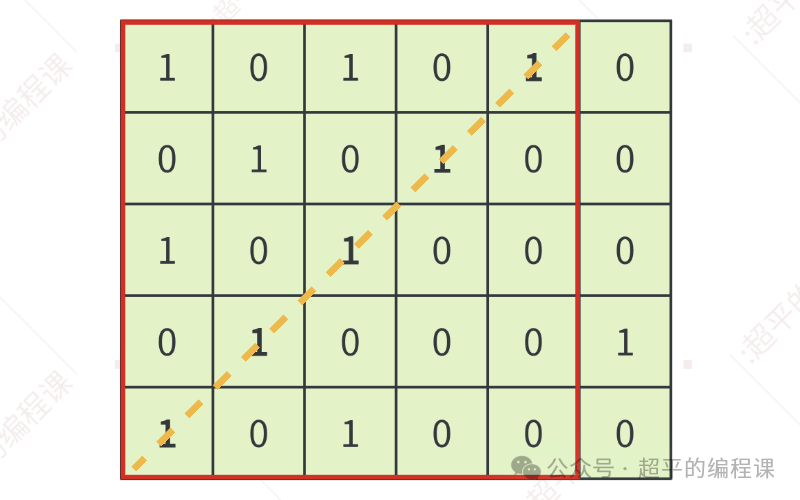
捺构成的正方形如下：

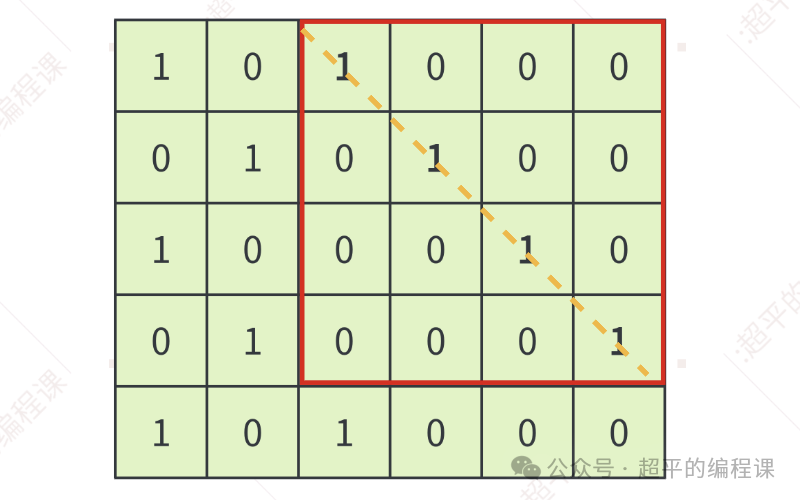
当然，正方形也可能是在中间某个区域，如图：

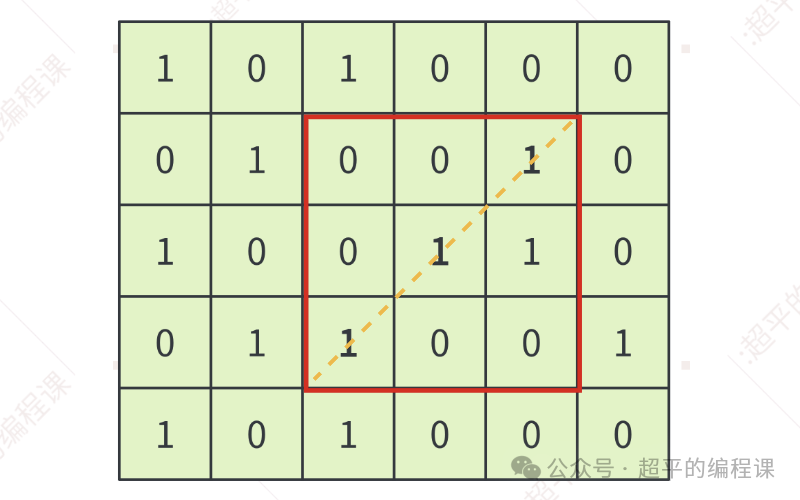
根据上面的分析，我们应该把焦点放在对角线上，同时还需要注意一点，只有对角线方格全为1，其它位置方格全为0的正方形才能获得奖品。

因此，在上面给出的3个例子中，第一个和第三个除了对角线上都是1外，正方形区域内还有其它的方格为1，所以不能获得奖品，第二个例子中可以获得4个奖品。

因此，对于任何一个值为1的单元格，我们都需要计算撇（丿）对角线和捺（乀）对角线的最大长度，同时确保其正方形区域内其它方格内没有1。

为了方便计算，我们可以将当前单元格作为起点，分别计算撇对角线和捺对角线的最大长度，同时确保其对应的正方形区域只有对角线上都为1。

比如，对于下图中的单元格[2][3]来说，将其作为起点，捺（乀）对角线（只考虑右下方，不考虑左上方）的最大长度是3，对应的是一个3 * 3的正方形，在正方形区域中只有3个方格为1，且都在对角线上，所以可以获奖，奖品数为3。

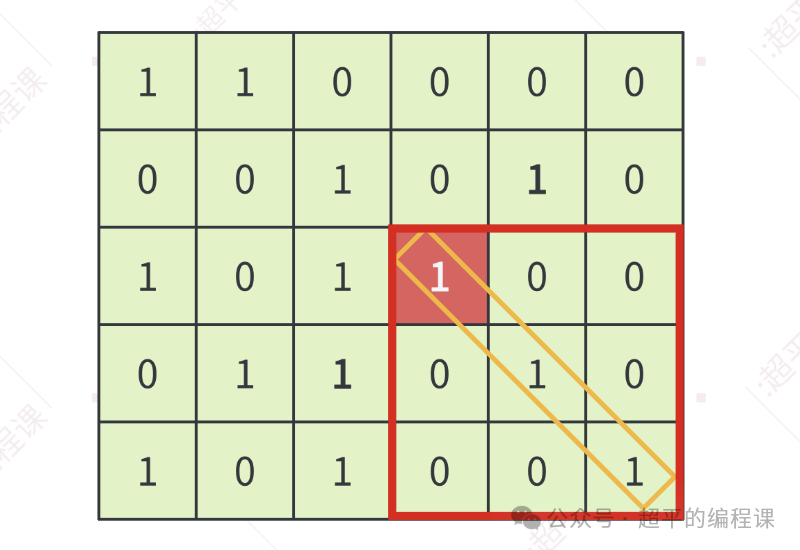
而撇（丿）对角线（只考虑左下方，不考虑右上方）的最大长度为2，对应的是一个2 * 2的正方形，但是正方形区域中有3个单元格为1，因此这条对角线不能获奖。

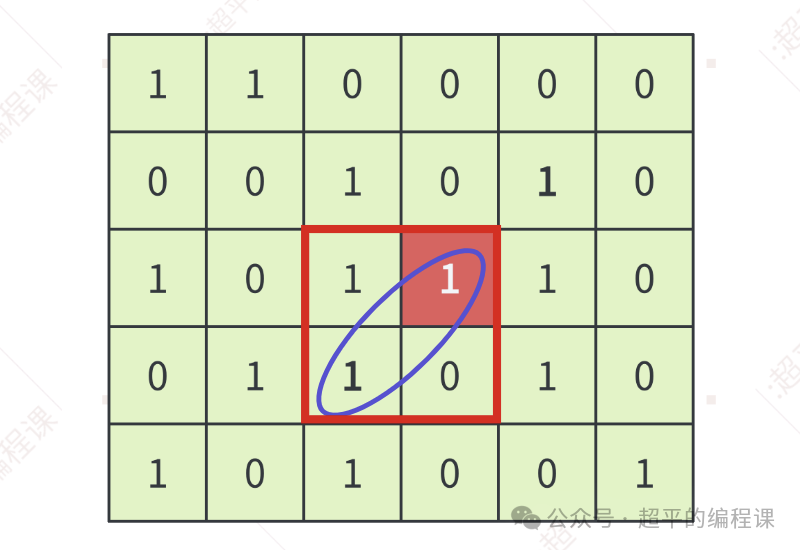
所以，对于撇对角线而言，其最大长度只能是1，如下：

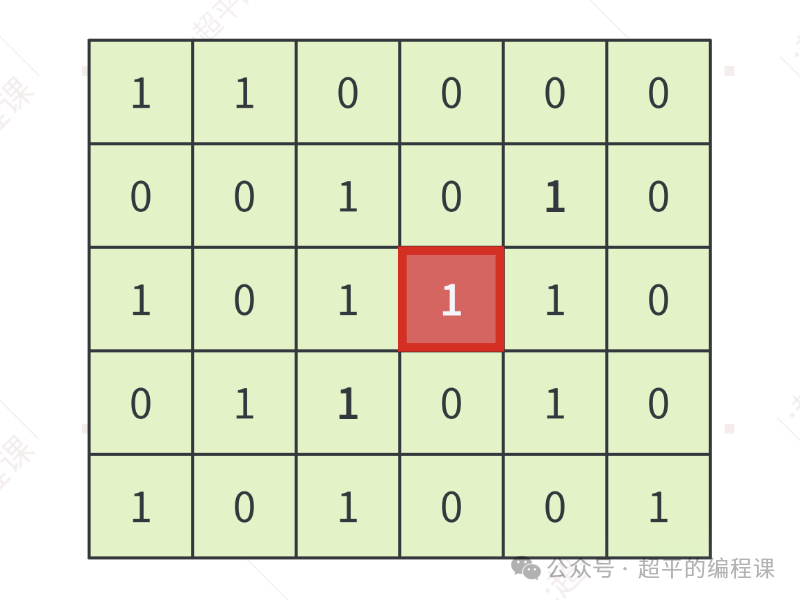
然后取两者中的较大值，因此单元格[2][3]最多可获得的奖品数为3。

看到这里，你是不是已经有点思路了？

沿着一个方向搜索，直到不满足条件为止，这不就是DFS算法吗。

DFS是指深度优先搜索，其核心思想是尽可能地搜索某一个分支，直到这个分支到达最深处时才返回。

还是以单元格grid[2][3]为例，在计算捺对角线上的时候，一直向右下方搜索，直到到达边缘或者单元格是0为止。

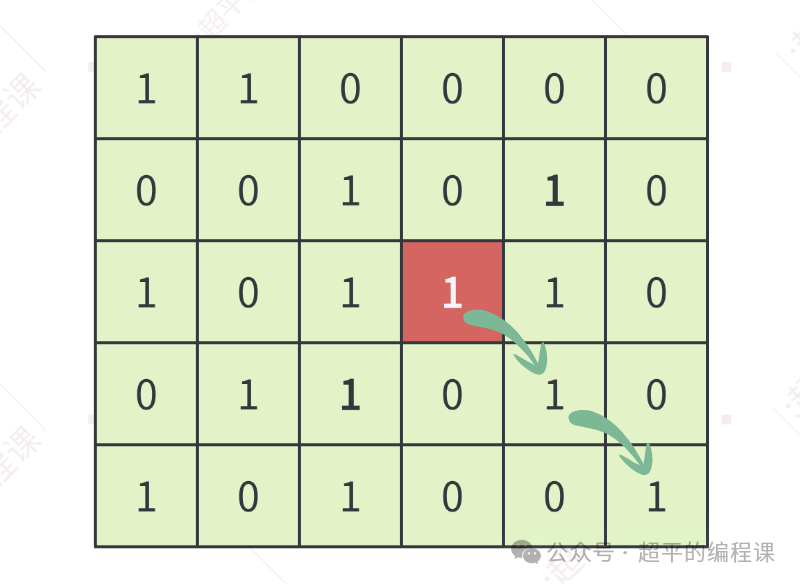
当然，还需要考虑一个条件，就是每向右下方走一格，都需要判断由该对角线构成的正方形区域中的1是否都在对角线上，如果满足就继续搜索，否则就返回。

再来看看撇的情况，如图：

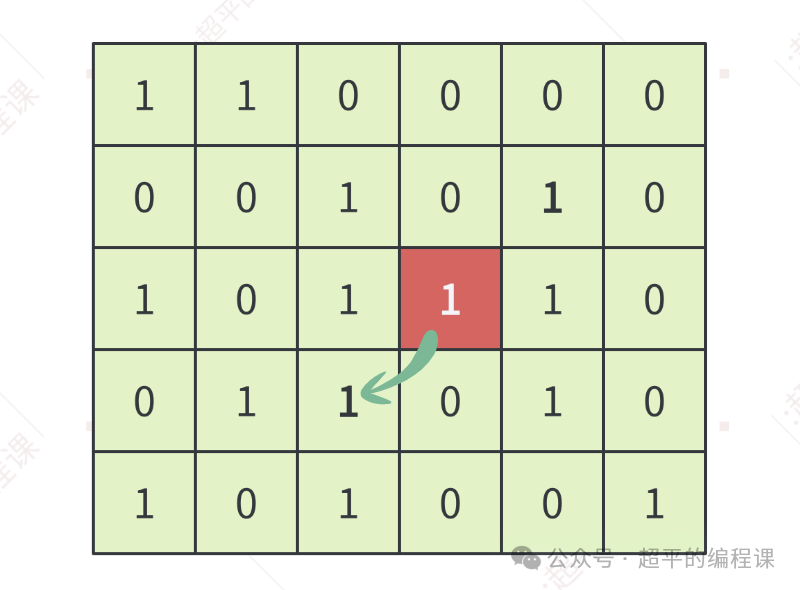
同理，只需要向左下方不断搜索即可，如果左下方的单元格不为1，停止搜索，如果到达边缘了，停止搜索，如果所构成的正方形中的1不都在对角线上，停止搜索。

为了方便，我们可以定义两个dfs函数，分别沿着两个方向进行搜索，计算其最大的奖品数量。

在dfs函数中，还需要计算对角线所构成的正方形区域中1的个数，也可以使用自定义函数来计算。

思路有了，接下来，我们就进入具体的编程实现环节。

三.编程实现

根据上面的思路分析，我们分两步来编写程序：

• 自定义函数

• 遍历矩阵计算最大值

1. 自定义函数

根据前面的思路分析，我们需要定义3个函数。

a. 计算并判断正方形区域中1的数量

自定义函数如下：

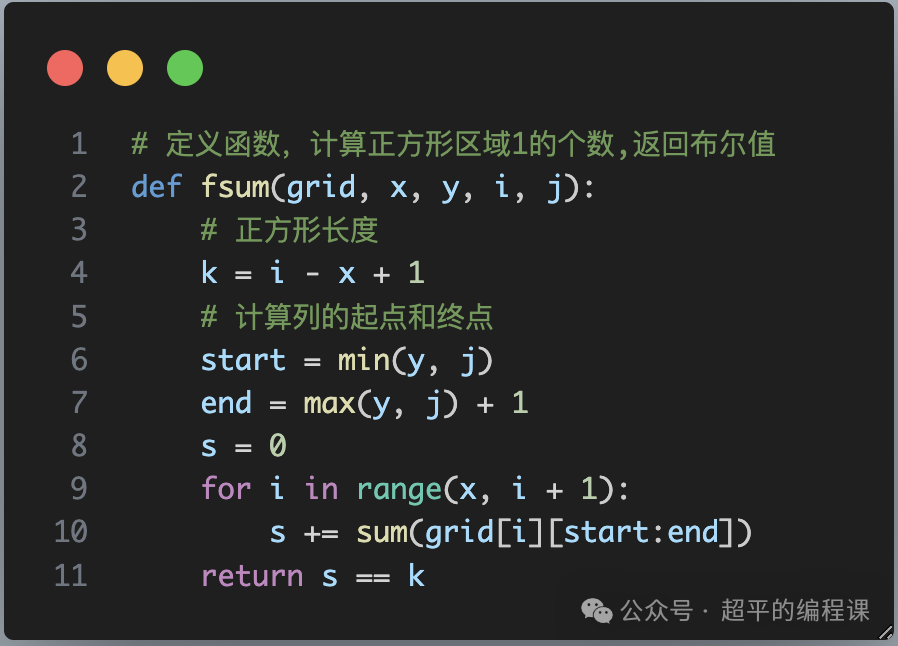
简单说明4点：

1). grid是输入的二维列表，x和y是指正方形对角线的起点，i和j是正方形对角线的终点；

2). 通过i和x来计算正方形的长度；

3). 对于一个正方形区域而言，要取k行k列数据，计算1的个数，grid本身是一个二维列表，只需要计算列的起点和终点，运用切片运算就可以，但是由于存在撇和捺两条对角线，因此需要计算好列起点start和列终点end的值。

4). k是正方形的长度，如果整个正方形区域1的和等于k，说明满足条件，可以获得奖品，返回True，否则返回false。

b. 捺对角线DFS函数

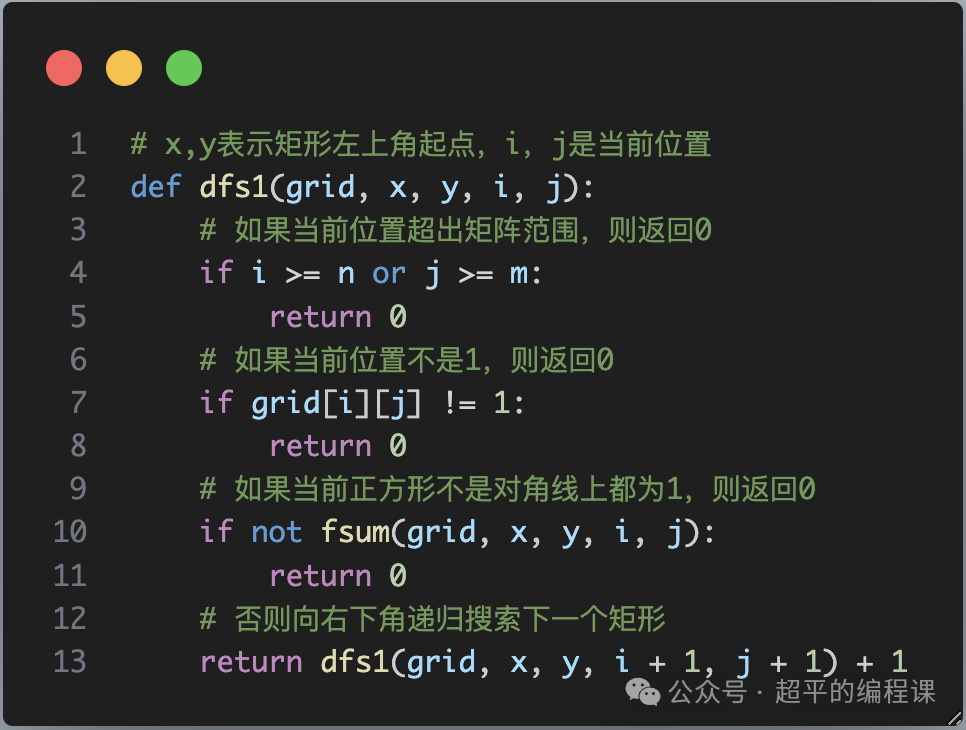
c. 撇对角线DFS函数

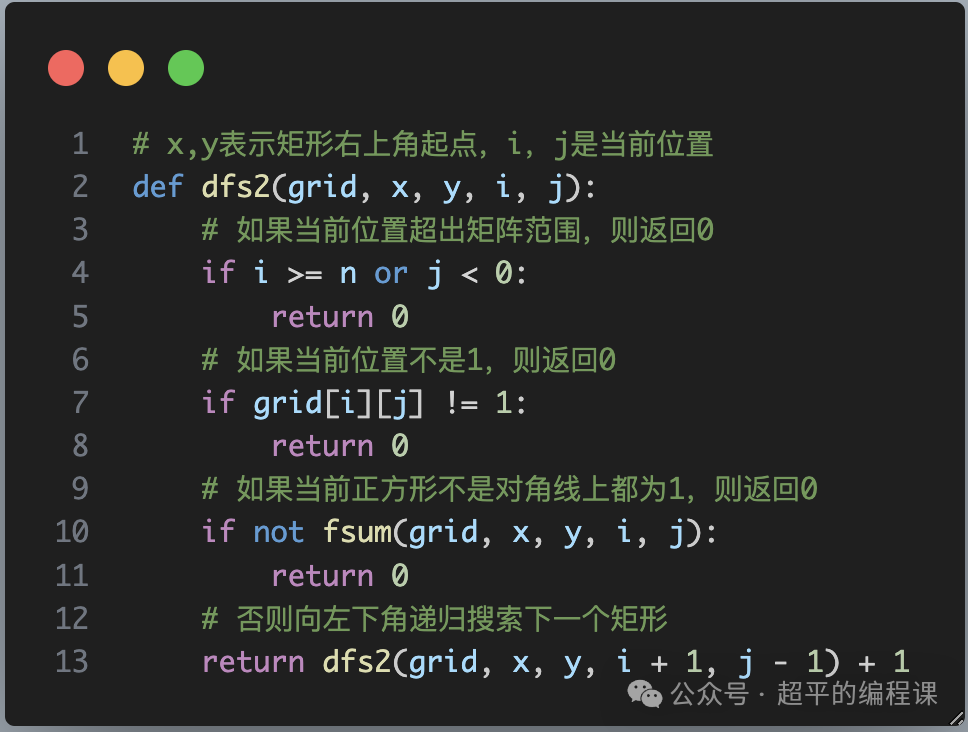
代码基本上差不多，强调两点：

1). 在进行DFS搜索时，有3个条件需要判断，一是越界，二是单元格的值不为0，三是所构成的正方形区域中1都在对角线上；

2). 注意这里x，y和i，j的作用和区别，i和j主要用于dfs搜索，而x和y则在计算正方形区域中1的数量时必不可少。

2 遍历矩阵计算最大值

有了上面的3个函数，接下来就好办了，先获取输入的数据，再遍历二维列表，计算并更新最大奖品数即可，具体代码如下：

代码不多，说明3点：

1). 首先需要获取用户输入的数据，将二维列表数据保存到grid中；

2). 对于每个单元格而言，其起点就是i和j，因此需要使用将它们的值分别赋值给x和y；

3). 对于每个单元格，都存在撇和捺两种情况，取二者中的较大值，并不断更新即可。

至此，整个程序就全部完成了，你可以输入不同的数据来测试效果啦。

四.总结与思考

本题代码在36行左右，涉及到的知识点包括：

• 循环语句；

• 条件语句；

• 二维列表；

• 自定义函数；

• DFS算法；

作为本次测评中高级最后一题，本题分值为100分，代码量较多，难度较大。关键点有两个，一是深入理解题目的意思，找到问题的规律和特点，二是通过自定义函数来简化代码。

二维列表是编程中常见的数据结构，对二维列表的遍历是学习编程的基本功，除了最简单的横向遍历和纵向遍历之外，还包括斜线遍历和螺旋遍历等，一定要多加练习，做到灵活运用。

超平老师给你留一道思考题，本题可以使用动态规划来实现吗，如果可以的话，代码该如何编写呢？

你还有什么好的想法和创意吗，也非常欢迎和超平老师分享探讨。

如果你觉得文章对你有帮助，别忘了点赞和转发，予人玫瑰，手有余香😄

需要源码的，可以移步至“超平的编程课”gzh。