1.M-P神经元
M-P神经元,全称为McCulloch-Pitts神经元,是一种数学模型,用于模拟生物神经元的功能。这个模型是由Warren McCulloch和Walter Pitts在1943年提出的。它是人工智能和计算神经科学领域中非常重要的早期模型。
M-P神经元接收n个输入(通常来自其他神经元),并给各个输入赋予权重计算加权和,然后和自身特有的阈值
θ
\theta
θ进行比较(作减法),最后经过激活函数(模拟“抑制”和“激活”)处理得到输出(通常是给下一个神经元)
y
=
f
(
∑
i
=
1
n
w
i
x
i
−
θ
)
=
f
(
w
T
x
+
b
)
y=f(\sum_{i=1}^nw_ix_i-\theta)=f(w^Tx+b)
y=f(i=1∑nwixi−θ)=f(wTx+b)
单个M-P神经元:感知机(sgn作激活函数)、对数几率回归(sigmoid作激活函数)
多个M-P神经元:神经网路
2.感知机(分类模型)
2.1 sgn函数
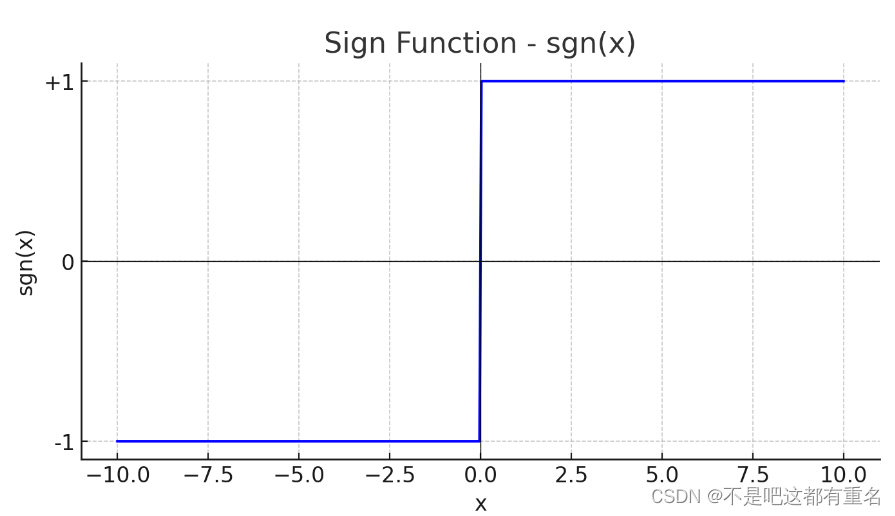
sgn 函数,或称为符号函数(sign function):是一个数学函数,用于确定一个实数的符号。sgn 函数的定义如下:
- 当x>0时,sgn(x)=1
- 当x=0时,sgn(x)=0
- 当x<0时,sgn(x)=-1
图像如下:
2.2 感知机
1)模型
其具体公式如下:
y
=
s
g
n
(
w
T
w
−
θ
)
=
{
1
,
w
T
x
−
θ
>
=
0
0
,
w
T
x
−
θ
<
0
y=sgn(w^Tw-\theta) =\begin{cases} 1& ,{w^Tx-\theta>= 0}\\ 0& ,{w^Tx-\theta<0} \end{cases}
y=sgn(wTw−θ)={10,wTx−θ>=0,wTx−θ<0
其中,
x
∈
R
N
x\in \mathbb{R}^N
x∈RN为样本的特征向量,是感知机模型的输入,
w
,
θ
w,\theta
w,θ是感知机模型的参数,
w
∈
R
n
w\in \mathbb{R}^n
w∈Rn为权重,
θ
\theta
θ 为阈值
从几何的角度来说,给定一个线性可分的数据集T,感知机的学习目标是求得能对数据集T中的正负样本完全正确划分的超平面,其中
w
T
x
−
θ
w^Tx-\theta
wTx−θ即为超平面方程。
n维空间的超平面
(
w
T
x
+
b
=
0
,
其中
w
,
x
∈
R
n
)
(w^Tx+b=0,其中w,x \in \mathbb R^n)
(wTx+b=0,其中w,x∈Rn):
- 超平面方程不唯一
- 法向量w垂直于超平面
- 法向量w和位移项b确定一个唯一超平面
- 法向量w指向的那一半空间为正空间,另一半为负空间
缺点: 只能解决线性可分的问题
模型图如下所示,只包含一个输入层和一个输出层。

2)策略
感知机的学习策略是,随机初始化
w
,
b
w,b
w,b,将全体训练样本带入模型找出误分类样本,假设此时误分类样本的集合为
M
⊆
T
M\subseteq T
M⊆T对任意一个误分类样本
(
x
,
y
)
∈
M
(x,y)\in M
(x,y)∈M来说,当
w
T
x
−
θ
>
=
0
w^Tx-\theta >=0
wTx−θ>=0时,模型输出值为
y
^
=
1
\hat y=1
y^=1,样本真实标记为y=0;繁殖,当
w
T
x
−
θ
<
0
w^Tx-\theta<0
wTx−θ<0时,模型输出值为
y
^
\hat y
y^=0,样本真实标记为y=1。综合两种情况可知,以下公式恒成立
(
y
^
−
y
)
(
w
T
x
−
θ
)
>
=
0
(\hat y-y)(w^Tx-\theta)>=0
(y^−y)(wTx−θ)>=0
所以,给定数据集T,其损失函数可以定义为:
L
(
w
,
θ
)
=
∑
x
∈
M
(
y
^
−
y
)
(
w
T
x
−
θ
)
L(w,\theta)=\sum_{x\in M}(\hat y-y)(w^Tx-\theta)
L(w,θ)=x∈M∑(y^−y)(wTx−θ)
此时损失函数是非负的。如果没有误分类点,损失函数值为0.而且,误分类点越少,误分类点离超平面越近,损失函数值就越小。
损失函数还可以进一步优化,将
θ
\theta
θ并入
w
w
w向量中成为第n+1维0,其中x的第n+1维恒为-1。那么损失函数进一步简化为:
L
(
w
)
=
∑
x
∈
M
(
y
^
−
y
)
w
T
x
L(w)=\sum_{x\in M}(\hat y-y)w^Tx
L(w)=x∈M∑(y^−y)wTx
3)算法
当误分类样本集合M固定时,可以球的损失函数
L
(
w
)
L(w)
L(w)的梯度为
∇
w
L
(
w
)
=
∑
x
i
∈
M
(
y
^
i
−
y
i
)
x
i
\nabla_wL(w)=\sum_{x_i\in M}(\hat y_i-y_i)x_i
∇wL(w)=xi∈M∑(y^i−yi)xi
学习算法具体采用的是随机梯度下降法,也即极小化过程中不是一次使M中的所有误分类点的梯度下降,而是一次随机选取一个误分类点使其梯度下降。所以权重
w
w
w的更新公式为:
w
←
w
+
Δ
w
w \leftarrow w+\Delta w
w←w+Δw
Δ
w
=
−
η
(
y
^
i
−
y
i
)
x
i
=
η
(
y
i
−
y
^
i
)
x
i
\Delta w=-\eta(\hat y_i-y_i)x_i=\eta(y_i-\hat y_i)x_i
Δw=−η(y^i−yi)xi=η(yi−y^i)xi
其中
η
\eta
η为学习率,最终解出来的w通常不唯一。
从几何角度方便理解一点,如下图所示,

可以看到红线和绿线都可以把正负样本分开,它们代表了两组
w
w
w,因此说明解不唯一。
3.神经网络
为了解决线性不可分的数据集(其他的当个神经元的模型也可以结局线性不可分的数据集,只是感知机不可以),提出了由多个神经元构成的神经网络,且用通用近似定理可以证明:只需一个包含足够多神经元的隐层,多层前馈网络(最经典的神经网络之一)就能以任意精度逼近任意复杂度的连续函数。
优点:
既能做回归,也能做分类,而且不需要复杂的特征工程。
需要考虑的问题:
- 对于具体场景,神经网络该做多深,多宽?(没有理论支撑,都是实践经验)
- 对于具体场景,神经网络的结构该如何设计才最合理(没有强理论指导)
- 对于具体场景,神经网络的输出结果该如何解释?(模型的可解释性可以用来指导特征调整)
经典神经网络——多层前馈网络:
每层神经元与下一层神经元全互连,神经元之间不存在同层连接,也不存在跨层连接。

将神经网络(NN)看作一个特征加工函数
x
∈
R
d
→
N
N
(
x
)
→
y
=
x
∗
∈
R
l
x\in R^d \rightarrow NN(x) \rightarrow y=x^* \in R^l
x∈Rd→NN(x)→y=x∗∈Rl
回归:后面接一个
R
l
→
R
R^l \rightarrow R
Rl→R的 神经元
y
=
w
T
x
∗
+
b
y=w^Tx^*+b
y=wTx∗+b
分类:后面接一个
R
l
→
[
0
,
1
]
R^l \rightarrow [0,1]
Rl→[0,1]的神经元,例如激活函数为sigmoid函数的神经元
y
=
1
1
+
e
−
(
w
T
x
∗
+
b
)
y=\frac{1}{1+e^{-(w^Tx^*+b)}}
y=1+e−(wTx∗+b)1
神经网络可以自动提取特征不用人为的手工设计特征。
神经网络训练方法——BP算法:
在20世纪80年代之前,尽管神经网络已经存在一段时间,但其实际应用受到了限制,主要原因在于无法有效地训练多层神经网络。
在这个背景下,1986年,David E. Rumelhart, Geoffrey E. Hinton, 和 Ronald J. Williams在他们的论文《Learning representations by back-propagating errors》中提出了反向传播算法。这一算法为多层前馈神经网络的训练提供了一个有效的方法,使得神经网络可以在更多复杂问题上展现出强大的表现力。
BP算法是一种基于随机梯度下降的参数更新算法。反向传播算法在处理多层神经网络时,通过链式法则有效地计算梯度,而随机梯度下降则用于基于这些梯度更新权重。反向传播算法与随机梯度下降相辅相成,共同实现了多层神经网络的高效训练。
下面是以输入层第i个神经元与隐层第h个神经元之间的连接全
v
i
h
v_{ih}
vih为例推导一下:
损失函数
E
k
=
1
2
∑
j
=
1
l
(
y
^
j
k
−
y
j
k
)
2
E_k=\frac12\sum^l_{j=1}(\hat y^k_j-y^k_j)^2
Ek=21j=1∑l(y^jk−yjk)2
Δ
v
i
h
=
−
η
∂
E
k
∂
v
i
h
\Delta v_{ih}=-\eta \frac{\partial{E_k}}{\partial{v_{ih}}}
Δvih=−η∂vih∂Ek
用链式求导得到
∂
E
k
∂
v
i
h
=
∑
j
=
1
l
∂
E
k
∂
y
^
j
k
∗
∂
y
^
j
k
∂
β
j
∗
∂
β
j
∂
b
h
∗
∂
b
h
∂
α
h
∗
∂
α
h
∂
v
i
h
\frac{\partial{E_k}}{\partial{v_{ih}}}=\sum^l_{j=1}\frac{\partial{E_k}}{\partial{\hat y^k_j}}*\frac{\partial{\hat y^k_j}}{\partial{\beta_j }}*\frac{\partial{\beta_j }}{\partial{b_h}}*\frac{\partial{b_h}}{\partial{\alpha_h}}*\frac{\partial{\alpha_h}}{\partial{v_{ih}}}
∂vih∂Ek=j=1∑l∂y^jk∂Ek∗∂βj∂y^jk∗∂bh∂βj∗∂αh∂bh∗∂vih∂αh