Deformable Attention学习笔记
Vision Transformer with Deformable Attention
Abstract
Transformer 最近在各种视觉任务中表现出卓越的表现。大的(有时甚至是全局的)接受域使Transformer模型比CNN模型具有更高的表示能力。然而,单纯扩大接受野也会引起一些问题。一方面,在ViT中使用密集注意力会导致过多的内存和计算成本,特征会受到超出感兴趣区域的无关部分的影响。另一方面,PVT或Swin Transformer中采用的稀疏注意是数据不可知的,可能会限制建模远程关系的能力。为了解决这些问题,我们提出了一种新的Deformable 自注意模块,该模块以数据依赖的方式选择自注意中的键对和值对的位置。这种灵活的方案使自我注意模块能够专注于相关区域,并捕捉到更多的信息特征。在此基础上,我们提出了Deformable 注意变压器,一个具有Deformable 注意的通用骨干模型,用于图像分类和密集预测任务。大量的实验表明,我们的模型在综合基准测试中取得了持续改进的结果。代码可从https://github.com/LeapLabTHU/DAT获得。
1. Introduction
最初引入Transformer[34]是为了解决自然语言处理任务。近年来在计算机视觉领域显示出了巨大的潜力[12,26,36]。先锋工作Vision Transformer [12] (ViT)堆叠多个Transformer块,以处理不重叠的图像补丁(即可视标记)序列,导致了图像分类的无卷积模型。与CNN的同类模型相比[18,19],基于transformer的模型具有更大的接受域,并擅长于建模远程依赖关系,这被证明在大量训练数据和模型的情况下能够获得更好的性能模型参数。然而,视觉识别中过多的注意是一把双刃剑,存在诸多弊端。具体来说,每个查询补丁要参加的键的数量过多会产生较高的计算成本和较慢的收敛速度,并增加过拟合的风险。
为了避免过度的注意力计算,已有的研究[6,11,26,36,43,49]利用精心设计的有效注意力模式来降低计算复杂度。Swin Transformer[26]采用了基于windows的本地注意限制局部窗口的注意,而金字塔视觉转换器(PVT)[36]下采样键和值特征映射以节省计算。虽然有效,但手工制作的注意力模式与数据无关,可能不是最佳的。很可能相关的键/值被删除,而不太重要的键/值仍然保留。
理想情况下,人们会期望给定查询的候选键/值集是灵活的,并且能够适应每个单独的输入,这样手工制作的稀疏注意模式中的问题就可以得到缓解。事实上,在cnn的文献中,学习卷积滤波器的Deformable 接受场已被证明在数据依赖的基础上有选择地关注信息更多的区域[9]是有效的。最著名的工作,变形卷积网络[9],在许多具有挑战性的视觉任务中产生了令人印象深刻的结果。这促使我们在Vision Transformers中探索一种Deformable 注意模式。然而,这种想法的幼稚实现导致了不合理的高内存/计算复杂度:由Deformable 偏移引入的开销是补丁数量的二次函数。因此,尽管最近的一些工作[7,46,54]研究了Vision Transformers中Deformable 机构的思想,但由于计算成本高,没有一项工作将其作为构建像DCN这样强大的骨干网的基本构件。相反,它们的变形机制要么被采用在检测头[54]中,要么被用作预处理层,为后续骨干网[7]采样补丁。
本文提出了一种简单、高效的Deformable 自注意模块,并在该模块上构造了一个强大的金字塔骨架——Deformable 注意变压器(DA T),用于图像分类和各种密集预测任务。与DCN对整个特征图中的不同像素学习不同的偏移量不同,我们建议学习几组查询不可知偏移量,以将键和值转移到重要区域(如图1(d)所示),这是基于[3,52]中的观察,即对于不同的查询,全局注意通常会导致几乎相同的注意模式。这个设计既保持了线性的空间复杂性,又引入了变形的注意模式到Transformer的主干。具体来说,对于每个注意模块,参考点首先生成为统一的网格,这些网格在输入数据中是相同的。然后,偏移网络以查询特征为输入,为所有参考点生成相应的偏移量。通过这种方式,候选键/值被转移到重要的区域,从而以更高的灵活性和效率增强了原始的自我注意模块,以捕获更多信息的特征。
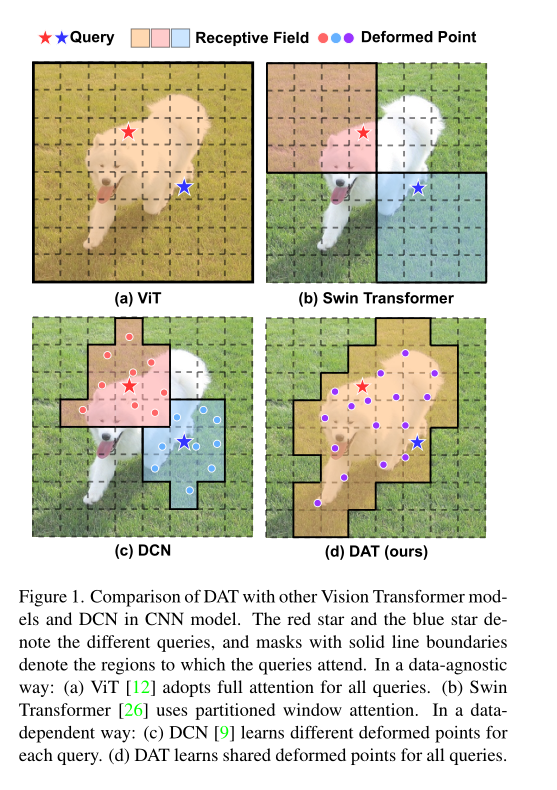
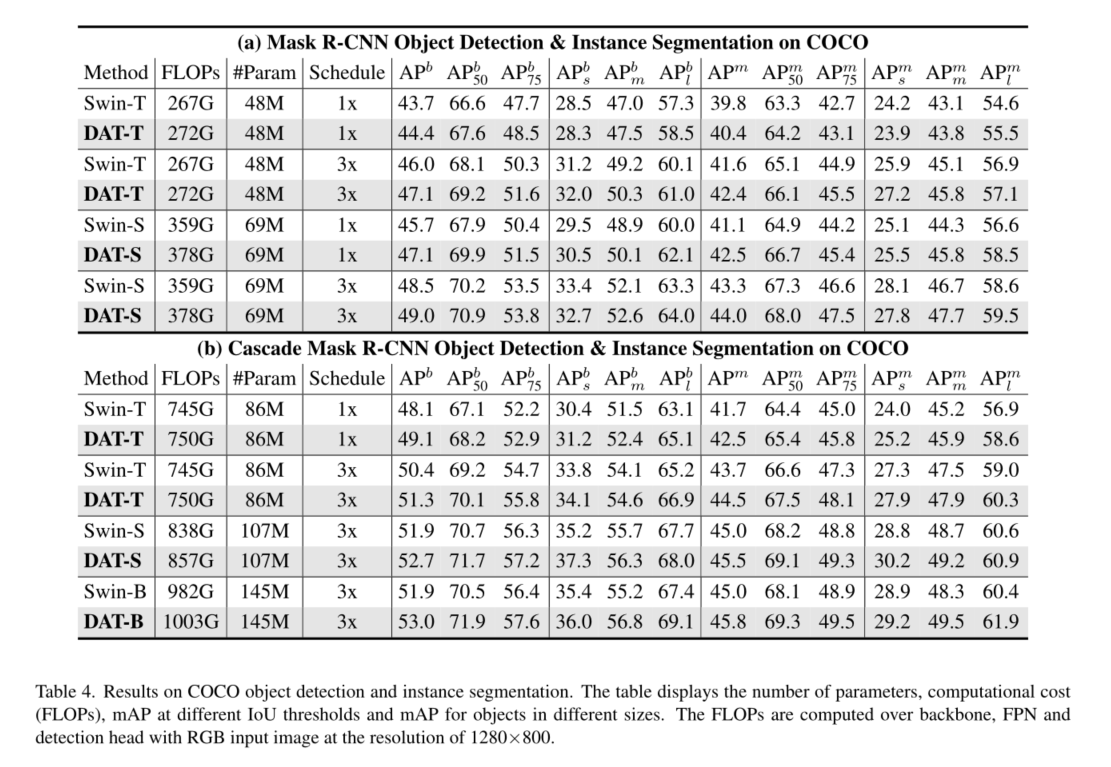
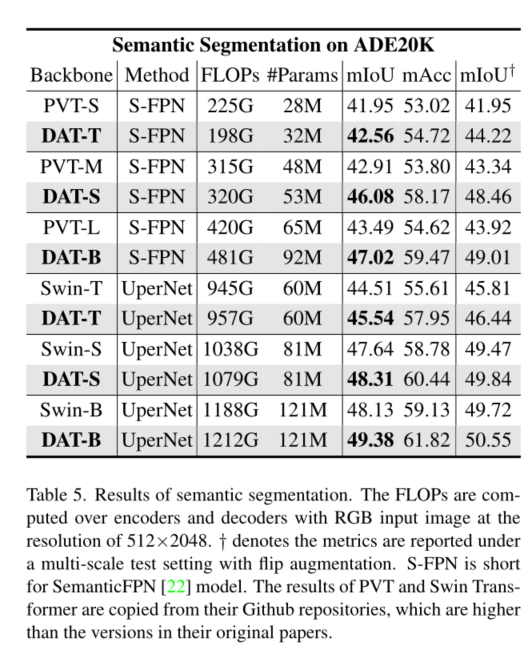
综上所述,我们的贡献如下:我们提出了视觉识别的第一个Deformable 自我注意中枢,其中数据依赖的注意模式具有较高的灵活性和效率。在ImageNet[10]、ADE20K[51]和COCO[25]上的大量实验表明,我们的模型始终优于包括Swin Transformer在内的竞争基线,在图像分类的前1精度上有0.7的差距,在语义分割的mIoU上有1.2的差距,在盒AP和掩码AP的对象检测上有1.1的差距。在小对象和大对象上的优势更明显,差距为2.1。
2. Related Work
Transformer vision backbone
自引入ViT[12]以来,改进[6,11,26,28,36,43,49]的重点是学习密集预测任务的多尺度特征和有效的注意机制。这些注意机制包括窗口注意[11,26]、全局令牌[6,21,32]、集中注意[43]和动态令牌大小[37]。最近,基于卷积的方法被引入到Vision Transformer模型中。其中,已有研究侧重于用卷积运算对变压器模型进行补充,引入额外的归纳偏差。CvT[39]在令牌化过程中采用了卷积,并利用stride卷积降低了自注意的计算复杂度。带卷积梗[41]的ViT提出在早期增加卷积,以达到更稳定的训练。CSwin Transformer[11]采用了基于卷积的位置编码技术,并显示了对下游任务的改进。许多基于卷积的技术可以应用在DAT之上,以进一步提高性能。
Deformable CNN and attention
Deformable 卷积[9,53]是一种处理以输入数据为条件的灵活空间位置的强大机制。最近,它已被应用于视觉变压器[7,46,54]。Deformable DETR[54]通过为CNN骨干网顶部的每个查询选择少量键来提高DETR[4]的收敛性。它的变形注意力不适合用于特征提取的视觉主干,因为缺少键限制了表示能力。此外,在Deformable DETR中的注意力来自简单的学习线性投影和键不在查询令牌之间共享。DPT[7]和PS-ViT[46]构建Deformable 模块来优化可视标记。具体来说,DPT提出了一种Deformable 补丁嵌入来改进跨阶段的补丁,PS-ViT在ViT主干之前引入了一个空间采样模块,以改进可视化令牌。它们都没有将Deformable 注意力纳入视觉中枢。相比之下,我们的变形注意力需要一个强大而简单的设计来学习一组视觉标记之间共享的全局键,并可被采用为各种视觉任务的一般主干。我们的方法也可以看作是一种空间自适应机制,已经在各种著作中被证明是有效的[16,38]。
3. Deformable Attention Transformer
3.1. Preliminaries
我们首先回顾最近的Vision Transformers中的注意机制。取一个扁平化的特征映射 x ∈ R N × C x∈R^{N×C} x∈RN×C作为输入,M个头的多头自注意块(MHSA)可表示为
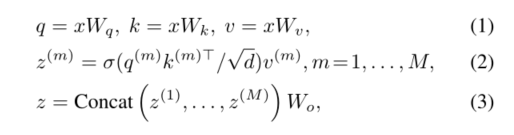
其中σ(·)为softmax函数,d = C/M为每个头的尺寸。z(m)表示第m个注意头的嵌入输出, q ( m ) , k ( m ) , v ( m ) ∈ R N × d q^{(m)}, k^{(m)}, v^{(m)}∈R^{N×d} q(m),k(m),v(m)∈RN×d分别表示查询、键和值的嵌入。 W q , W k , W v , W o ∈ R C × C W_q, W_k, W_v, W_o∈R^{C×C} Wq,Wk,Wv,Wo∈RC×C为投影矩阵。为了构建一个Transformer块,通常采用具有两个线性转换和一个GELU激活的MLP块来提供非线性。
通过归一化层和标识快捷方式,第l个Transformer块被表述为
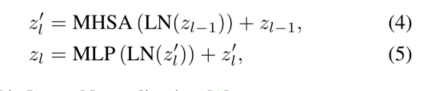
LN是层归一化[1]。
3.2. Deformable Attention
现有的分级视觉变压器,特别是PVT[36]和Swin变压器[26]试图解决过度关注的挑战。前者的下采样技术导致严重的信息丢失,后者的注意力转移导致接受域的增长非常缓慢,这限制了建模大型对象的潜力。因此,需要依赖数据的稀疏注意来灵活建模相关特征,导致DCN[9]首先提出了变形机制。然而,简单地在Transformer模型中实现DCN不是一个简单的问题。在宽带,每个元素特征映射学习其单独补偿,一个3×3的可变形的卷积地图上一个W×H×C特性的空间复杂性9HWC .如果我们直接应用相同的注意机制模块,空间复杂度将大大 N q N k C N_qN_kC NqNkC, N q 、 N k N_q、N_k Nq、Nk查询和钥匙的数量,通常有相同的尺度特性HW地图大小,将大约四次的复杂性。尽管变形DETR[54]通过在每个刻度上设置较低数量的 N k = 4 N_k = 4 Nk=4的键来设法减少这种开销,并作为检测头工作得很好,但由于不可接受的信息丢失,它不如在骨干网中处理这么少的键(参见附录中的详细比较)。同时,文献[3,52]的观察发现,不同的查询在视觉注意模型中具有相似的注意地图。因此,我们选择一个更简单的解决方案,为每个查询共享移位的键和值,以实现有效的折衷。
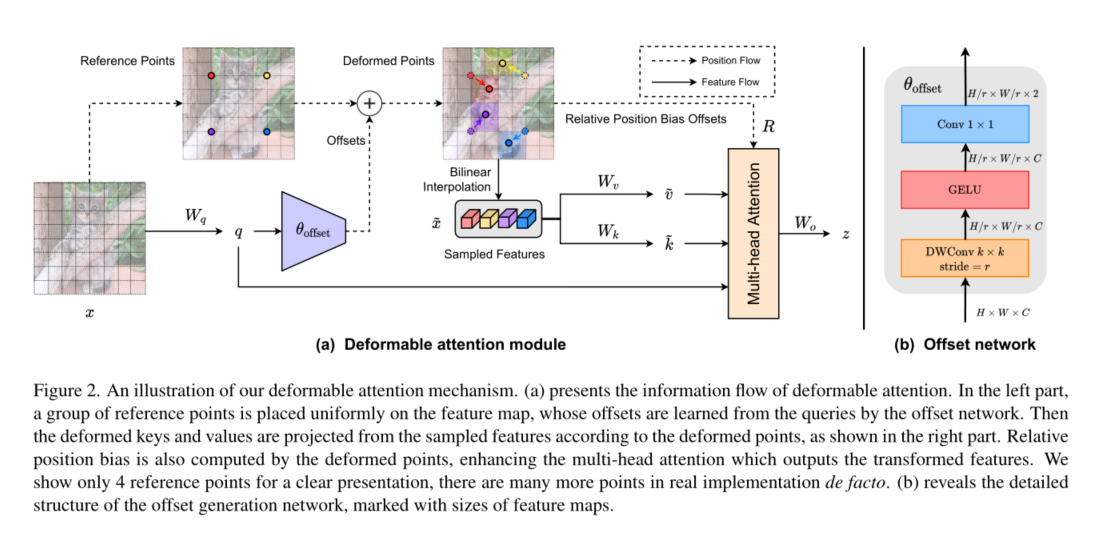
具体而言,我们提出了在特征图中重要区域的指导下,利用变形注意有效地建模标记之间的关系。这些聚焦区域由多组变形采样点确定,这些采样点由偏移网络从查询中学习到。我们采用双线性插值的方法对特征进行采样然后将采样的特征输入到键和值投影中,得到变形的键和值。最后,应用标准的多头注意对采样键进行查询,并从变形值中聚合特征。此外,变形点的位置提供了更强大的相对位置偏差,以促进变形注意的学习,这将在接下来的章节中讨论。
Deformable attention module
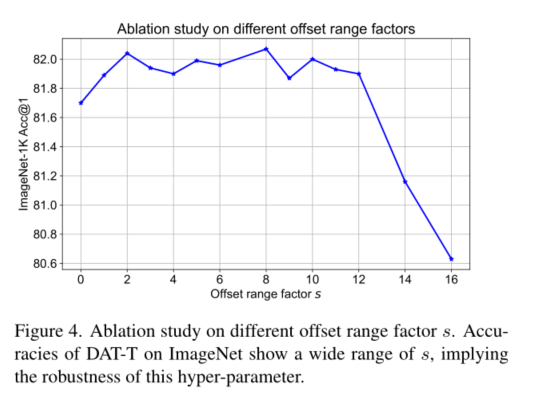
如图2(a)所示,给定输入特征映射 x ∈ R H × W × C x∈R^{H×W ×C} x∈RH×W×C,生成一个由点 p ∈ R H G × W G × 2 p∈R^{H_G×W_G×2} p∈RHG×WG×2组成的统一网格作为参考。具体来说,网格大小从输入特征映射大小中下采样r, H G = H / r , W G = W / r H_G = H/r, W_G = W/r HG=H/r,WG=W/r。参考点的值是线性间隔的二维坐标 ( 0 , 0 ) , … , ( H G − 1 , W G − 1 ) {(0,0),…, (H_G−1,W_G−1)} (0,0),…,(HG−1,WG−1),然后根据网格形状 H G × W G H_G × W_G HG×WG归一化到[−1,+1]的范围内,其中(−1,−1)表示左上角,(+1,+1)表示右下角。为了获得每个参考点的偏移量,将特征图线性投影到查询令牌 q = x W q q =xW_q q=xWq,然后将特征图馈入一个轻量级子网络 θ o f f s e t ( ⋅ ) θ_{offset}(·) θoffset(⋅),生成偏移量 ∆ p = θ o f f s e t ( q ) ∆p = θ_{offset}(q) ∆p=θoffset(q)。为了稳定训练过程,我们将∆p的幅值按一些预定义的因子s进行缩放,以防止偏移量过大,即 ∆ p ← s t a n h ( ∆ p ) ∆p← s tanh(∆p) ∆p←stanh(∆p)。然后在变形点的位置采样特征作为键和值,然后得到投影矩阵:
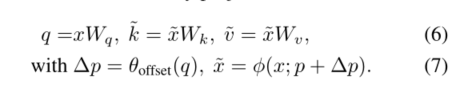
k ~ \tilde{k} k~和 v ~ \tilde{v} v~分别代表变形的键和值嵌入。具体来说,我们设置了采样函数φ(·;·)转化为双线性插值,使其可微:
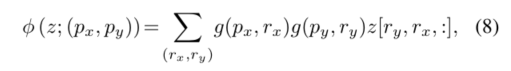
其中 g ( a , b ) = m a x ( 0 , 1 − ∣ a − b ∣ ) g(a, b) = max(0,1−|a−b|) g(a,b)=max(0,1−∣a−b∣)和 ( r x , r y ) (r_x, r_y) (rx,ry)索引 z ∈ R H × W × C z∈R^{H×W ×C} z∈RH×W×C上的所有位置。因为g只在最接近 ( p x , p y ) (p_x, p_y) (px,py)的4个积分点上是非零的,它将式(8)简化为4个位置的加权平均值。与现有方法类似,我们对q、k、v执行多头注意,并采用相对位置偏移量r。为:
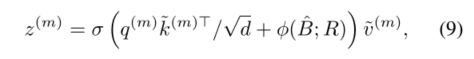
其中 ϕ ( B ^ ; R ) ∈ R H W × H G W G \phi(\hat{B} ; R) \in \mathbb{R}^{H W \times H_{G} W_{G}} ϕ(B^;R)∈RHW×HGWG对应前面工作[26]之后的位置嵌入,同时有一些改编。详细信息将在本节后面解释。将每个头的特征连接在一起,通过 W o W_o Wo进行投影,得到最终的输出z,即式(3)。
Offset generation
如前所述,偏移生成采用一个子网络,该子网络消耗查询特征并分别输出参考点的偏移值。考虑到每个参考点覆盖一个局部s × s区域(s为偏移量的最大值),生成网络还应具有对局部特征的感知,以学习合理的偏移量。因此,我们将子网络实现为两个具有非线性激活的卷积模块,如图2(b)所示。输入特征首先通过5×5深度卷积来捕获局部特征。然后采用GELU激活和1×1卷积得到二维偏移量。同样值得注意的是,1 × 1卷积中的偏差被降低,以减轻所有位置的强制移位。
Offset groups
为了促进变形点的多样性,我们在MHSA中遵循类似的范式,将特征通道分成G组。每个组的特征使用共享子网络分别生成相应的偏移量。在实际操作中,将注意模块的头号M设置为偏移组G大小的数倍,确保将多个注意头分配给一组变形的键和值。
Deformable relative position bias
相对位置偏差对每对查询和键之间的相对位置进行编码,用空间信息增强了香草注意。考虑形状为H×W的特征图,其二维相对坐标位移分别在[−H, H]和[−W, W]的范围内。在Swin Transformer[26]中,构造相对位置偏差表 B ∈ R ( 2 H − 1 ) × ( 2 W − 1 ) B∈R^{(2H−1)×(2W−1)} B∈R(2H−1)×(2W−1),将该表与两个方向的相对位移标度,得到相对位置偏差B。因为我们的可变形的注意力已经连续键的位置,计算归一化范围的相对位移(−1,+ 1),然后插入 φ ( B ^ ; R ) φ(\hat{B};R) φ(B^;R)在参数化偏置表中,以连续的相对位移为例,将 B ∈ R ( 2 H − 1 ) × ( 2 W − 1 ) B∈R^{(2H−1)×(2W−1)} B∈R(2H−1)×(2W−1),以覆盖所有可能的偏移值。
Computational complexity
可变形多头注意(DMHA)的计算成本与PVT或Swin变压器相似。唯一的额外开销来自于用于生成偏移量的子网络。整个模块的复杂度可以总结为:

其中 N s = H G W G = H W / r 2 N_s = H_G W_G = HW/r^2 Ns=HGWG=HW/r2为采样点数。可以看出,偏移网络的计算代价具有线性复杂度w.r .t。通道大小,相对于注意计算的成本来说是次要的。通常,考虑Swin-T[26]模型的第三阶段图像分类,其中H = W = 14, Ns = 49, C = 384,单个块中注意模块的计算成本为79.63M FLOPs。如果配备了我们的变形模组(k = 5),条件开销为5.08M Flops,仅占整个模块的6.0%。此外,通过选择一个大的下样本因子r,可以进一步降低复杂度,这使得它适合于具有更高分辨率输入的任务,如对象检测和实例分割。
3.3. Model Architectures
我们用Transformer (Eq.(4))中的可变形注意替换了普通的MHSA,并将其与MLP (Eq.(5))相结合,构建了一个可变形的视觉变压器块。在网络架构方面,我们的变形注意变压器模型与[7,26,31,36]具有类似的金字塔结构,广泛适用于需要多尺度特征映射的各种视觉任务。如图3所示,首先对形状为H × W × 3的输入图像进行步幅为4的4×4非重叠卷积嵌入,然后进行归一化层,得到 h / 4 × w / 4 × C h/4 × w/4 × C h/4×w/4×C的斑块嵌入。以构建分层特征金字塔为目标,主干包括四个阶段,步幅逐渐增大。在两个连续的阶段之间,有一个不重叠的2×2卷积,使用stride 2对特征映射进行下采样,使空间大小减半,特征维度翻倍。在分类任务中,我们首先对上一阶段输出的特征映射进行归一化处理,然后采用集合特征的线性分类器对对数进行预测。在目标检测、实例分割和语义分割等任务中,DAT在综合视觉模型中起着骨干作用,可提取多尺度特征。我们在每个阶段的特征中添加一个归一化层,然后将它们输入到以下模块中,如对象检测中的FPN[23]或语义分割中的解码器。
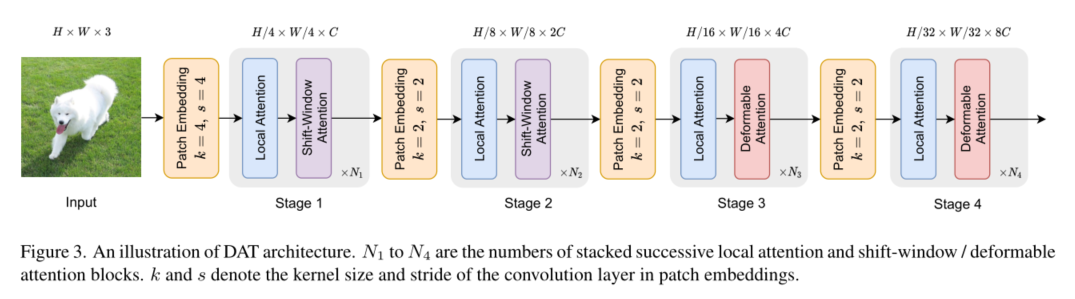
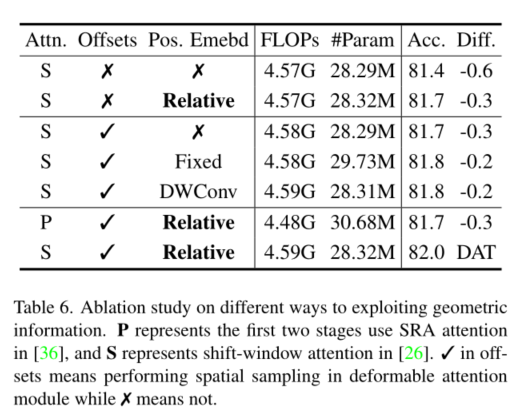
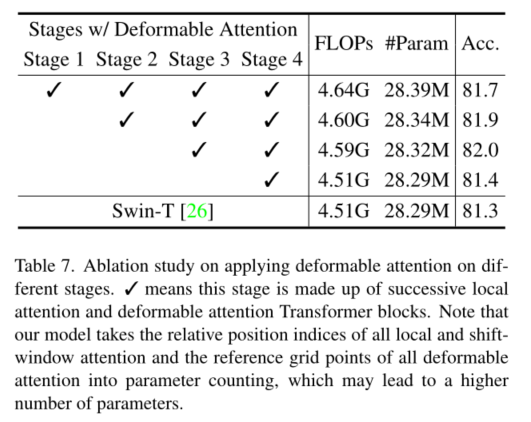
在DA t的第三和第四阶段引入连续的局部注意和可变形注意块。特征图首先由基于窗口的局部注意处理,进行局部信息聚合,然后通过可变形注意块对局部增强令牌之间的全局关系进行建模。这种带有局部和全局接受场的注意块交替设计有助于模型学习强表示,在GLiT [5], TNT[15]和Pointformer [29]. 由于前两个阶段主要学习局部特征,因此在这两个早期阶段不太喜欢变形注意。此外,前两阶段的键和值具有较大的空间大小,这大大增加了变形注意中的点积和双线性插值的计算开销。因此,为了实现模型容量和计算负担之间的权衡,我们只在第三和第四阶段放置可变形注意,并采用Swin Transformer[26]中的shift-window注意在早期阶段有更好的表示。我们在不同的参数和flop中构建了DA T的三个变体,以便与其他Vision Transformer模型进行公平的比较。我们在第三阶段通过堆叠更多块和增加隐藏维度来改变模型大小。详细的体系结构如表1所示。注意,DAT的前两个阶段还有其他的设计选择,例如pvt中的SRA模块。我们在表7中显示了比较结果。

4. Experiments
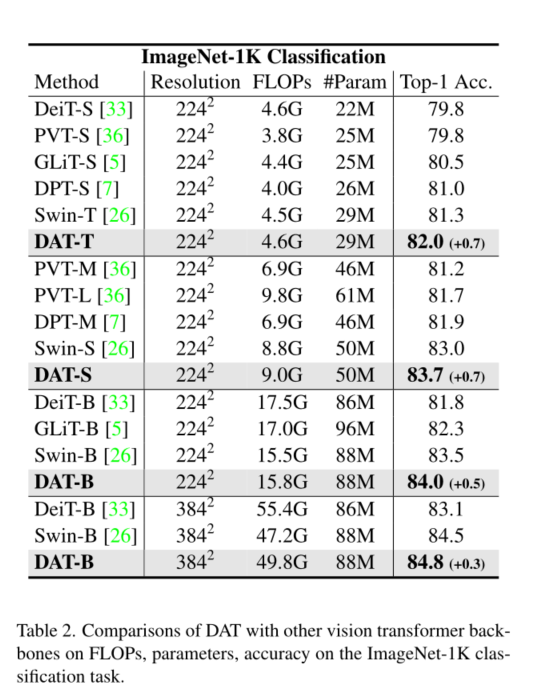
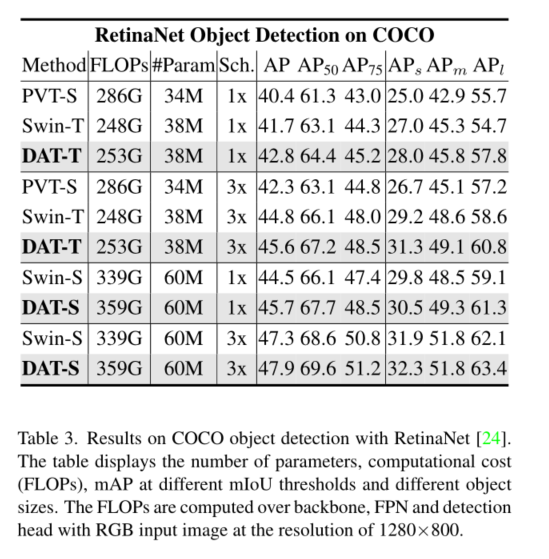

5. Conclusion
本文提出了一种可变形注意变压器,它是一种既适用于图像分类又适用于密集预测任务的新型分层视觉变压器。通过可变形注意模块,我们的模型能够以数据依赖的方式学习稀疏注意模式,并建模几何变换。大量的实验证明了我们的模型在竞争基线上的有效性。我们希望我们的工作能够启发人们设计灵活的注意力技巧。
代码
class DAttentionBaseline(nn.Module):
def __init__(
self, q_size, kv_size, n_heads, n_head_channels, n_groups,
attn_drop, proj_drop, stride,
offset_range_factor, use_pe, dwc_pe,
no_off, fixed_pe, stage_idx
):
super().__init__()
self.dwc_pe = dwc_pe
self.n_head_channels = n_head_channels
self.scale = self.n_head_channels ** -0.5
self.n_heads = n_heads
self.q_h, self.q_w = q_size
self.kv_h, self.kv_w = kv_size
self.nc = n_head_channels * n_heads
self.n_groups = n_groups
self.n_group_channels = self.nc // self.n_groups
self.n_group_heads = self.n_heads // self.n_groups
self.use_pe = use_pe
self.fixed_pe = fixed_pe
self.no_off = no_off
self.offset_range_factor = offset_range_factor
ksizes = [9, 7, 5, 3]
kk = ksizes[stage_idx]
self.conv_offset = nn.Sequential(
nn.Conv2d(self.n_group_channels, self.n_group_channels, kk, stride, kk//2, groups=self.n_group_channels),
LayerNormProxy(self.n_group_channels),
nn.GELU(),
nn.Conv2d(self.n_group_channels, 2, 1, 1, 0, bias=False)
)
self.proj_q = nn.Conv2d(
self.nc, self.nc,
kernel_size=1, stride=1, padding=0
)
self.proj_k = nn.Conv2d(
self.nc, self.nc,
kernel_size=1, stride=1, padding=0
)
self.proj_v = nn.Conv2d(
self.nc, self.nc,
kernel_size=1, stride=1, padding=0
)
self.proj_out = nn.Conv2d(
self.nc, self.nc,
kernel_size=1, stride=1, padding=0
)
self.proj_drop = nn.Dropout(proj_drop, inplace=True)
self.attn_drop = nn.Dropout(attn_drop, inplace=True)
if self.use_pe:
if self.dwc_pe:
self.rpe_table = nn.Conv2d(self.nc, self.nc,
kernel_size=3, stride=1, padding=1, groups=self.nc)
elif self.fixed_pe:
self.rpe_table = nn.Parameter(
torch.zeros(self.n_heads, self.q_h * self.q_w, self.kv_h * self.kv_w)
)
trunc_normal_(self.rpe_table, std=0.01)
else:
self.rpe_table = nn.Parameter(
torch.zeros(self.n_heads, self.kv_h * 2 - 1, self.kv_w * 2 - 1)
)
trunc_normal_(self.rpe_table, std=0.01)
else:
self.rpe_table = None
@torch.no_grad()
def _get_ref_points(self, H_key, W_key, B, dtype, device):
ref_y, ref_x = torch.meshgrid(
torch.linspace(0.5, H_key - 0.5, H_key, dtype=dtype, device=device),
torch.linspace(0.5, W_key - 0.5, W_key, dtype=dtype, device=device)
)
ref = torch.stack((ref_y, ref_x), -1)
ref[..., 1].div_(W_key).mul_(2).sub_(1)
ref[..., 0].div_(H_key).mul_(2).sub_(1)
ref = ref[None, ...].expand(B * self.n_groups, -1, -1, -1) # B * g H W 2
return ref
def forward(self, x):
B, C, H, W = x.size()
dtype, device = x.dtype, x.device
q = self.proj_q(x)
q_off = einops.rearrange(q, 'b (g c) h w -> (b g) c h w', g=self.n_groups, c=self.n_group_channels)
offset = self.conv_offset(q_off) # B * g 2 Hg Wg
Hk, Wk = offset.size(2), offset.size(3)
n_sample = Hk * Wk
if self.offset_range_factor > 0:
offset_range = torch.tensor([1.0 / Hk, 1.0 / Wk], device=device).reshape(1, 2, 1, 1)
offset = offset.tanh().mul(offset_range).mul(self.offset_range_factor)
offset = einops.rearrange(offset, 'b p h w -> b h w p')
reference = self._get_ref_points(Hk, Wk, B, dtype, device)
if self.no_off:
offset = offset.fill(0.0)
if self.offset_range_factor >= 0:
pos = offset + reference
else:
pos = (offset + reference).tanh()
x_sampled = F.grid_sample(
input=x.reshape(B * self.n_groups, self.n_group_channels, H, W),
grid=pos[..., (1, 0)], # y, x -> x, y
mode='bilinear', align_corners=True) # B * g, Cg, Hg, Wg
x_sampled = x_sampled.reshape(B, C, 1, n_sample)
q = q.reshape(B * self.n_heads, self.n_head_channels, H * W)
k = self.proj_k(x_sampled).reshape(B * self.n_heads, self.n_head_channels, n_sample)
v = self.proj_v(x_sampled).reshape(B * self.n_heads, self.n_head_channels, n_sample)
attn = torch.einsum('b c m, b c n -> b m n', q, k) # B * h, HW, Ns
attn = attn.mul(self.scale)
if self.use_pe:
if self.dwc_pe:
residual_lepe = self.rpe_table(q.reshape(B, C, H, W)).reshape(B * self.n_heads, self.n_head_channels, H * W)
elif self.fixed_pe:
rpe_table = self.rpe_table
attn_bias = rpe_table[None, ...].expand(B, -1, -1, -1)
attn = attn + attn_bias.reshape(B * self.n_heads, H * W, self.n_sample)
else:
rpe_table = self.rpe_table
rpe_bias = rpe_table[None, ...].expand(B, -1, -1, -1)
q_grid = self._get_ref_points(H, W, B, dtype, device)
displacement = (q_grid.reshape(B * self.n_groups, H * W, 2).unsqueeze(2) - pos.reshape(B * self.n_groups, n_sample, 2).unsqueeze(1)).mul(0.5)
attn_bias = F.grid_sample(
input=rpe_bias.reshape(B * self.n_groups, self.n_group_heads, 2 * H - 1, 2 * W - 1),
grid=displacement[..., (1, 0)],
mode='bilinear', align_corners=True
) # B * g, h_g, HW, Ns
attn_bias = attn_bias.reshape(B * self.n_heads, H * W, n_sample)
attn = attn + attn_bias
attn = F.softmax(attn, dim=2)
attn = self.attn_drop(attn)
out = torch.einsum('b m n, b c n -> b c m', attn, v)
if self.use_pe and self.dwc_pe:
out = out + residual_lepe
out = out.reshape(B, C, H, W)
y = self.proj_drop(self.proj_out(out))
return y, pos.reshape(B, self.n_groups, Hk, Wk, 2), reference.reshape(B, self.n_groups, Hk, Wk, 2)

![[MQ] 延迟队列/延迟插件下载](https://img-blog.csdnimg.cn/b99d6bf018304443a8d908bde3387b27.png)