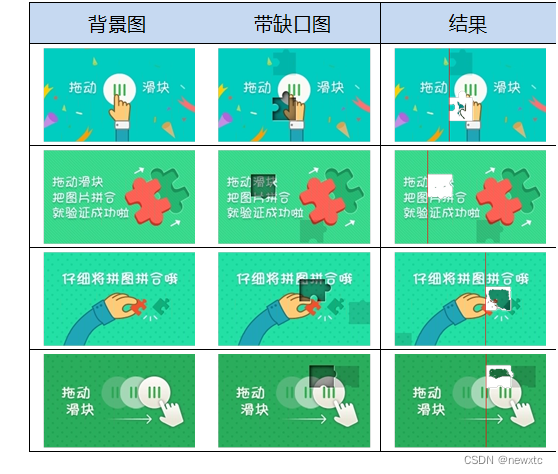
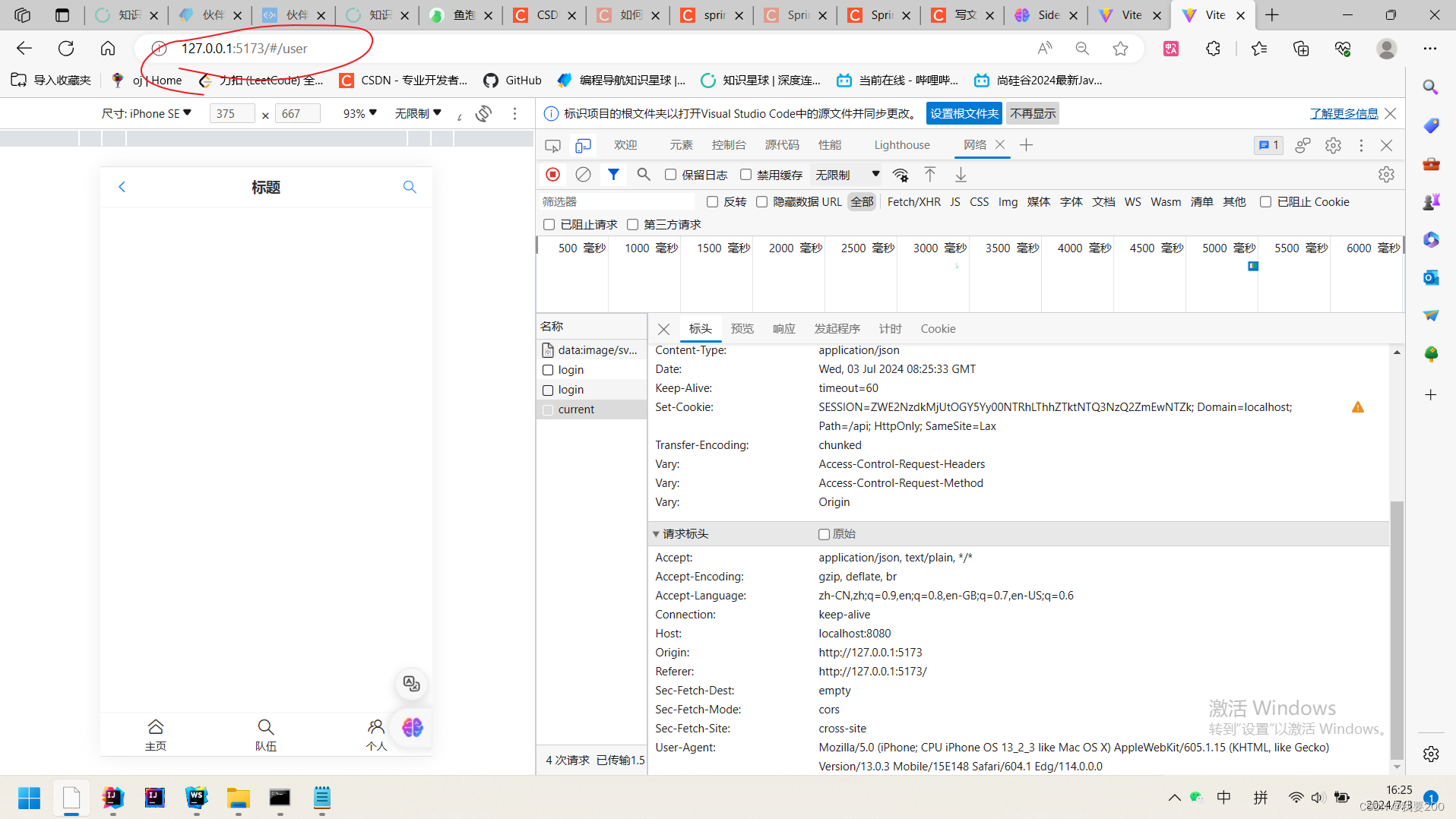
单层感知机模型


对于单层的感知机,它的激活函数是一个sigmoid
对于符号的定义做一个规范化,输入层每一层进行一个编号
输入是第0层,上标0表示属于输入层,下标0到n表示一共有n个节点(这里严格来说应该是0~n-1,为了书写方便,不区分),下标为i的意思就是第i个元素
中间层,包含权值、累加、激活函数的输出,权值上标还是表示第1层,有2个下标,第一个下标表示连接上一层 x i x_{i} xi的节点,第二个下标表示连接的是这一层的节点,由于此时这一层只有一个节点,所以总是为0
x 0 1 x_{0}^{1} x01,上标表示属于第一层,下标表示第一层上面的第几个元素,这里讨论的是单层感知机,所以第一层只有一个节点
x 1 0 x_{1}^{0} x10经过激活函数以后会得到一个输出值,把这个激活函数的输出值叫做 o 0 1 o_{0}^{1} o01
最后 o 0 1 o_{0}^{1} o01与目标值做均方差,即loss
推导一下单层感知机的推导公式

此处的σ(x)特指sigmoid函数,对x求导之后为σ(1-σ)
求导之前需要先向右计算一次所有的变量值,这就是前向传播
可以看出对哪一号节点求导, x j 0 x_{j}^{0} xj0就代表了哪一号节点的数值
对于单层的感知机可以很好的总结一下loss对某一号权值求导,最终仅仅跟这个神经元的输出节点 O 0 1 O_{0}^{1} O01以及跟他对应输入节点的数值有关系,可以通过这个公式非常简单的直接更新,也就是可以通过公式推导的过程计算出来每一条连接上面的梯度的大小然后直接更新
用pytorch计算,这里输入x的特征有10个

对loss做backward可以得到loss对w中的所有参数分别求偏导
多层感知机模型MLP以及梯度

输出节点变多了,均方差不是跟一个节点作比较,而是所有的输出跟所有的label做比较

一共有N×M个连接数量,因此有N×M个偏微分的计算
对i号节点的输出对t第i号节点的label做均方差, w j k w_{jk} wjk对 O k 1 O_{k}^{1} Ok1的影响只有当O的i等于k的时候 w j k w_{jk} wjk才会有连接,O的i为其他值的时候 w j k w_{jk} wjk是没有连接的,也就是偏导数为0
第四步的时候
x
k
1
x^{1}_{k}
xk1可以写成n个w和x相乘