#数据结构 笔记三

news2024/7/7 16:10:42

二叉树

1. 概念

二叉树Binary Tree是n个结点的有限集合。它或者是空集n=0，或者是由一个根结点以及两颗互不相交、分别称为左子树和右子树的二叉树组成。

二叉树与普通有序树不同，二叉树严格区分左子和右子，即使只有一个子结点也要区分左右。

二叉树的树度数最大为2。

2. 性质*

关于树的一些基本念

(1)度数：一个节点的子树的个数(一个节点的子树的个数称为该节点的度数,3)

(2)树度数：树中节点的最大度数

(3)叶节点或终端节点: 度数为零的节点

(4)分支节点：度数不为零的节点(B一层)

(5)内部节点：除根节点以外的分支节点 （B，C，D）

(6)节点层次: 根节点的层次为1，根节点子树的根为第2层，以此类推

(7)树的深度或高度: 树中所有节点层次的最大值 （4）

  1. 二叉树的第k层上的结点最多个2k-1个
  2. 深度为k的二叉树最多有2k-1个结点

Sn=a1(1-qn)/(1-q)=a1(1-2k)/(1-2)=(1-2k)/-1=2k-1

  1. 在任意一颗二叉树中，树叶的数目比度数为2的结点数目多1。

N：结点的总数

N0：没有子结点的结点个数

N1：只有一个子结点的结点个数

N2：有两个子结点的结点个数

总结点 = 各节点数目之和 N = N0 + N1 + N2

总结点 = 所有子节点 + 根 N = 0 × N0 + 1 × N1 + 2 × N2 + 1

联立以上两式可得： N0 = N2 + 1

(网易)一棵二叉树有8个度为2的节点，5个度为1的节点，那么度为0的节点个数为 ( 9 )

满二叉树和完全二叉树

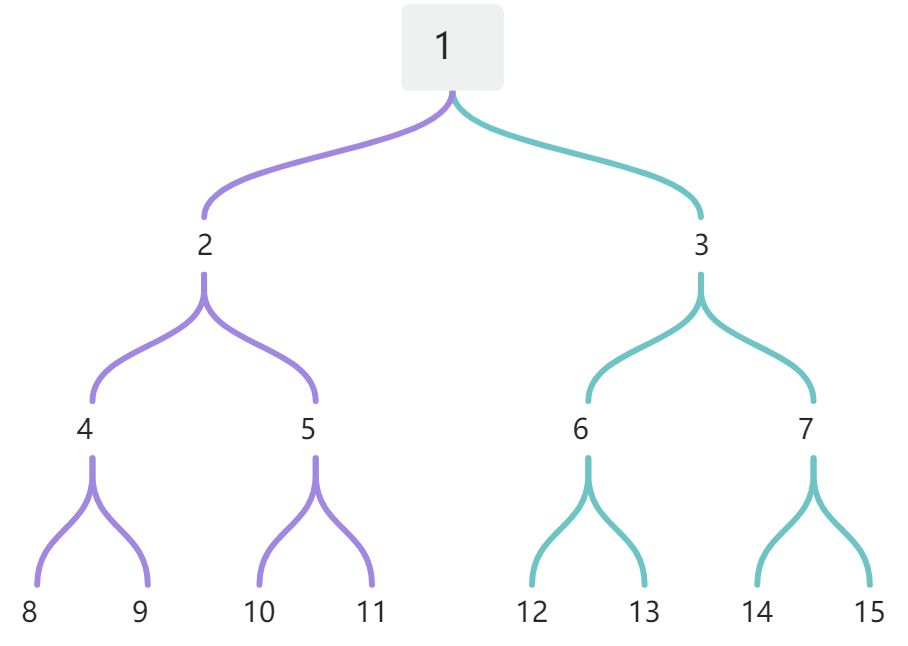
满二叉树：深度为k(k>=1)时，第k层结点个数为2k-1

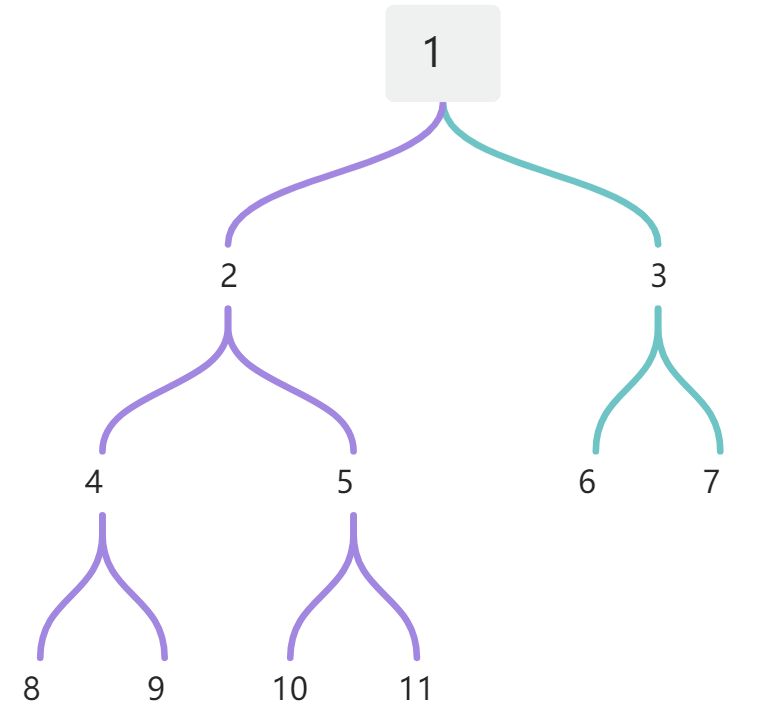
完全二叉树：只有最下面两层有度数小于2的节点，且最下面一层的结点集中在最左边的若干位置上。

3. 实现

二叉树的存储结构有两种，分为顺序存储和链式存储

3.1. 顺序存储

二叉树的顺序存储，指的是使用顺序表（数组）存储二叉树。需要注意，顺序存储只适用于完全二叉树。换句话说，只有完全二叉树才可以用顺序表存储。因此，如果我们想要顺序存储普通二叉树，就需要将其提前转换成完全二叉树。

普通二叉树转完全二叉树的方法很简单，只需给二叉树额外添加一些结点，将其"拼凑"成一个完全二叉树即可。

如图所示：

：

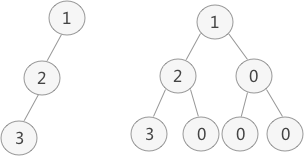
左侧是普通二叉树，右侧是转化后的完全(满)二叉树。

完全(满)二叉树的顺序存储，仅需要从根结点开始，按照层次依次将树中结点存储到数组即可。

存储图 2 所示的完全二叉树：

存储由普通二叉树转化来的完全二叉树也是如此。

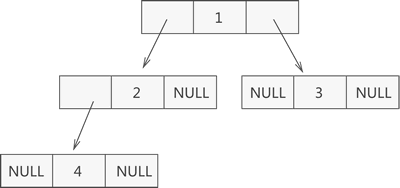
图 1 中普通二叉树在顺组中的存储状态如图：

完全二叉树中结点按照层次并从左到右依次编号（123...），若结点i有左子，则其左子的结点编号为2*i，右子编号为2*i+1。

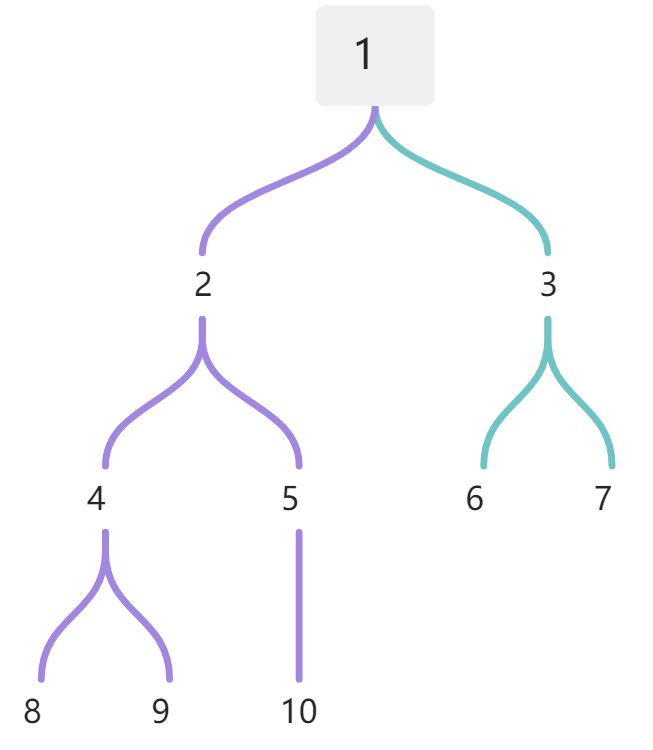
设完全二叉树的结点数为n，某结点的编号为i。

当i>1时(不是根结点时)，有父节点，其编号为i/2。

当2*i <= n时，有左子，其编号为2*i，否则没有左子，没左子一定没右子，其本身为叶节点。

当2*i+1 <= n时，有右子，其编号为2*i+1，否则就没有右子。

3.1.1. 遍历*

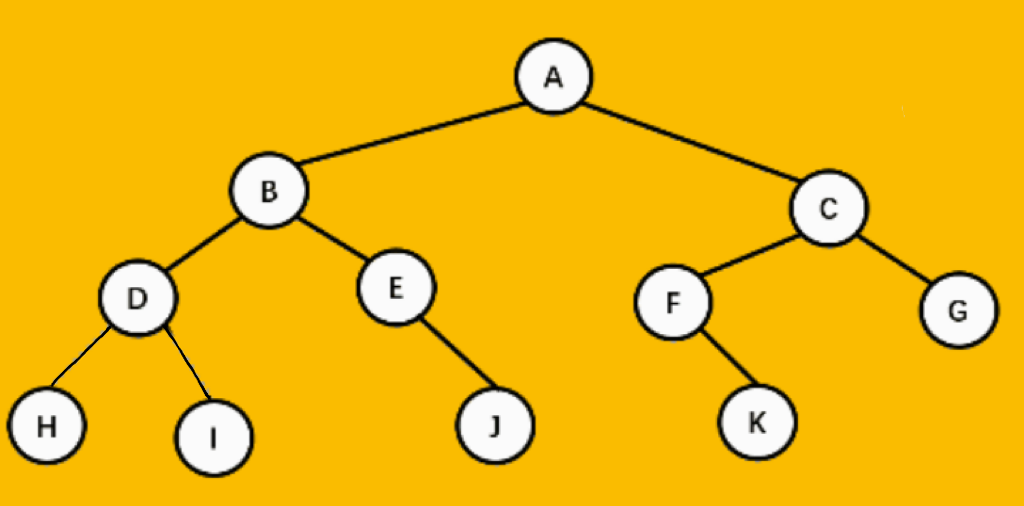
先序：根----->左----->右

A B D H I E J C F K G

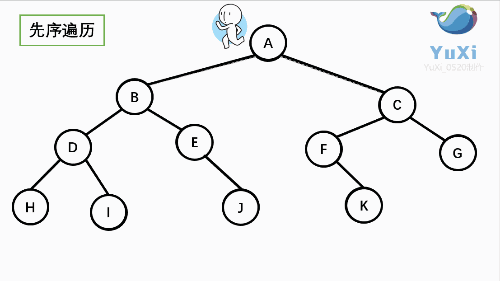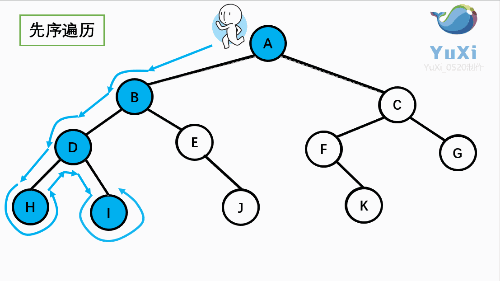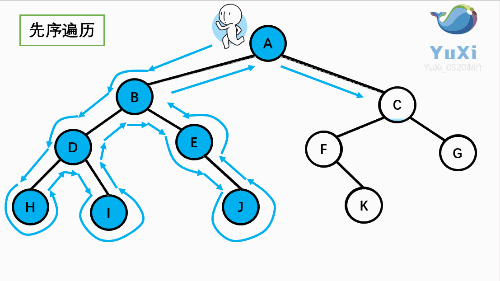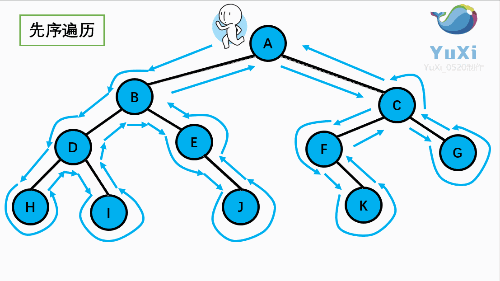
中序：左----->根----->右

H D I B E J A F K C G

后序：左----->右----->根

H I D J E B K F G C A

已知遍历结果如下，试画出对应的二叉树，写出后续：

先序：A B C E H F I J D G K 根----->左----->右

中序：A H E C I F J B D K G 左----->根----->右

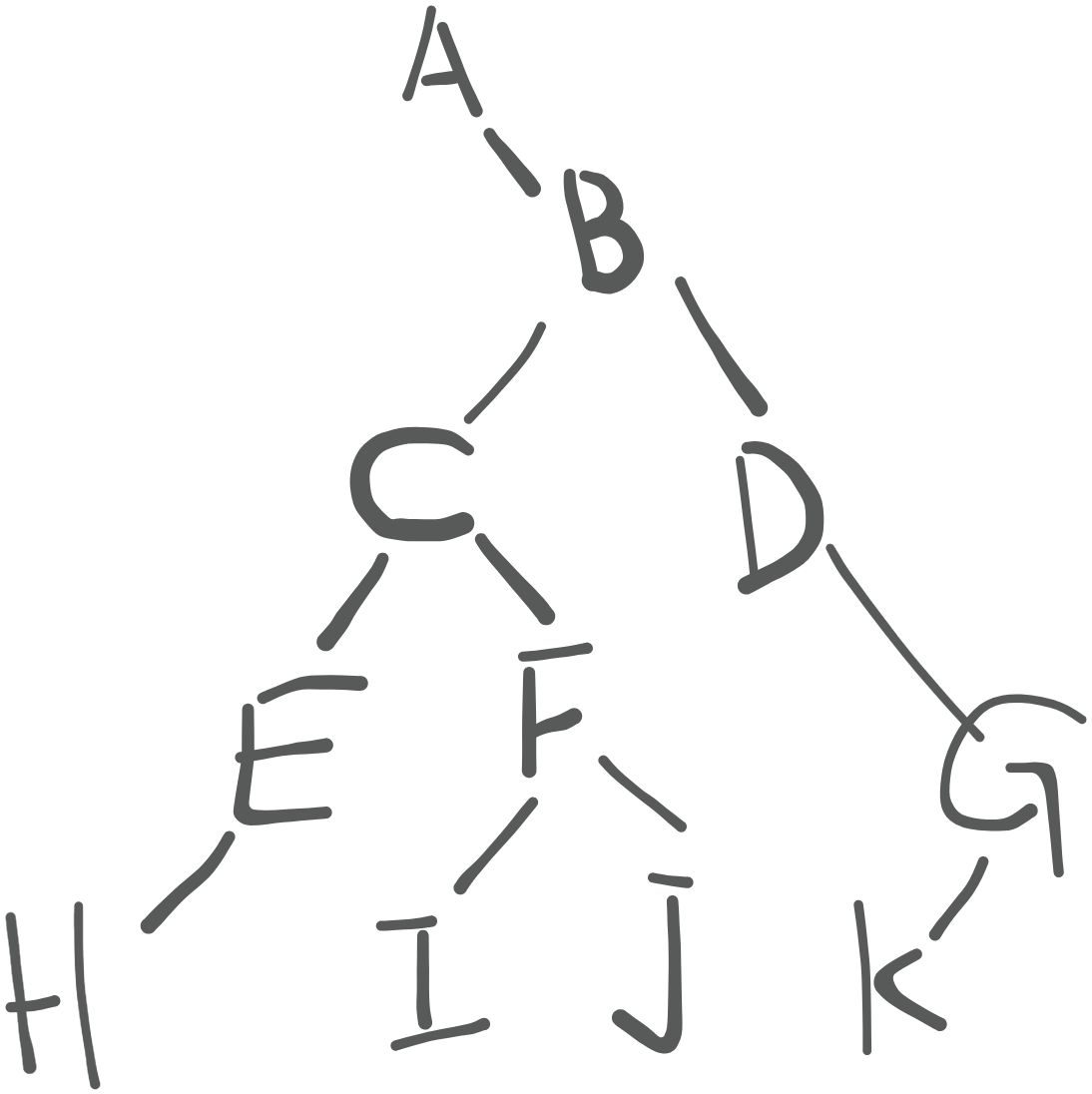
因为先序是根在最前面的，所以在先序中从前往后地取结点拿到中序中作为根，循环重复。

3.2. 链式存储

链式存储此二叉树，从根结点开始，将各个结点以及其左右子的地址使用链表进行存储。

3.2.1. 定义操作完全二叉树结构体*

结点结构体由三部分组成：

  1. 指向左子结点的指针(Lchild)
  2. 结点存储的数据（结点编号）
  3. 指向右子结点的指针(Rchild)

// 1. 定义操作二叉树的结构体
typedef char datatype_tree;
typedef struct tree_node_t
{
	datatype_tree data;//数据域
	struct tree_node_t *lchild;//左子left 
	struct tree_node_t *rchild;//右子right 
}bitree_node_t,*bitree_list_t;

3.2.2. 创建二叉树*

#include "bitree.h"

// 2. 创建二叉树
// 主函数传参 n 树中结点总数; i 结点编号(从1开始)
bitree_list_t CreateBitree(int n,int i)
{
    // 2.1 开辟空间存放结构体
	bitree_list_t r = (bitree_list_t)malloc(sizeof(bitree_node_t));

	if(NULL == r)
	{
		printf("CreateBitree malloc failed\n");
		return NULL;
	}
   // 2.2 初始化结构体成员
   // 2.3 判断有无左右子
   // 2.3.1 有左子
	r->data = i;
	if(2 * i <= n)
	{
		r->lchild = CreateBitree(n,2*i);
	}
    // 2.3.2 无左子
	else
	{
		r->lchild = NULL;
	}
   // 2.3.3 有右子
	if(2*i + 1 <= n)
	{
		r->rchild = CreateBitree(n,2*i+1);
	}
   // 2.3.4 无右子
	else
	{
		r->rchild = NULL;
	}
	return r;
}

#include "bitree.h"
int main(int argc, const char *argv[])
{
	bitree_node_t *r = CreateBitree(3,1);
	return 0;
}

3.2.3. 先序遍历*

//前序
// 3. 先序遍历二叉树
// 根——左——右
void PreOrder(bitree_list_t r)
{
	if(NULL == r)
		return;
	printf("%d ",r->data);							 // 根
 // 如果有左子，则将左子作为根将该函数的全部操作走一遍
	if(r->lchild != NULL)							 // 左
		PreOrder(r->lchild);
// 如果有右子，则将右子作为根将该函数的全部操作走一遍
	if(r->rchild != NULL)
		PreOrder(r->rchild);						 // 右
}

3.2.4. 中序遍历

// 4. 中序遍历
// 左——根——右
void InOrder(bitree_list_t r)
{
	if(NULL == r)
		return;
    // 如果有左子，则将左子作为根将该函数的全部操作走一遍
	if(r->lchild != NULL)								 // 左
		InOrder(r->lchild);
	printf("%d ",r->data);								 // 根
    // 如果有右子，则将右子作为根将该函数的全部操作走一遍
	if(r->rchild != NULL)
	InOrder(r->rchild);									 // 右
}

3.2.5. 后序遍历

// 5. 后序遍历
// 左——右——根
void PostOrder(bitree_list_t r)
{
    if(NULL == r)
		return;

    // 如果有左子，则将左子作为根将该函数的全部操作走一遍
    if (r->lchild != NULL)                           // 左
        PostOrder(r->lchild);

    // 如果有右子，则将右子作为根将该函数的全部操作走一遍
    if (r->rchild != NULL)                           // 右
        PostOrder(r->rchild);

    printf("%d\t", r->data);                         // 根
}

总结：

#include "bitree.h"
bitree_list_t CreateBitree(int n,int i)
{

	bitree_list_t r = (bitree_list_t)malloc(sizeof(bitree_node_t));
	if(NULL == r)
	{
		printf("CreateBitree malloc failed\n");
		return NULL;
	}
	r->data = i;

	if(2 * i <= n)
	{
		r->lchild = CreateBitree(n,2*i);
	}
	else
	{
		r->lchild = NULL;
	}

	if(2*i + 1 <= n)
	{
		r->rchild = CreateBitree(n,2*i+1);
	}
	else
	{
		r->rchild = NULL;
	}
	return r;
}
//前序
void PreOrder(bitree_list_t r)
{
	if(NULL == r)
		return;

	printf("%d ",r->data);
	if(r->lchild != NULL)
		PreOrder(r->lchild);
	if(r->rchild != NULL)
		PreOrder(r->rchild);
}
//中序
void InOrder(bitree_list_t r)
{
	if(NULL == r)
		return;
	if(r->lchild != NULL)
		InOrder(r->lchild);
	printf("%d ",r->data);
	if(r->rchild != NULL)
	InOrder(r->rchild);
}
//后序
void PostOrder(bitree_list_t r)
{
	if(NULL == r)
		return;
	if(r->lchild != NULL)
		PostOrder(r->lchild);
	if(r->rchild != NULL)
		PostOrder(r->rchild);
	printf("%d ",r->data);

}
#include "bitree.h"
int main(int argc, const char *argv[])
{	
	bitree_node_t *r = CreateBitree(3,1);
	PreOrder(r);	
	printf("\n");
	InOrder(r);
	printf("\n");
	PostOrder(r);
	printf("\n");
	return 0;
}
#ifndef _BITREE_H_
#define _BITREE_H_
#include <stdio.h>
#include <stdlib.h>
typedef char datatype_tree;
typedef struct tree_node_t
{
	datatype_tree data;//数据域
	struct tree_node_t *lchild;//左子left 
	struct tree_node_t *rchild;//右子right 
}bitree_node_t,*bitree_list_t;
bitree_list_t CreateBitree(int n,int i);
//前序
void PreOrder(bitree_list_t r);
//中序
void InOrder(bitree_list_t r);
//后序
void PostOrder(bitree_list_t r);
//层次
void unOrder(bitree_list_t r);
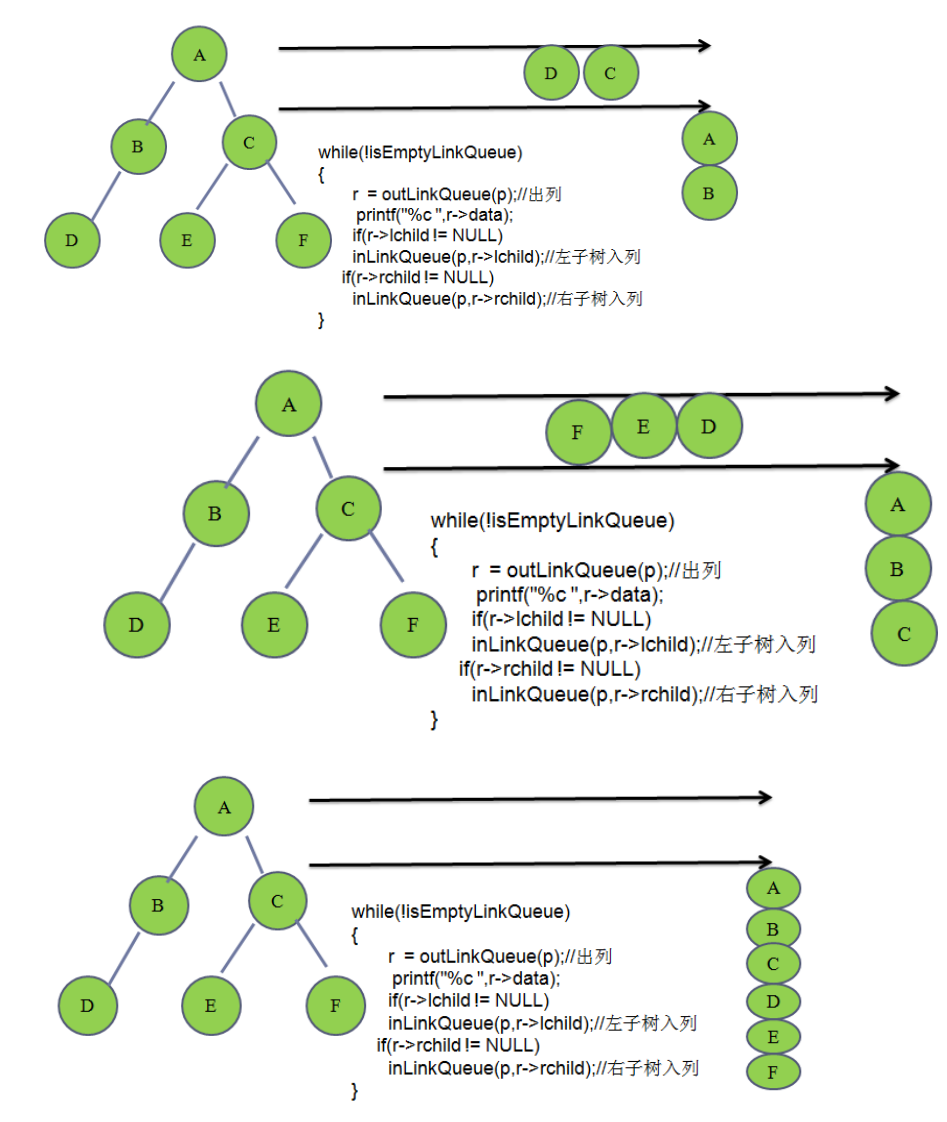
#endif

3.2.6. 层序遍历

队列的思想

不需要敲代码，看懂就行

示意图

#ifndef _BITREE_H_
#define _BITREE_H_
typedef char datatype_tree;
typedef struct tree_node_t
{
	datatype_tree data;//数据域 
	struct tree_node_t *lchild;//左子指针
	struct tree_node_t *rchild;//右子指针
}bitree_t;
//前序遍历
void preOrder(bitree_t *r);//r二叉树根节点的指针
//中序遍历
void inOrder(bitree_t * r);
//后序遍历
void postOrder(bitree_t *r);
//遍历二叉树 
//s 代表的是打印提示, void (*p)(bitree_t *)函数指针  r遍历的树
void showBitree(char *s,void (*p)(bitree_t *),bitree_t *r);
//创建二叉树,用递归函数创建
bitree_t *createBitree();
//层次遍历
void unOrder(bitree_t *r);
#endif
#ifndef _LINKQUEUE_H_
#define _LINKQUEUE_H_

#include "bitree.h"

//将 bitree_t * 改名 为datatype_linkqueue 
typedef bitree_t * datatype_linkqueue;//把队列的数据域变成指向树节点的指针
typedef struct node
{
	datatype_linkqueue data;//数据域
	struct node *next;//指针域
}linkqueue_node_t,*linkqueue_list_t;

//linkqueue_list_t p === linkqueue_node_t *
typedef struct//将队列头指针和尾指针封装到一个结构体里
{
	linkqueue_list_t front;//相当于队列的头指针
	linkqueue_list_t rear;//相当于队列的尾指针
	//有了链表的头指针和尾指针，那么我们就可以操作这个链表
}linkqueue_t;

//1.创建一个空的队列
linkqueue_t *createEmptyLinkQueue();
//2.入列 data代表入列的数据
int inLinkQueue(linkqueue_t *p,datatype_linkqueue data);
//3.出列 
datatype_linkqueue outLinkQueue(linkqueue_t *p);
//4.判断队列是否为空
int isEmptyLinkQueue(linkqueue_t *p);
//5.求队列长度的函数
int lengthLinkQueue(linkqueue_t *p);
//6.清空队列
void clearLinkQueue(linkqueue_t *p);
#endif
#include "bitree.h"
#include "linkqueue.h"
#include <stdio.h>
#include <stdlib.h>
//前序遍历
void preOrder(bitree_t *r)//r二叉树根节点的指针
{
	if(r == NULL)//递归函数的结束条件
		return;
	printf("%c ",r->data);//根
	preOrder(r->lchild);//左
	preOrder(r->rchild);//右
}
//中序遍历
void inOrder(bitree_t * r)
{
	if(r == NULL)//递归的结束条件
		return;
	inOrder(r->lchild);//左
	printf("%c ",r->data);//根
	inOrder(r->rchild);//右
}
//后序遍历
void postOrder(bitree_t *r)
{
	if(r == NULL)//递归函数的结束条件
		return;
	postOrder(r->lchild);//左
	postOrder(r->rchild);//右
	printf("%c ",r->data);//根
}
//遍历二叉树 
//s 代表的是打印提示, void (*p)(bitree_t *)函数指针  r遍历的树
void showBitree(char *s,void (*p)(bitree_t *),bitree_t *r)
{
	printf("%s",s);
	p(r);
	printf("\n");
}
//创建二叉树,用递归函数创建
bitree_t *createBitree()
{//root 
//	ABD###CE##F##
	bitree_t *r = NULL;//用来保存二叉树的根节点
	char ch;
	scanf("%c",&ch);
	if(ch == '#')//输入是'#'，代表没有左子或右子
		return NULL;
	r = (bitree_t *)malloc(sizeof(bitree_t));
	if(NULL == r)
	{
		perror("r malloc failed");
		return NULL;
	}
	r->data = ch;
	r->lchild = createBitree();
	r->rchild = createBitree();
	return r;
}

//层次遍历
void unOrder(bitree_t *r)
{
	//1.创建一个队列,队列的数据域变成指向树节点的指针
	linkqueue_t *p = createEmptyLinkQueue();
	if(r != NULL)
		inLinkQueue(p,r);
	//2.循环打印
	while(!isEmptyLinkQueue(p))
	{
		r = outLinkQueue(p);
		printf("%c ",r->data);
		if(r->lchild != NULL)//只要左子不为空，就入列，之后出列的时候打印
			inLinkQueue(p,r->lchild);
		if(r->rchild != NULL)//只要右子不为空，就入列，之后出列的时候打印
			inLinkQueue(p,r->rchild);
	}
}
#include "linkqueue.h"
#include <stdio.h>
#include <stdlib.h>

//1.创建一个空的队列
linkqueue_t *createEmptyLinkQueue()
{
	linkqueue_t *p = (linkqueue_t *)malloc(sizeof(linkqueue_t));
	if(NULL == p)
	{
		perror("createEmptyLinkQueue p malloc failed");
		return NULL;
	}//申请空间就是为了装东西
	//申请链表的头节点空间，让rear和front都指向头结点
	p->front = p->rear = (linkqueue_list_t)malloc(sizeof(linkqueue_node_t));
	if(NULL == p->rear)
	{
		perror("p->rear malloc failed");
		return NULL;
	}
	p->rear->next = NULL;//或者用p->front->next = NULL;因为p->rear 和 p->front 指向同一个位置即头节点
	return p;
}
//2.入列 data代表入列的数据
int inLinkQueue(linkqueue_t *p,datatype_linkqueue data)
{
	//1.创建一个新的节点，用来保存即将插入的数据
	linkqueue_list_t pnew = (linkqueue_list_t)malloc(sizeof(linkqueue_node_t));
	if(NULL == pnew)
	{
		perror("inLinkQueue pnew malloc failed");
		return -1;
	}
	//2.将入列的数据放入到新的节点中
	pnew->data = data;
	pnew->next = NULL;
	//3.将新节点链链接到链表的尾巴
	p->rear->next = pnew;//新节点链接到链表的尾
	p->rear = pnew;//rear移动，因为rear永远指向当前链表的尾
	return 0;
}
//3.出列 
datatype_linkqueue outLinkQueue(linkqueue_t *p)
{
	linkqueue_list_t pdel = NULL;//指向被删除的节点
	//1.容错判断
	if(isEmptyLinkQueue(p))
	{
		printf("isEmptyLinkQueue !!\n");
		return NULL;
	}
	//2.出列数据
	//(1)定义pdel指向即将被删除的节点就是front指向的节点，出列每次删除的都是front指向的那个节点
	pdel = p->front;
	//(2)将front向后移动一个位置
	p->front = p->front->next;
	//(3)释放被删除节点
	free(pdel);
	pdel = NULL;
	//(4)将数据出列
	return p->front->data;
}
//4.判断队列是否为空
int isEmptyLinkQueue(linkqueue_t *p)
{
	return p->front == p->rear;
}
//5.求队列长度的函数
int lengthLinkQueue(linkqueue_t *p)
{
	int len = 0;
	linkqueue_list_t h = p->front;//将链表的头指针保存的地址给h,如果直接用front，求长度之后会找不到链表的头，用h的移动代替front的移动
	//求长度，相当于遍历有头的单向链表
	while(h->next != NULL)
	{
		h = h->next;
		len++;
	}
	return len;
}
//6.清空队列
void clearLinkQueue(linkqueue_t *p)
{
	while(!isEmptyLinkQueue(p))//只要不为空，就出列
		outLinkQueue(p);
}
#include "bitree.h"
#include <stdio.h>
#include <stdlib.h>

int main(int argc, const char *argv[])
{
	bitree_t *r = createBitree();
	showBitree("前序:",preOrder,r);
	showBitree("中序:",inOrder,r);
	showBitree("后序:",postOrder,r);
	showBitree("层次:",unOrder,r);
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1894302.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

cloudreve 设置开机服务

cloudreve 设置开机服务

创建一个Systemd服务文件&#xff1a; 打开终端并创建一个新的服务文件&#xff1a; sudo nano /etc/systemd/system/cloudreve.service 在服务文件中添加以下内容&#xff1a; 根据你的设置调整路径和参数&#xff0c;然后将以下配置粘贴到文件中&#xff1a; [Unit] Descri…
阅读更多...
二分查找及其变种

二分查找及其变种

一、概念 二分查找算法&#xff08;Binary Search Algorithm&#xff09;是一种在有序数组中查找特定元素的高效搜索方法。 其基本思想是将目标值与数组中间的元素进行比较&#xff0c;如果目标值等于中间元素&#xff0c;则查找成功&#xff1b;如果目标值小于中间元素&…
阅读更多...
指标和量化交易那些事儿

指标和量化交易那些事儿

最近很多朋友都在给我说&#xff0c;我要盘中打板的指标&#xff0c;我要盘中自动交易。今天我们来梳理下关于指标和量化交易这些事儿&#xff01; 第一&#xff1a;什么是指标&#xff1f;股票指标是属于统计学的范畴&#xff0c;依据一定的数理统计方法&#xff0c;运用一些…
阅读更多...
2024 年 亚太赛 APMCM （C题）中文赛道国际大学生数学建模挑战赛 | 量子计算的物流配送 | 数学建模完整代码+建模过程全解全析

2024 年 亚太赛 APMCM （C题）中文赛道国际大学生数学建模挑战赛 | 量子计算的物流配送 | 数学建模完整代码+建模过程全解全析

当大家面临着复杂的数学建模问题时&#xff0c;你是否曾经感到茫然无措&#xff1f;作为2022年美国大学生数学建模比赛的O奖得主&#xff0c;我为大家提供了一套优秀的解题思路&#xff0c;让你轻松应对各种难题&#xff01; 完整内容可以在文章末尾领取&#xff01; 该段文字…
阅读更多...
PyTorch - 神经网络基础

PyTorch - 神经网络基础

神经网络的主要原理包括一组基本元素&#xff0c;即人工神经元或感知器。它包括几个基本输入&#xff0c;例如 x1、x2… xn &#xff0c;如果总和大于激活电位&#xff0c;则会产生二进制输出。 样本神经元的示意图如下所述。 产生的输出可以被认为是具有激活电位或偏差的加权…
阅读更多...
班迪录屏（Bandicam）7.0下载以及安装教程

班迪录屏（Bandicam）7.0下载以及安装教程

最近有小伙伴私信我&#xff0c;问我有没有好用的录屏工具&#xff0c;今天给大家分享一个我一直在使用的录屏工具&#xff0c;也是解锁了V1P版本&#xff0c;绿色版打开就可以使用~ Bandicam录屏&#xff08;PC&#xff09; Bandicam录屏是一款专为捕捉屏幕精彩瞬间而设计的…
阅读更多...
go——Swagger使用

go——Swagger使用

一. 为什么后端需要配置Swagger 在前后端分离的项目中&#xff0c;后端配置swagger可以很好的帮助前端人员了解后端接口参数和数据传输。 Swagger是一个用于设计&#xff0c;构建和文档化API的开源框架。在Go语言中&#xff0c;Swagger可以帮助后端开发人员快速创建和定义RESTf…
阅读更多...
电传动无杆飞机牵引车交付用户

电传动无杆飞机牵引车交付用户

自2019年起&#xff0c;我们计划做电传动控制&#xff0c;先后做了电传动水泥搅拌罐车罐体控制&#xff08;国内首创&#xff09;&#xff0c;初步理解了电机控制的特点。 20-21年接着做了10t飞机牵引车控制&#xff0c;还是电液控制联合的&#xff0c;把越野叉车的行驶控制方…
阅读更多...
Python学习之小游戏--坦克大作战

Python学习之小游戏--坦克大作战

今天跟视频学习了Python实现坦克大作战小游戏&#xff0c;挺有意思的&#xff0c;一起来玩吧~ 按空格发射子弹&#xff0c;上下左右键实现移动&#xff0c;ESC键无限复活。 import pygame,time,random from pygame.sprite import Sprite SCREEN_WIDTH800 SCREEN_HEIGHT500 BG…
阅读更多...
玩机进阶教程----MTK芯片杂牌机 小品牌机型解除bl锁以及root的操作步骤解析

玩机进阶教程----MTK芯片杂牌机 小品牌机型解除bl锁以及root的操作步骤解析

在玩机过程中会遇到很多小品牌机型或者杂牌机类的。大多都使用mtk芯片。而且基本很少有官方线刷包。在这些机型中玩机首先我们要想办法导出系统来制作线刷包。以免后续解锁bl或者root出现未知故障可以恢复原系统。 那么对于这些机型该如何进行备份固件和root呢。通过博文可以初…
阅读更多...
图书借阅小程序论文（设计）开题报告

图书借阅小程序论文（设计）开题报告

一、课题的背景和意义 近些年来&#xff0c;随着移动互联网巅峰时期的来临&#xff0c;互联网产业逐渐趋于“小、轻、微”的方向发展&#xff0c;符合轻应用时代特点的各类技术受到了不同领域的广泛关注。在诸多产品中&#xff0c;被誉为“运行着程序的网站”之名的微信小程序…
阅读更多...
开始尝试从0写一个项目--前端（一）

开始尝试从0写一个项目--前端（一）

基础项目构建 创建VUE初始工程 确保自己下载了node.js和npm node -v //查看node.js的版本 npm -v //查看npm的版本 npm i vue/cli -g //安装VUE CLI 创建 以管理员身份运行 输入&#xff1a;vue ui 就会进入 点击创建 自定义项目名字&#xff0c;选择npm管理 结…
阅读更多...
什么是多态（Polymorphism）

什么是多态（Polymorphism）

什么是多态&#xff08;Polymorphism&#xff09; 1、多态的基本概念2、多态的实现方式2.1 方法重载&#xff08;Overloading&#xff09;2.2 方法重写&#xff08;Overriding&#xff09;2.3 接口和抽象类 3、为什么要使用多态&#xff1f;4、结论 &#x1f496;The Begin&…
阅读更多...
启明智显Model3A芯片方案7寸高清触摸屏ZX7D00CM21S：开箱、设置与实操全攻略指南

启明智显Model3A芯片方案7寸高清触摸屏ZX7D00CM21S：开箱、设置与实操全攻略指南

一、背景 本指南将详细介绍启明智显的Model3A芯片方案下的7寸高清触摸屏ZX7D00CM21S的开箱步骤、基础设置以及实操应用。无论您是电子爱好者、开发者还是工程师&#xff0c;这份指南都能助您快速上手并充分利用这款触摸屏的各项功能。 二、硬件介绍 ZX7D00CM21S 7寸高清触摸屏是…
阅读更多...
500mA、低压差、低噪声、超快、无需旁路电容的CMOS LDO稳压器RT9013

500mA、低压差、低噪声、超快、无需旁路电容的CMOS LDO稳压器RT9013

一般描述 RT9013 SOT23-5封装的外观和丝印 RT9013 是一款高性能的 500mA LDO 稳压器&#xff0c;具有极高的 PSRR 和超低压差。非常适合具有苛刻性能和空间要求的便携式射频和无线应用。 RT9013的静态电流低至25μA&#xff0c;进一步延长了电池的使用寿命。RT9013 也适用于低…
阅读更多...
kafka的工作原理与常见问题

kafka的工作原理与常见问题

定义 kafka是一个分布式的基于发布/订阅模式的消息队列&#xff08;message queue&#xff09;&#xff0c;主要应用于大数据的实时处理领域 消息队列工作原理 kafka的组成结构 kafka的基础架构主要有broker、生产者、消费者组构成&#xff0c;还包括zookeeper. 生产者负责发送…
阅读更多...
【Android源码】Gerrit安装

【Android源码】Gerrit安装

前言 如果你打开 https://android.googlesource.com/platform/manifest&#xff0c;就会发现&#xff0c;google官方管理Android源码&#xff0c;使用的是Gerrit。Android系统源码是非常大的&#xff0c;用Git肯定是不适合。对于大型项目&#xff0c;得用Gerrit&#xff0c;今…
阅读更多...
小龙虾优化24种机器学习多输入单输出回归|时序预测模型

小龙虾优化24种机器学习多输入单输出回归|时序预测模型

小龙虾优化24种机器学习多输入单输出回归|时序预测模型 文章目录 小龙虾优化24种机器学习多输入单输出回归|时序预测模型前言一、小龙虾优化基本原理二、优化机器学习模型1.COA-CNN-BiGRU-Attention回归模型2.基于小龙虾优化支持向量机的数据回归预测Matlab程序COA-SVM 多特征输…
阅读更多...
Web应用防火墙用在哪些场景？

Web应用防火墙用在哪些场景？

WAF是Web Application Firewall的缩写&#xff0c;翻译为“Web应用防火墙”是一种网络安全设备或服务&#xff0c;用于保护Web应用程序免受各种网络攻击和漏洞的影响。 WAF特别设计用于识别和阻止特定于Web应用程序的攻击&#xff0c;例如SQL注入、跨站脚本(XSS)、跨站请求伪造…
阅读更多...
014-GeoGebra基础篇-快速解决滑动条的角度无法输入问题

014-GeoGebra基础篇-快速解决滑动条的角度无法输入问题

有客户反馈&#xff0c;他的Geogebra一直有个bug&#xff0c;那就是输入角度最大值时总不按照他设定的展示&#xff0c;快被气炸了~ 目录 一、问题复现&#xff08;1&#xff09;插入一个滑动条&#xff08;2&#xff09;选择Angle&#xff08;3&#xff09;输入90&#xff0c;…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023