一、概念

二分查找算法（Binary Search Algorithm）是一种在有序数组中查找特定元素的高效搜索方法。

其基本思想是将目标值与数组中间的元素进行比较，如果目标值等于中间元素，则查找成功；如果目标值小于中间元素，则在数组左半部分继续查找；如果目标值大于中间元素，则在数组右半部分继续查找。这个过程将不断重复，直到找到目标值或搜索范围为空为止。

二、实现步骤

2.1 初始化: 确定搜索范围的左右边界，通常用两个指针表示，一个指向数组的起始位置（left，索引0），另一个指向数组的结束位置（right，数组长度减1）。

2.2 循环条件: 当左指针小于等于右指针时，继续查找。

2.3 计算中间索引: 计算当前搜索范围的中间位置 mid，通常使用 (left + right) / 2 来避免整数溢出。

口诀：奇数二分取中间 偶数二分取中间靠左；

2.4 比较中间元素: 比较 array[mid] 与目标值 target：

• 如果 array[mid] 等于 target，则查找成功，返回 mid。
• 如果 array[mid] 大于 target，则在左半部分继续查找，更新右指针 right = mid - 1。
• 如果 array[mid] 小于 target，则在右半部分继续查找，更新左指针 left = mid + 1。

2.5 结束循环: 如果左指针大于右指针，表示搜索范围为空，目标值不在数组中，返回一个表示未找到的值，如 -1。

三、代码实现

public class BinarySearch {
    public int binarySearch(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        
        while (left <= right) {
            int mid = left + (right - left) / 2; // 防止溢出
            if (nums[mid] == target) {
                return mid; // 找到目标值，返回索引
            } else if (nums[mid] < target) {
                left = mid + 1; // 在右半部分查找
            } else {
                right = mid - 1; // 在左半部分查找
            }
        }
        
        return -1; // 未找到目标值，返回-1
    }
}

注意事项：

 1. 如果left 和 right比较大的话，两者之和就有可能会溢出。改进的方法是将 mid 的计算方式写成 left +(right-left )/2。更进一步，如果要将性能优化到极致的话，我们可以将这里的除以 2 操作转化成位运算 left +((right-left )>>1)。因为相比除法运算来说，计算机处理位运算要快得多。

2. while  (left < = right)，注意括号内为 left <= right ，而不是 left < right ，如果我们设置条件为 left  <  right 则当我们执行到最后一步时，则我们的 left 和 right 重叠时，则会跳出循环，返回 -1，区间内不存在该元素，但是不是这样的，我们的 left 和 right 此时指向的就是我们的目标元素 ，但是此时 left = right 跳出循环

3. left = mid + 1,right = mid - 1 而不是 left = mid 和 right = mid。当我们的target 元素为 16 时，然后我们此时 left = 7 ，right = 8，mid = left + (right - left) = 7 + (8-7) = 7，那如果设置 left = mid 的话，则会进入死循环，mid  值一直为7 。

四、算法变种

4.1 

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

示例 1：
输入：nums = [5,7,7,8,8,10], target = 8 输出：[3,4]

示例 2：
输入：nums = [5,7,7,8,8,10], target = 6 输出：[-1,-1]

示例 3：
输入：nums = [], target = 0 输出：[-1,-1]

从最原始的二分查找代码中分析， nums[mid] == target 时则返回，nums[mid] < target 时则移动左指针，在右区间进行查找， nums[mid]  >  target 时则移动右指针，在左区间内进行查找。

那么我们思考一下，如果此时我们的 nums[mid] = target ，但是我们不能确定 mid 是否为该目标数的左边界，所以此时我们不可以返回下标。

 

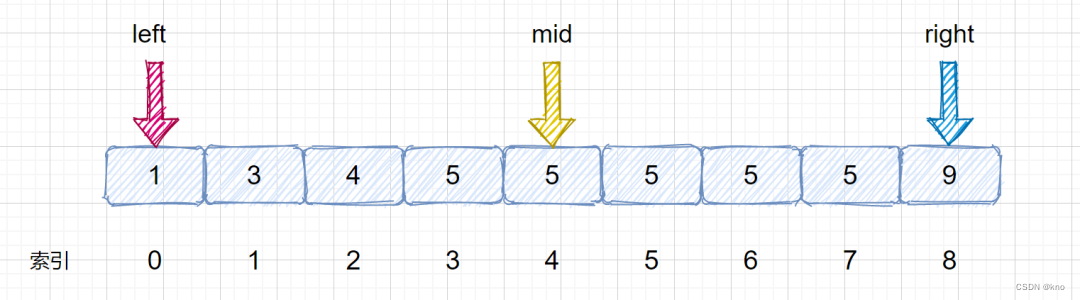
此时 mid = 4 ，nums[mid] = 5，但是此时的 mid 指向的并不是第一个 5，所以我们需要继续查找 ，因为我们要找的是数的下边界，所以我们需要在 mid 的值的左区间继续寻找 5 ，那应该怎么做呢？

我们只需在target <= nums[mid] 时，让 right = mid - 1即可，这样我们就可以继续在 mid 的左区间继续找 5 。

解决方案：

将小于和等于合并在一起处理，当 target <= nums[mid] 时，我们都移动右指针，也就是 right = mid -1，还有一个需要注意的就是，我们计算下边界时最后的返回值为 left ，当上图结束循环时，left = 3，right = 2，返回 left 刚好时我们的下边界。

计算上边界时算是和计算上边界时条件相反，

计算下边界时，当  target <= nums[mid]  时，right = mid -1；target > nums[mid] 时，left = mid + 1；

计算上边界时，当  target < nums[mid] 时，right = mid -1; target >= nums[mid] 时 left = mid + 1;刚好和计算下边界时条件相反，返回right。

public class Solution {
   
    public static int[] searchRange(int[] nums,int target){
        int upper = upperBound(nums, target);
        int low = lowerBound(nums, target);
        //不存在情况
        if (upper < low){
            return new int[]{-1,-1};
        }
        return new int[]{low,upper};
    }

    //计算下边界
    static int lowerBound(int[] nums,int target){
        int left = 0, right = nums.length - 1;
        while (left <= right){
            //计算mid
            int mid = left + ((right - left) >> 1);
            if (target <= nums[mid]){
                //当目标值小于等于nums[mid]时，继续在左区间检索，找到第一个数
                right = mid -1;
            }else if (target > nums[mid]){
                //目标值大于nums[mid]时，则在右区间继续检索，找到第一个等于目标值的数
                left = mid + 1;
            }
        }
        return left;
    }

    //计算上边界
    static int upperBound(int[] nums,int target){
        int left = 0,right = nums.length - 1;
        while (left <= right){
            int mid = left + ((right - left) >> 1);
            if (target >= nums[mid]){
                left = mid + 1;
            }else if (target < nums[mid]){
                right = mid - 1;
            }
        }
        return right;
    }
}