一.向下调整建堆
1.二叉树层数与总节点个数关系
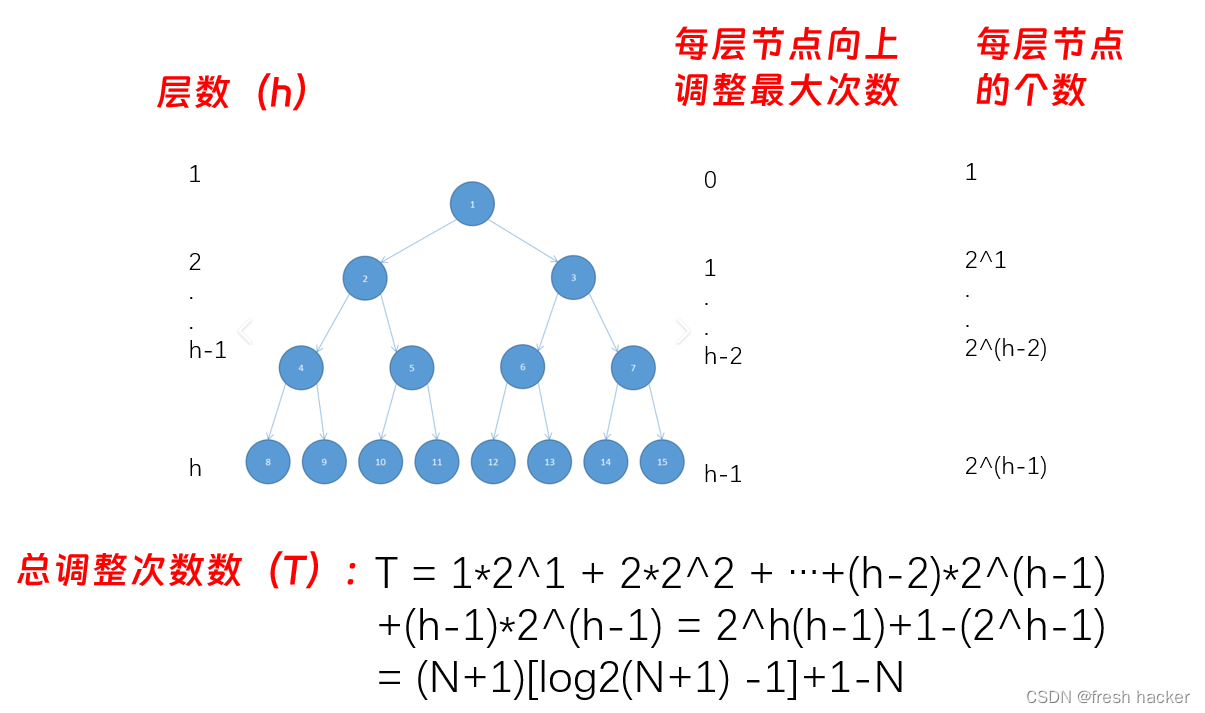
层数一定时,在二叉树节点个数最大的情况下,二叉树为满二叉树,如下图所示,可以清晰地看到在满二叉树中第h层有2^(h-1)个节点,总节点N就等于一个等比数列的求和,运用等比数列求和公式可以得到:N = 2^h - 1
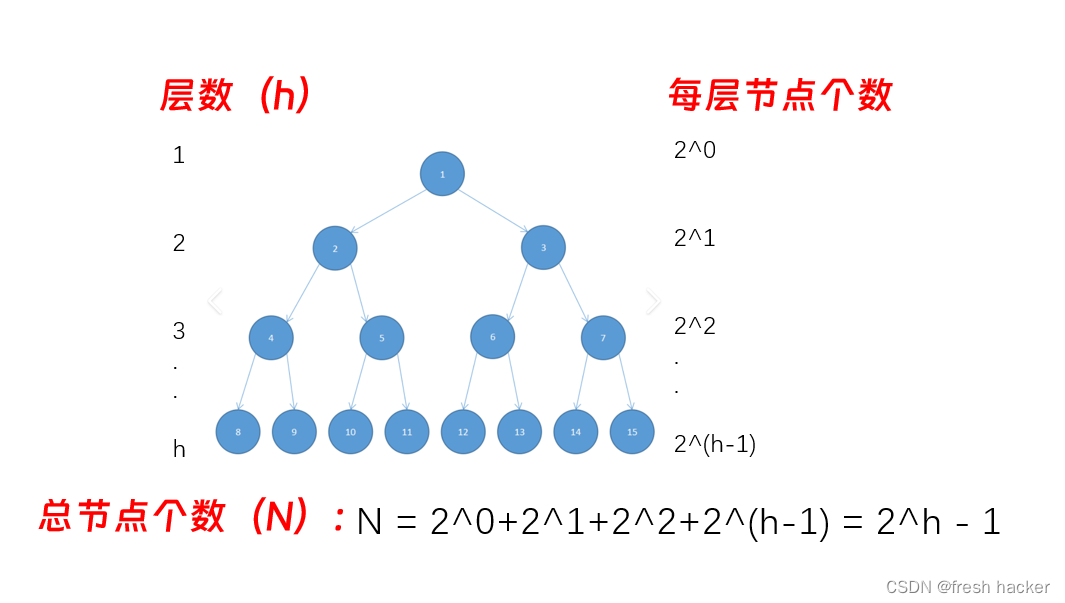
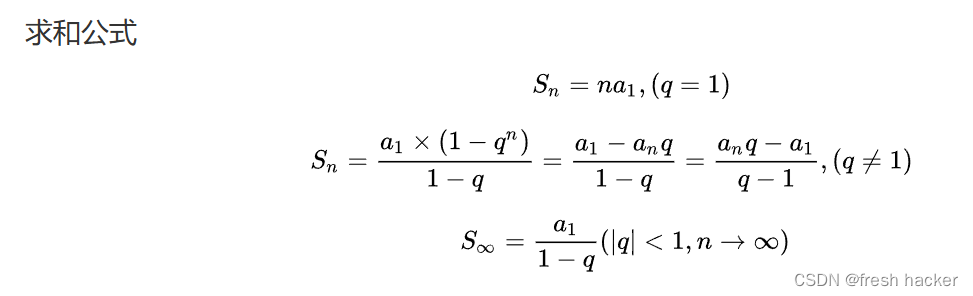
当然还得考虑节点最少的情况,此时第h-1层仍是满节点的,第h层只有一个节点,此时,可以使用上述公式得到h-1层满二叉树总节点为2^(h-1) - 1个,再加上第h层的1个节点,总节点N = 2^(h-1)个
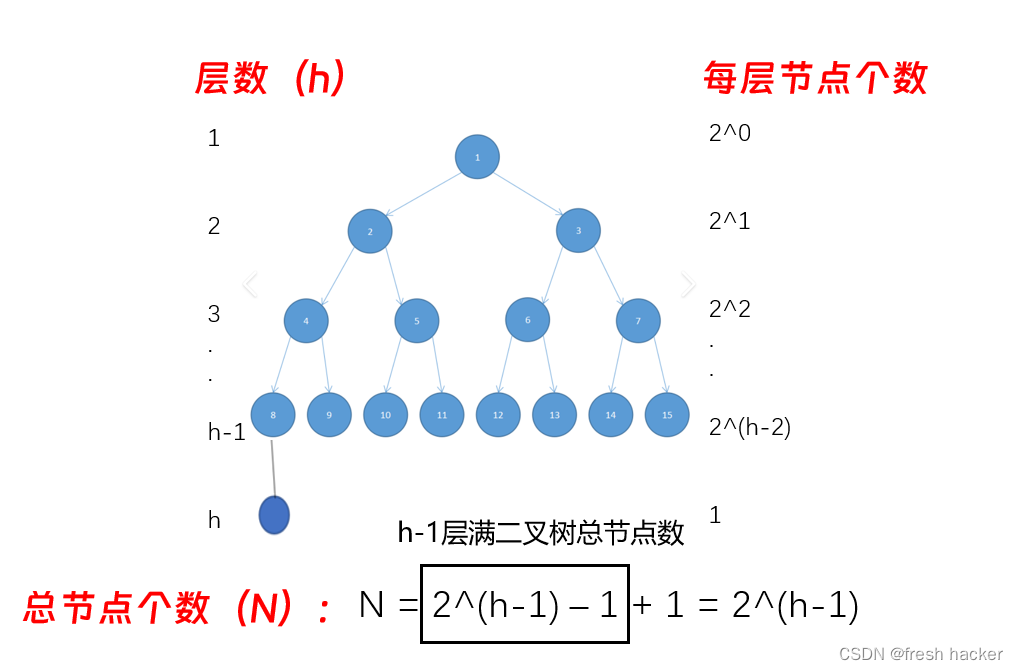
2.单次向下调整的时间复杂度
 由最终结论可以看出,无论是节点最多还是最少的情况,h与N关系的量级都是logN,同时h可以表示单次向下调整的最大次数-1,那么单次向下调整的时间复杂度就是logN
由最终结论可以看出,无论是节点最多还是最少的情况,h与N关系的量级都是logN,同时h可以表示单次向下调整的最大次数-1,那么单次向下调整的时间复杂度就是logN
3.向下调整总次数
在这篇文章里:【数据结构】二叉树-堆_数据结构树可以有三个子树吗-CSDN博客介绍了向下调整算法的思想,就是从最后一个节点的父节点开始依次进行向下调整,直到最后从下标为0的根节点向下调整完毕,那么这个总的调整次数是多少,这同样是能够计算出的。
从最后一个节点的父节点开始向下调整,即从h-1层开始,该层的每个节点向下调整最多调整1次,第h-2层最多调整2次,如此直到第1层需要h-1次,那么每层对应的最多调整次数乘上每层的节点数,就是最多情况下需要的调整次数了。该数列是等差比数列,使用错位相减法可以得出结论,过程如下图所示:
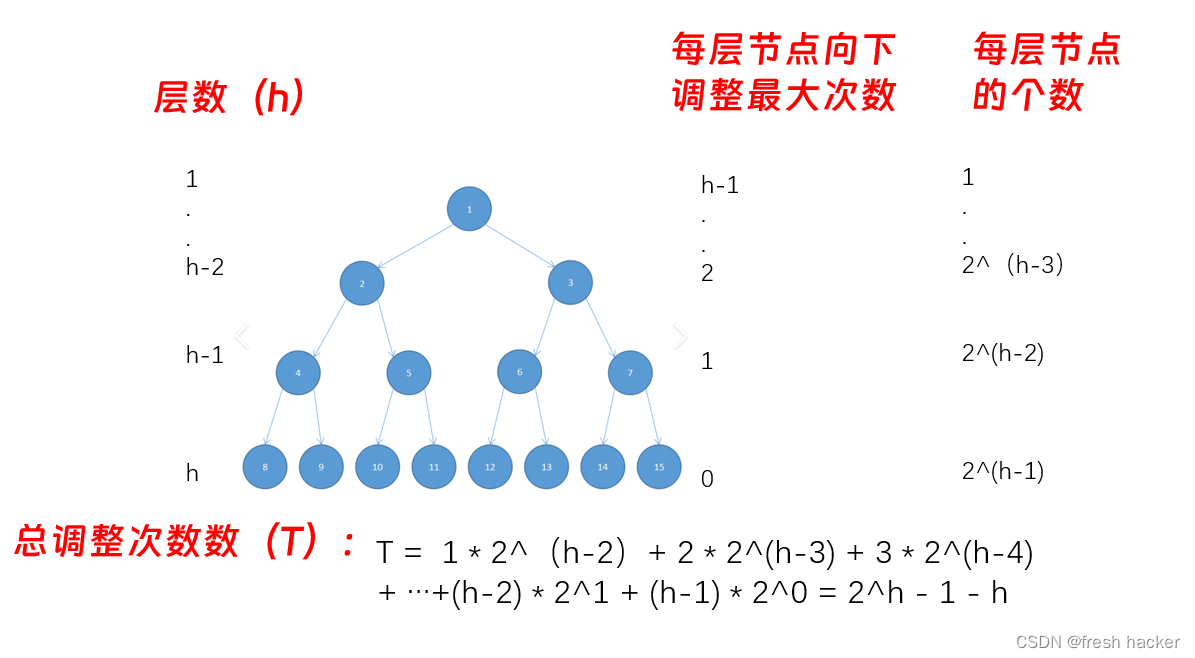
注:最后一层不需要调整(调整次数为0),故不需要考虑是否是满二叉树的情况,该式子都成立
4.时间复杂度O(N)
注意,时间复杂度不能仅是简单的N个数据乘以单次向下调整的时间复杂度为(N*logN),这是错误的,必须列出具体的关系式再来看。
时间复杂度看的是最坏情况,此时每个节点的调整次数都是最大。时间复杂度是数据个数(N)和执行次数(T)之间的关系,那么此时用已知的两个结论(二叉树层数与总结点关系的结论),用层数(h)为桥梁建立起T与N的关系为如下,时间复杂度舍小取大,N层级大于logN,取N,则时间复杂度为O(N)
二.向上调整建堆O(N*logN)
明白了向下调整建堆,那么向上调整建堆就很容易了,与向下调整同理,不过得出的结果是向上调整算法的时间复杂度为O(N*logN),远远大于向下调整的O(N),其实这很容易看出,向上调整时越往下调整次数越多,同时越往下每层的节点也越多,多的节点乘以多的调整次数,很显然比不过向下调整的 多节点乘以少的调整次数。
下图中使用的是满二叉树时N对应h的结论,其实不管使用哪个N对应h的结论都一样,因为其量级就为logN,最后的结果也是不变的。