一 滑动窗口设计知识点
滑动窗口是什么?
滑动窗口是一种想象出来的数据结构: 滑动窗口有左边界L和有边界R 在数组或者字符串或者一个序列上,记为S,窗口就是S[L..R]这一部分 L往右滑意味着一个样本出了窗口,R往右滑意味着一个样本进了窗口 L和R都只能往右滑
滑动内最大值和最小值的更新结构
窗口不管L还是R滑动之后,都会让窗口呈现新状况, 如何能够更快的得到窗口当前状况下的最大值和最小值? 最好平均下来复杂度能做到O(1) 利用单调双端队列!
1.1 概念
任何时候l和r都可以往右动,遵循的原则L不能大于R,R不能大于数组的右侧边界 L和R不能回退

二 求每次形成窗口的最大值
可以在每次形成窗口的时候遍历窗口的数据求最大值
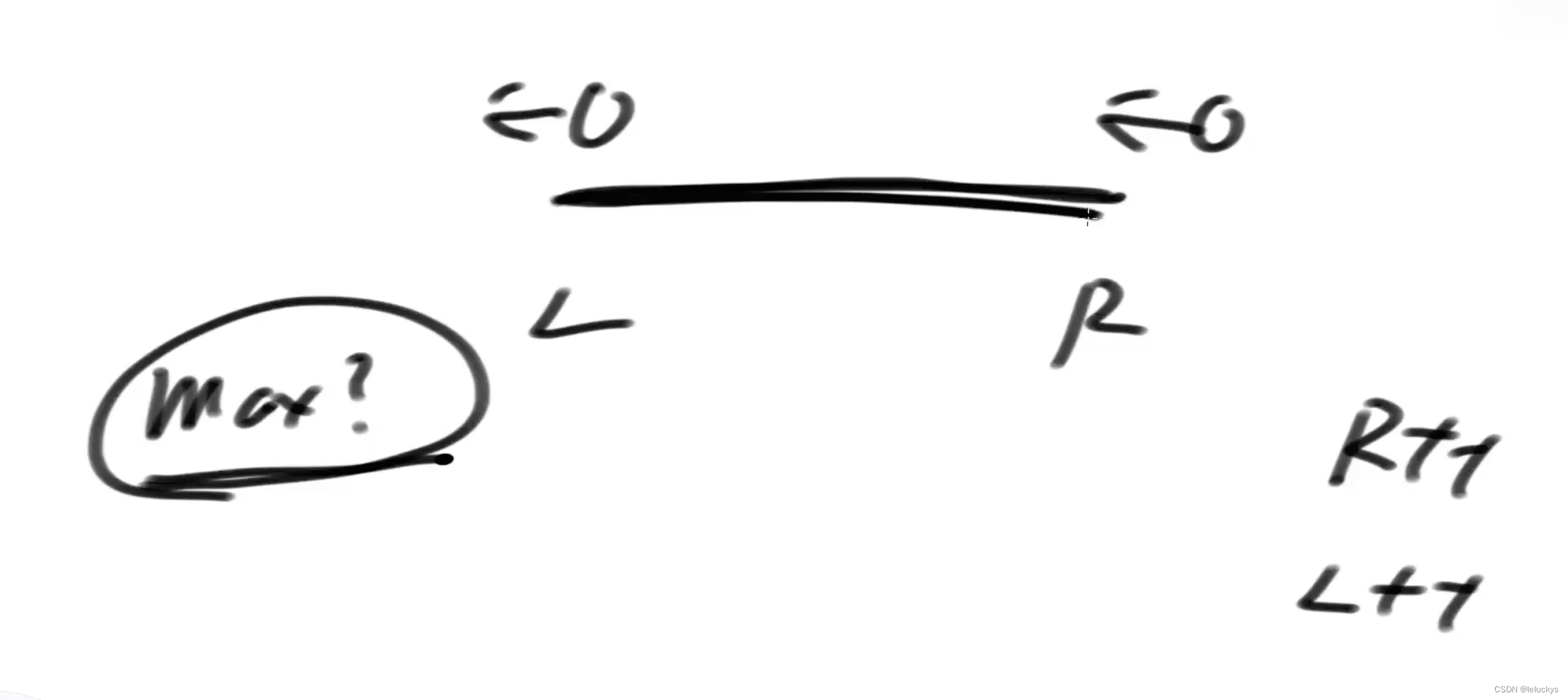
三 设计一个任何情况下端口的最大值
使用双端队列,队列遵循的原则是从头部到尾部的值是从大到小的更新策略,不管队列里面的值出去是从头部还是尾部出,一旦出去了就不再找回
1 R往右动的时候,队列动的规则是,当新进来的值比前面的值小直接从尾部进,当新进来的值比队列里面的值大,先从尾部弹出队列的值其不要了,再把大于他的值压进去
3.1 R阔的情况
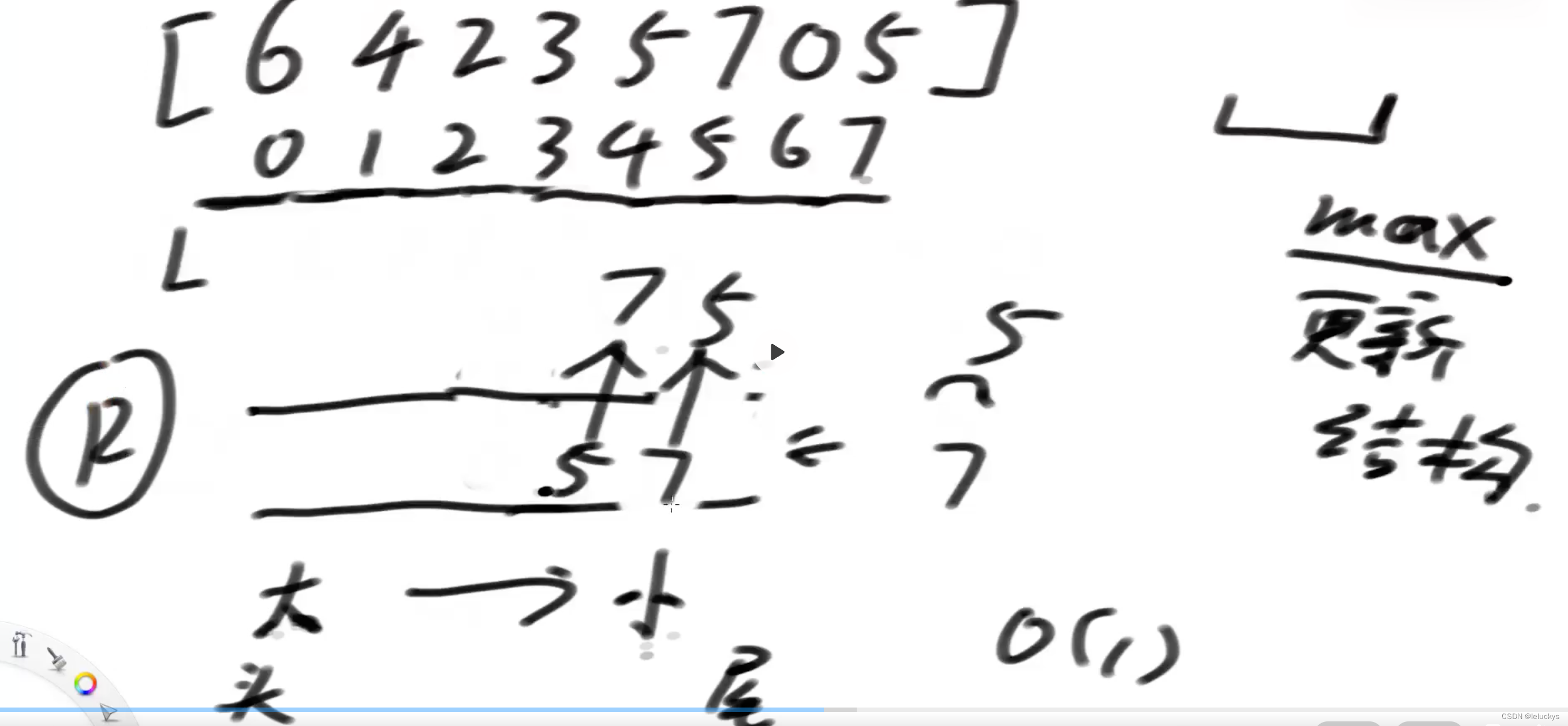
L的只能往右,在双端队列里面,为什么在R往右阔的时候,当前值比队列里面的值大的时候可以将之前进去的时抛弃掉,因为根据l和r只能往右阔,我当前的值是晚进来的,我一定是比刚从队列里面出去的值是晚过期的,所以可以这样做更新策略
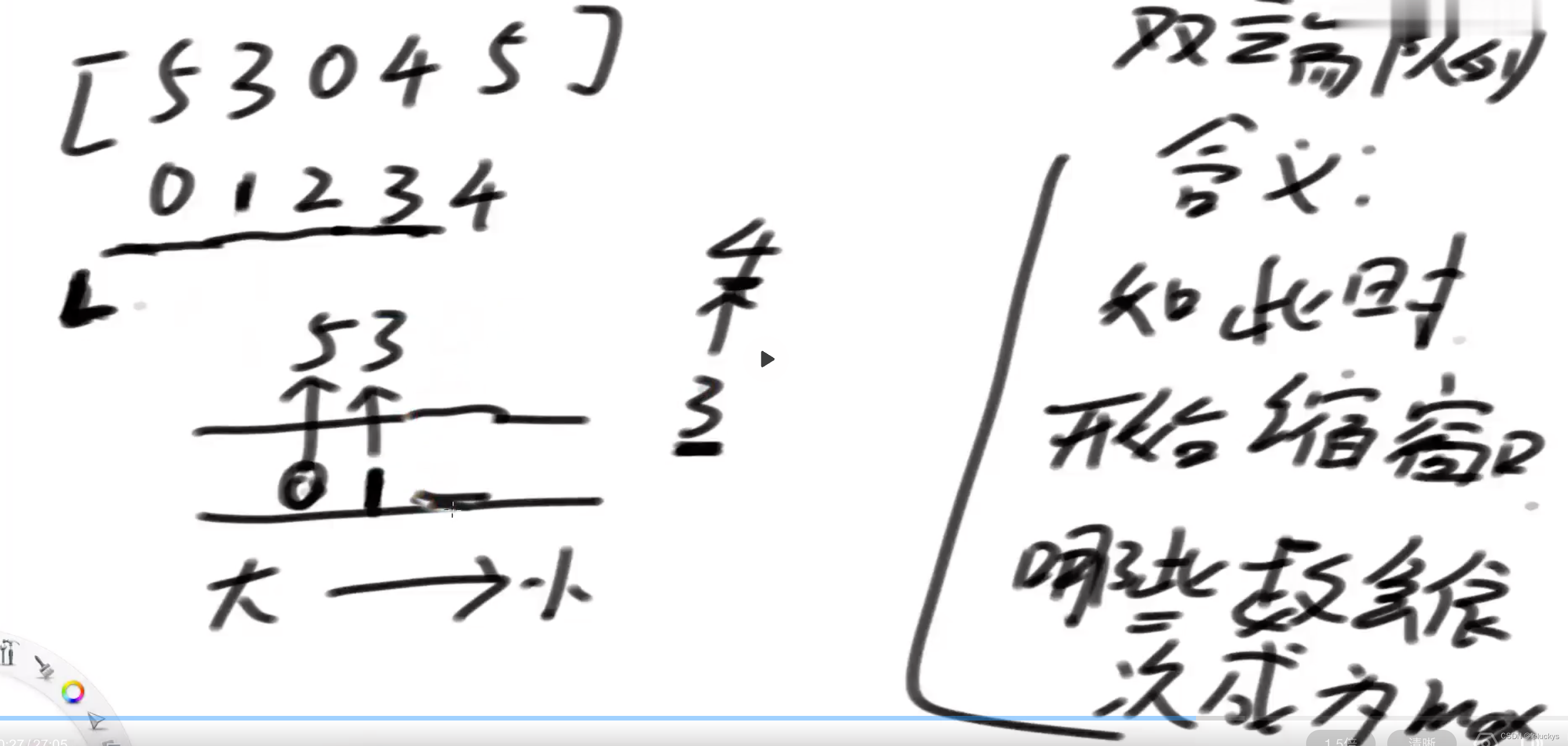
二 双端队列减的情况也就是L阔的情况
看双端队列里面的下标是否过期,过期的话就从头部弹出
更新的时间复杂度
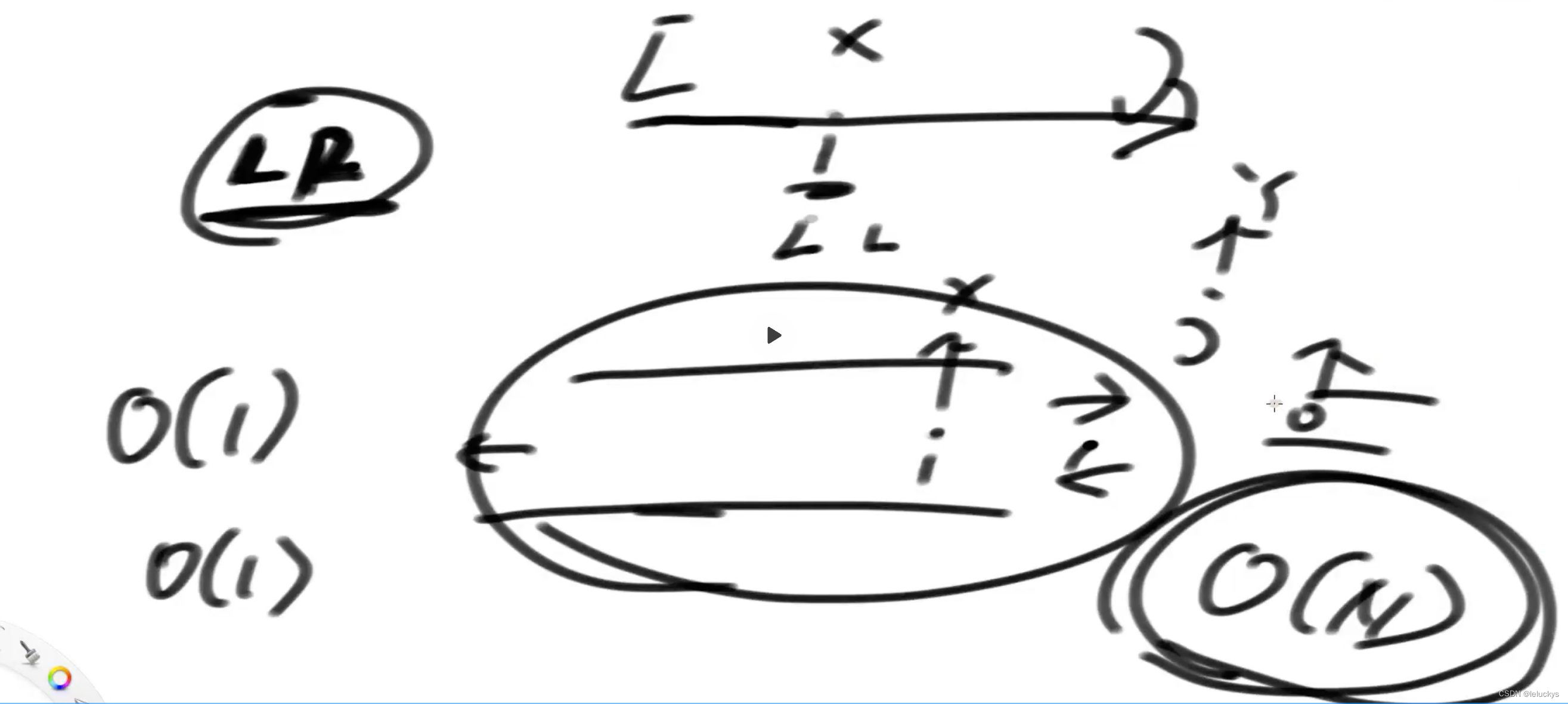
二 一个固定大小为W的窗口的最大值
2.1 描述
假设一个固定大小为W的窗口,依次划过arr, 返回每一次滑出状况的最大值 例如,arr = [4,3,5,4,3,3,6,7], W = 3 返回:[5,5,5,4,6,7]
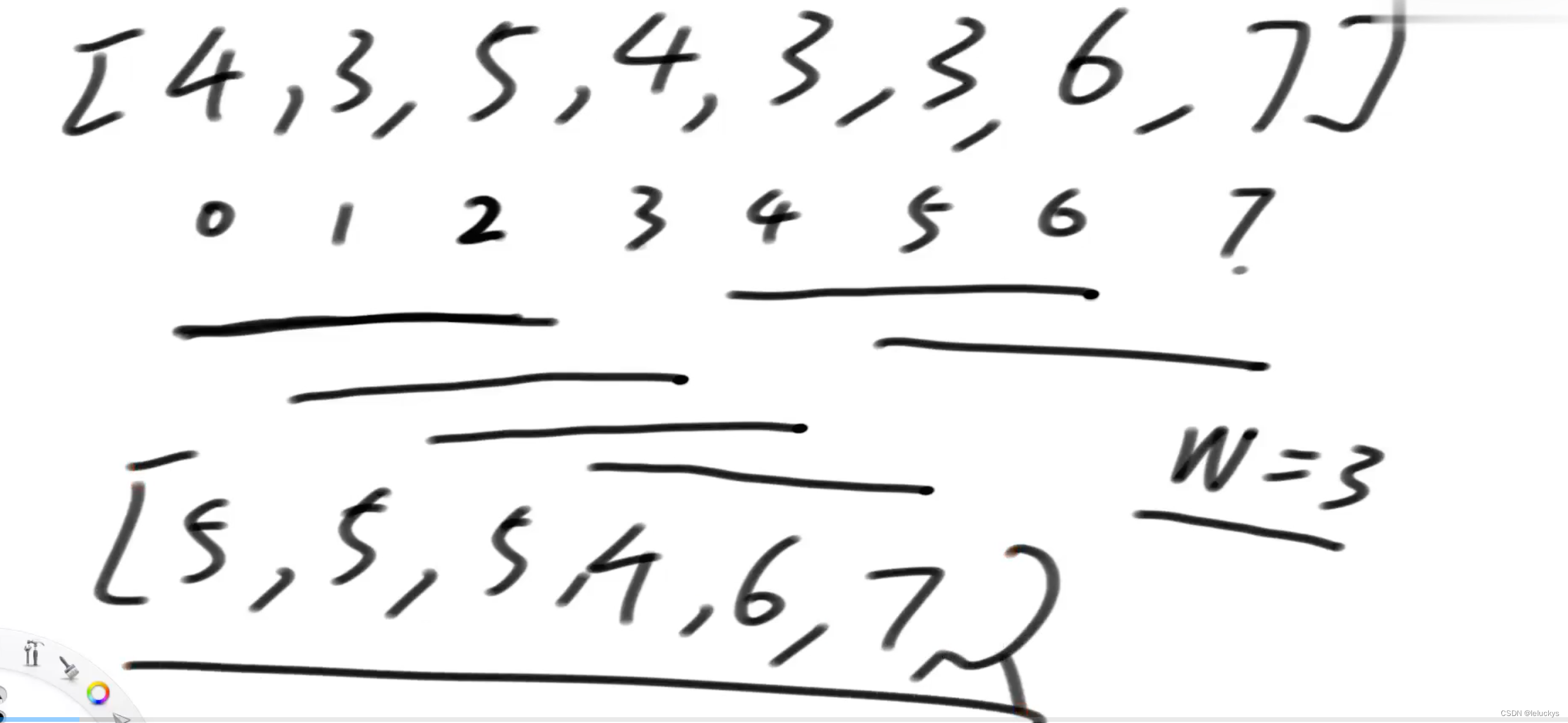
2.2 分析
分析应该收集的长度
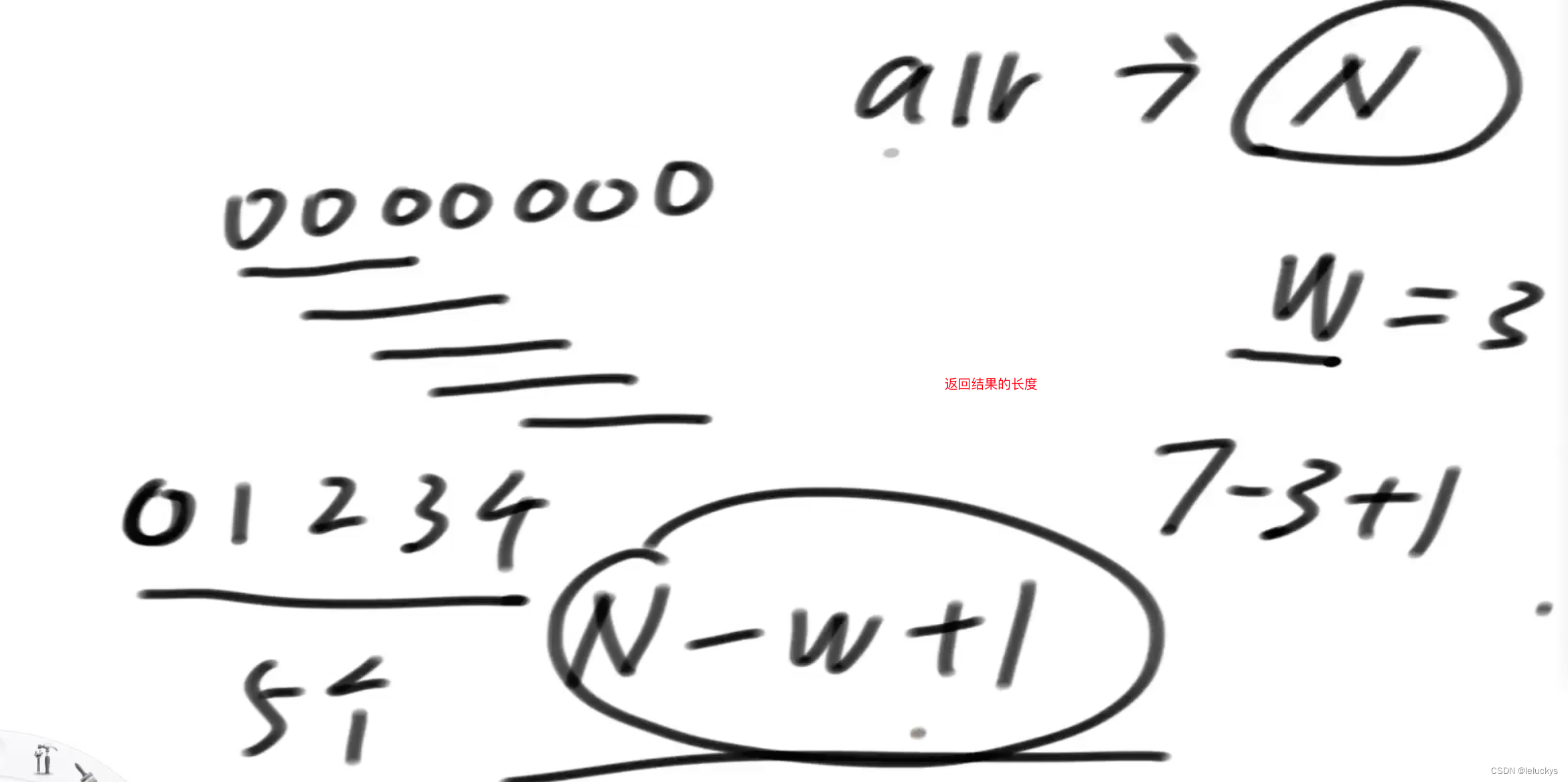
流程分析

2.3 代码
package class24;
import java.util.LinkedList;
public class Code01_SlidingWindowMaxArray {
// 暴力的对数器方法
public static int[] right(int[] arr, int w) {
if (arr == null || w < 1 || arr.length < w) {
return null;
}
int N = arr.length;
int[] res = new int[N - w + 1];
int index = 0;
int L = 0;
int R = w - 1;
while (R < N) {
int max = arr[L];
for (int i = L + 1; i <= R; i++) {
max = Math.max(max, arr[i]);
}
res[index++] = max;
L++;
R++;
}
return res;
}
public static int[] getMaxWindow(int[] arr, int w) {
if (arr == null || w < 1 || arr.length < w) {
return null;
}
// qmax 窗口最大值的更新结构
// 放下标
LinkedList<Integer> qmax = new LinkedList<Integer>();
int[] res = new int[arr.length - w + 1];
int index = 0;
for (int R = 0; R < arr.length; R++) {
while (!qmax.isEmpty() && arr[qmax.peekLast()] <= arr[R]) {
qmax.pollLast();
}
qmax.addLast(R);
if (qmax.peekFirst() == R - w) {
qmax.pollFirst();
}
if (R >= w - 1) {
res[index++] = arr[qmax.peekFirst()];
}
}
return res;
}
// for test
public static int[] generateRandomArray(int maxSize, int maxValue) {
int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) (Math.random() * (maxValue + 1));
}
return arr;
}
// for test
public static boolean isEqual(int[] arr1, int[] arr2) {
if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
return false;
}
if (arr1 == null && arr2 == null) {
return true;
}
if (arr1.length != arr2.length) {
return false;
}
for (int i = 0; i < arr1.length; i++) {
if (arr1[i] != arr2[i]) {
return false;
}
}
return true;
}
public static void main(String[] args) {
int testTime = 100000;
int maxSize = 100;
int maxValue = 100;
System.out.println("test begin");
for (int i = 0; i < testTime; i++) {
int[] arr = generateRandomArray(maxSize, maxValue);
int w = (int) (Math.random() * (arr.length + 1));
int[] ans1 = getMaxWindow(arr, w);
int[] ans2 = right(arr, w);
if (!isEqual(ans1, ans2)) {
System.out.println("Oops!");
}
}
System.out.println("test finish");
}
}
二 子数组中和小于sum的个数
2.1 描述
给定一个整型数组arr,和一个整数num 某个arr中的子数组sub,如果想达标,必须满足: sub中最大值 – sub中最小值 <= num, 返回arr中达标子数组的数量
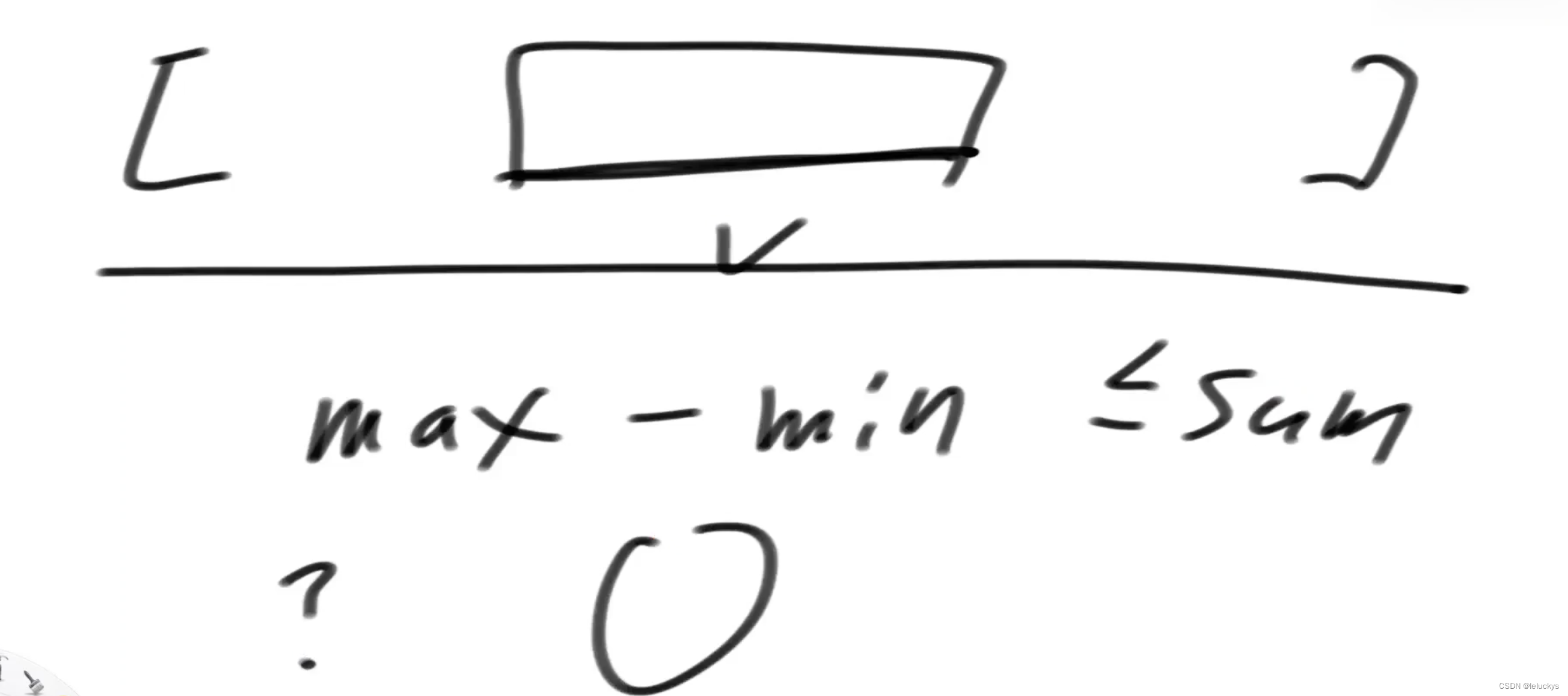
2.2 分析 暴力
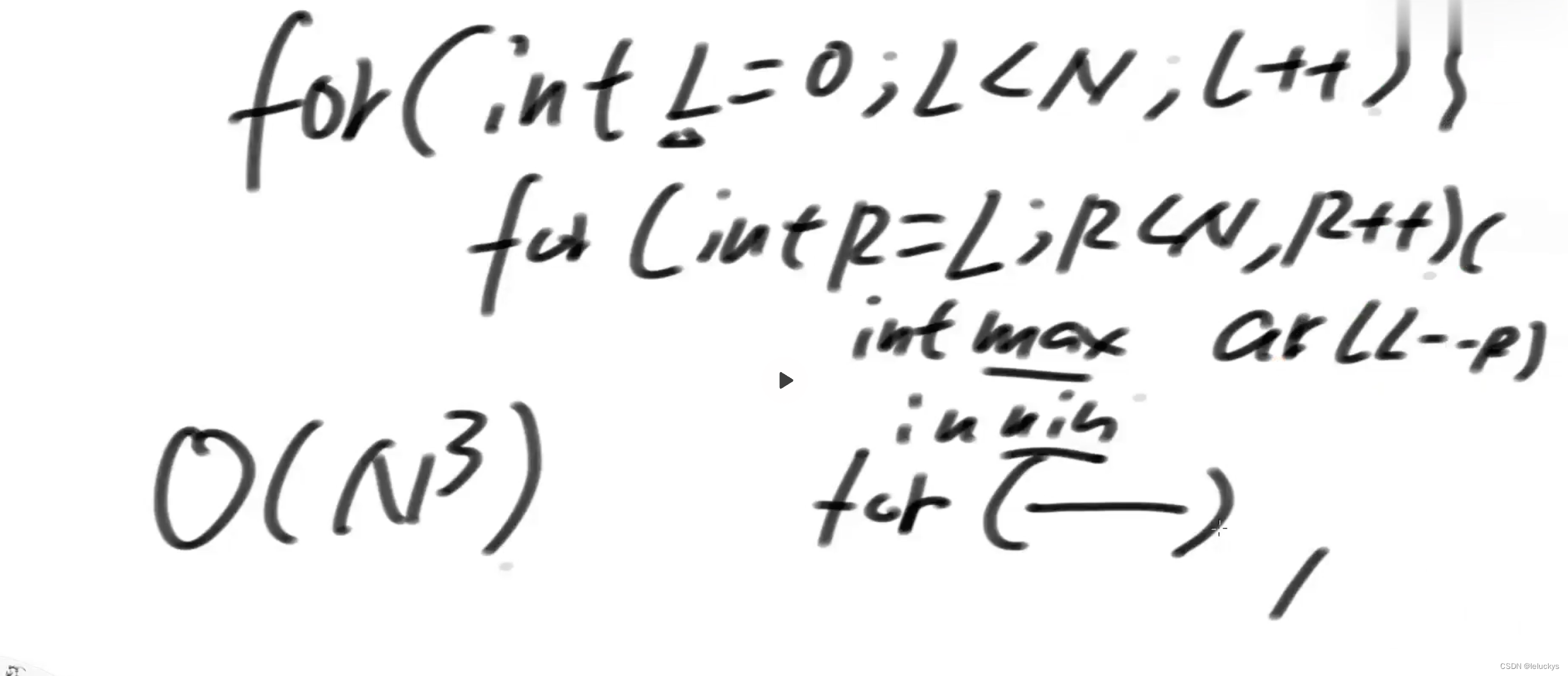 2.3 滑动窗口解析分析
2.3 滑动窗口解析分析
结论1 L到R范围内达标,那么它内部子数组也达标
一个 max-min范围的值小于sum可以推出 该max和min更小范围的子数组也大标,因为范围缩小了范围更靠近最后的差值更小
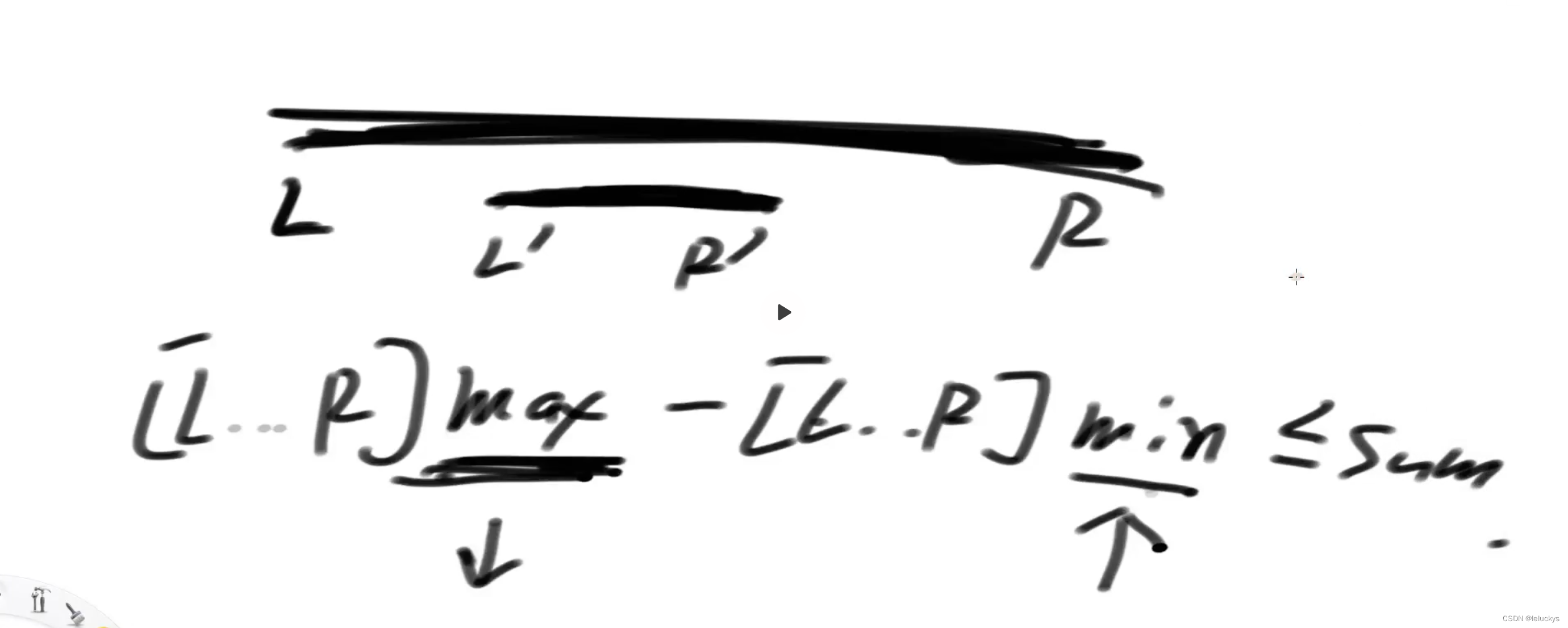

结论二 R到L范围不达标,那么l往左或者R往右也一定不达标

2.4 分析该题过程
一 两个队列 Qmax和 Qmin
二 滑动窗口的过程中会实时更新Qmax和 Qmin,当Qmax- Qmin 满足条件此时可以算出这个子数组满足条件的个数(由上面的两个结论推出)
三 接着l往右阔一个重复上面的过程
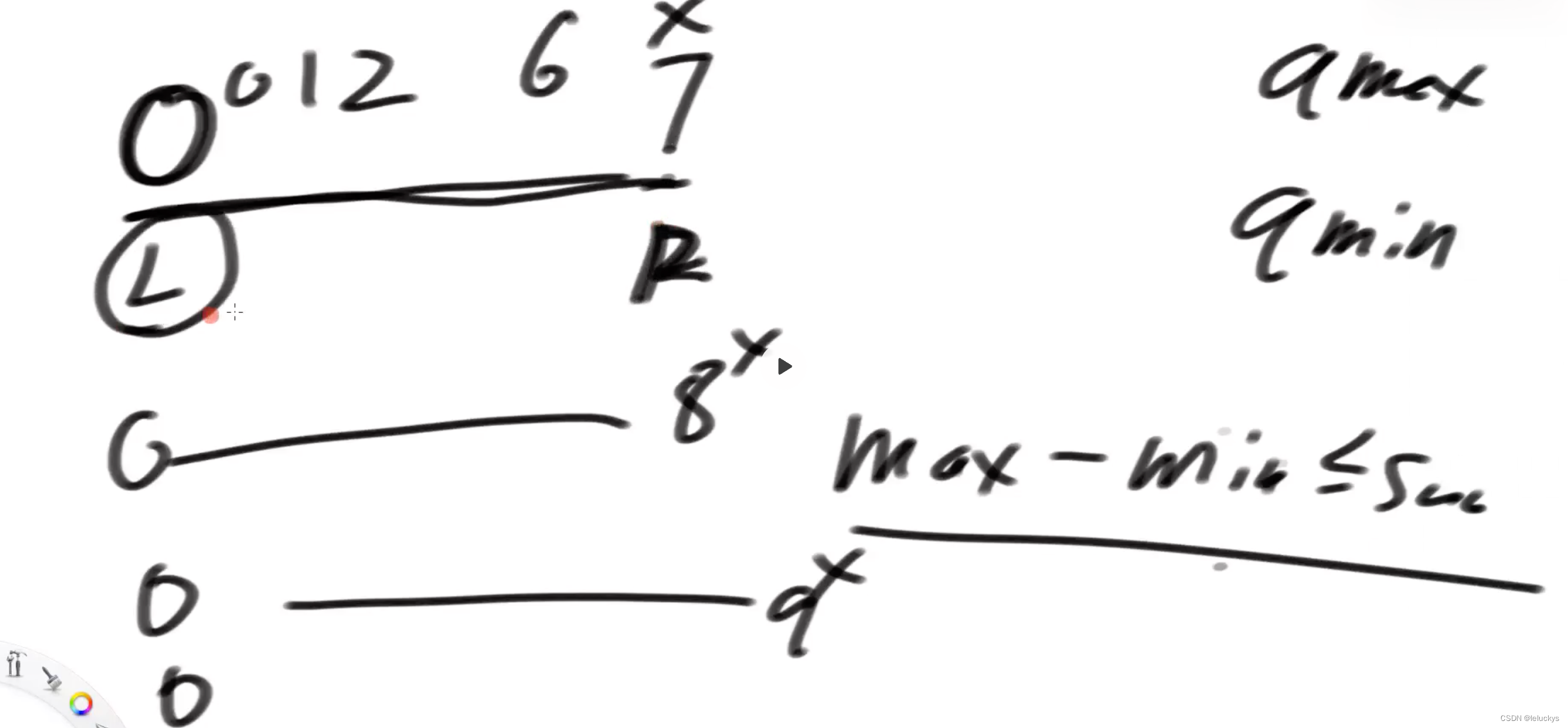
过期操作设置
//这块的过期是因为上面的l要开始++操作,滑出了窗口,但是在maxWindow,minWindow里面存的index正好是当前的l,那么下次++后这次就就要移除
if (maxWindow.peekFirst() == L) {
maxWindow.pollFirst();
}
if (minWindow.peekFirst() == L) {
minWindow.pollFirst();
}

2.5 代码
public static int num(int[] arr, int sum) {
if (arr == null || arr.length == 0 || sum < 0) {
return 0;
}
int N = arr.length;
int count = 0;
LinkedList<Integer> maxWindow = new LinkedList<>();
LinkedList<Integer> minWindow = new LinkedList<>();
int R = 0;
for (int L = 0; L < N; L++) {
//【l .....
//[l.....r (初次不达标了停止)
while (R < N) {
while (!maxWindow.isEmpty() && arr[maxWindow.peekLast()] <= arr[R]) {
maxWindow.pollLast();
}
maxWindow.addLast(R);
while (!minWindow.isEmpty() && arr[minWindow.peekLast()] >= arr[R]) {
minWindow.pollLast();
}
minWindow.addLast(R);
if (arr[maxWindow.peekFirst()] - arr[minWindow.peekFirst()] > sum) {
break;
} else {
R++;
}
}
count += R - L;
//这块的过期是因为上面的l要开始++操作,滑出了窗口,但是在maxWindow,minWindow里面存的index正好是当前的l,那么下次++后这次就就要移除
if (maxWindow.peekFirst() == L) {
maxWindow.pollFirst();
}
if (minWindow.peekFirst() == L) {
minWindow.pollFirst();
}
}
return count;
}三 加油站的良好出发点问题
3.1 描述


3.2 分析
将上面的数组进行加工,根据题目题目要求只要由不掉到0以下就行,就有当前加油站到下一个加油站的距离减去要耗的油,当当前数是否不小于0就表示满足题目要求

3.3 代码
package class24;
import java.util.LinkedList;
// 测试链接:https://leetcode.com/problems/gas-station
public class Code03_GasStation {
// 这个方法的时间复杂度O(N),额外空间复杂度O(N)
public static int canCompleteCircuit(int[] gas, int[] cost) {
boolean[] good = goodArray(gas, cost);
for (int i = 0; i < gas.length; i++) {
if (good[i]) {
return i;
}
}
return -1;
}
public static boolean[] goodArray(int[] g, int[] c) {
int N = g.length;
int M = N << 1;
int[] arr = new int[M];
for (int i = 0; i < N; i++) {
arr[i] = g[i] - c[i];
arr[i + N] = g[i] - c[i];
}
for (int i = 1; i < M; i++) {
arr[i] += arr[i - 1];
}
LinkedList<Integer> w = new LinkedList<>();
for (int i = 0; i < N; i++) {
while (!w.isEmpty() && arr[w.peekLast()] >= arr[i]) {
w.pollLast();
}
w.addLast(i);
}
boolean[] ans = new boolean[N];
for (int offset = 0, i = 0, j = N; j < M; offset = arr[i++], j++) {
if (arr[w.peekFirst()] - offset >= 0) {
ans[i] = true;
}
if (w.peekFirst() == i) {
w.pollFirst();
}
while (!w.isEmpty() && arr[w.peekLast()] >= arr[j]) {
w.pollLast();
}
w.addLast(j);
}
return ans;
}
}
第二种依次累加 看是否出现小于0的数
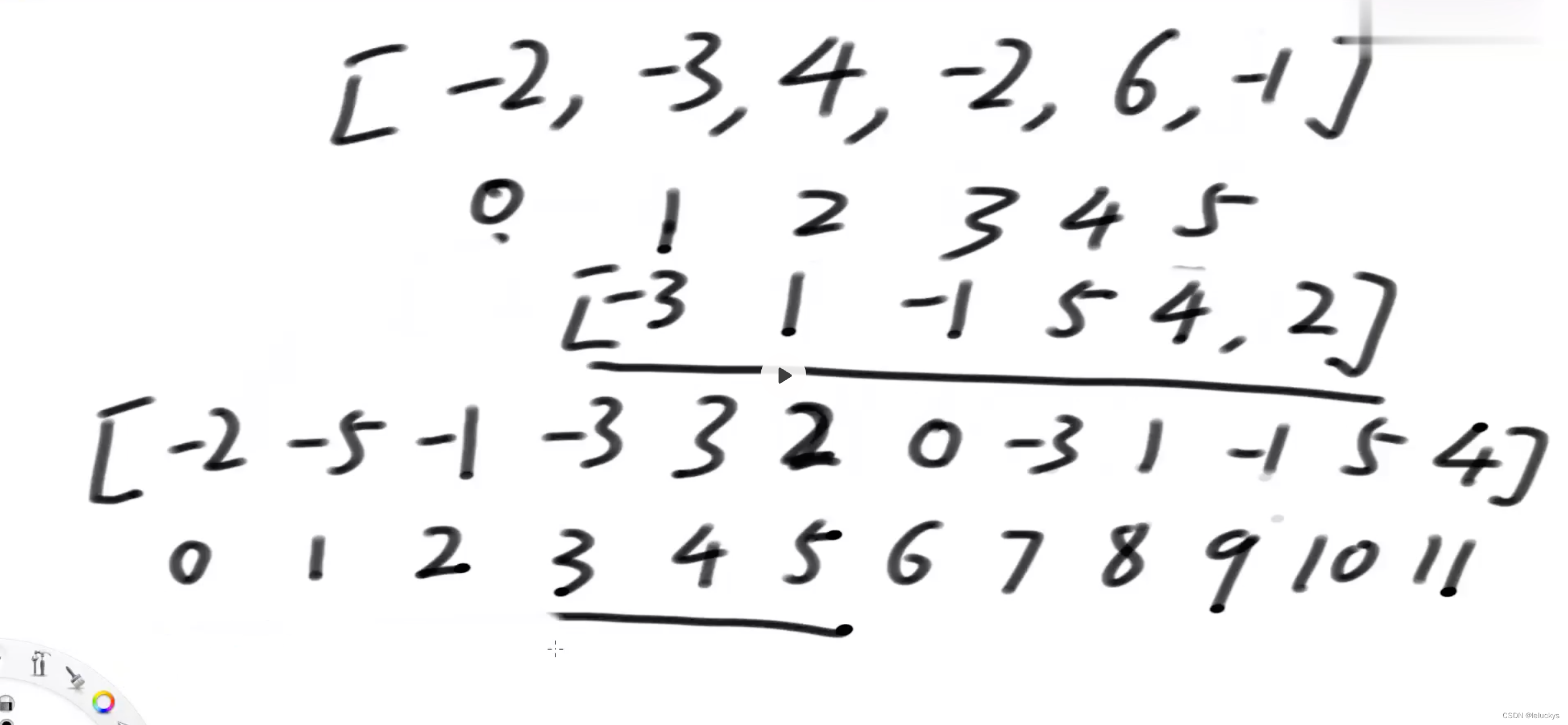
第一 组装一个原始数组的两倍长度的累加和
第二如何还原原是数组i到j的累加和 通过2被数组的j减去i就等于数组i到j的累加和

四 数组里面的数组成aim的张数最少是多少?
4.1 描述

4.2 分析
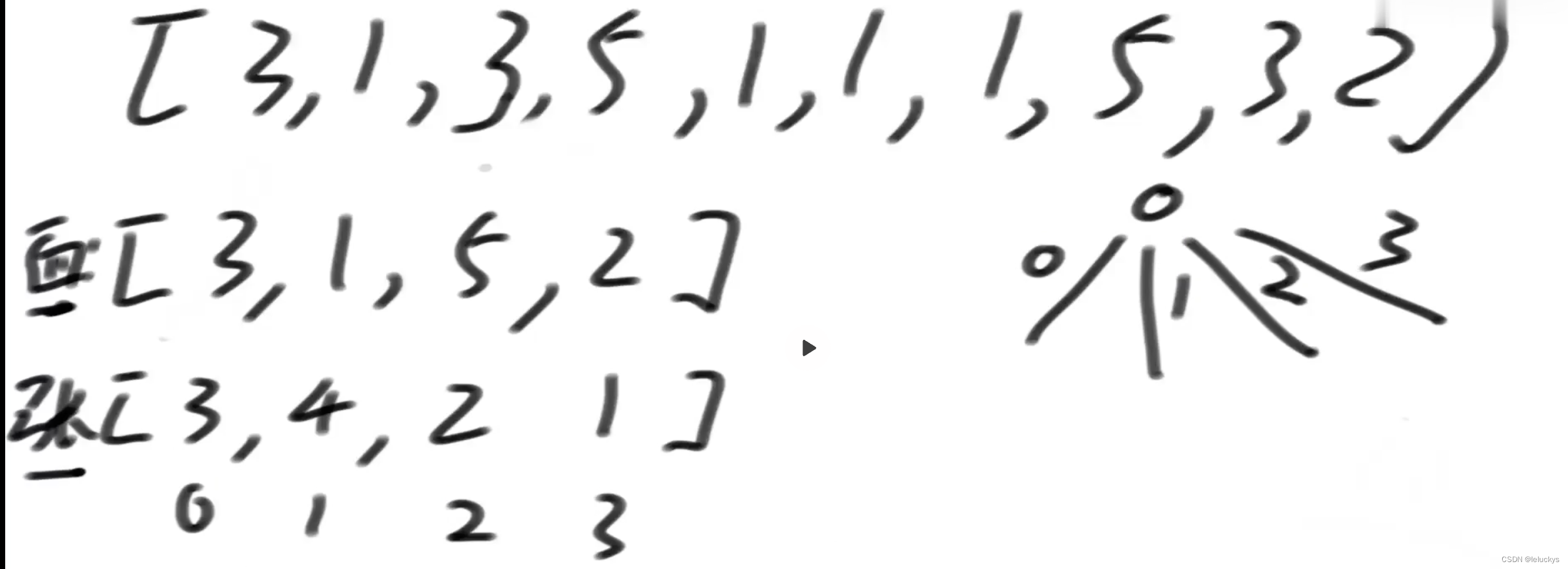



![【代码随想录】【算法训练营】【第57天】 [卡码99]岛屿数量 [卡码100]岛屿的最大面积](https://img-blog.csdnimg.cn/direct/dd7d7591a33c46e8a1f6e372ff7c1431.png)