目录
1 对数变换
1.1 对数变换的概念
1.2 对数变换实战
2 指数变换
2.1 指数变换的概念
2.2 指数变换实战
3 Box-Cox变换
3.1 Box-Cox变换概念
3.2 Box-Cox变换实战
1 对数变换
1.1 对数变换的概念
特征对数变换和指数变换是数据预处理中的两种常用技术,它们可以帮助改善数据的分布特性,从而提高某些模型的性能。
对数变换通常用于减少数据的偏斜性(skewness),它将原始数据的每个值转换为该值的自然对数或以10为底的对数。对于具有重尾分布的数据,对数变换时很好的处理方式。公式为:
![]()
1.2 对数变换实战
下面代码的目的是通过生成具有重尾分布的数据,并对其进行对数变换,来展示对数变换对数据分布的影响。
import numpy as np
import matplotlib.pyplot as plt
# 设置随机种子以获得可复现的结果
np.random.seed(0)
# 生成具有重尾分布的数据(例如,使用帕累托分布)
data = np.random.pareto(a=1, size=2000)
# 对数变换,这里使用10为底对数
# 为了避免对数变换中的问题,添加一个小的常数(例如1)
log_data = np.log10(data + 1)
# 绘制原始数据的直方图
plt.figure(figsize=(14, 5)) # 调整图形大小以便更清晰的展示
plt.subplot(1, 2, 1) # 1行2列的第一个图
plt.hist(data, bins=50, color='blue', alpha=0.7, log=True) # 使用对数刻度
plt.title('Original Data (Log Scale)')
plt.xlabel('Value') # 添加x轴标签
plt.ylabel('Frequency (log scale)') # 添加y轴标签,说明y轴是频率的对数刻度
# 绘制对数变换后数据的直方图
plt.subplot(1, 2, 2) # 1行2列的第二个图
plt.hist(log_data, bins=30, color='green', alpha=0.7) # 正常刻度
plt.title('Log-transformed Data')
plt.xlabel('Value') # 添加x轴标签
plt.ylabel('Frequency') # 添加y轴标签
# 显示图形
plt.tight_layout() # 调整布局以避免标签重叠
plt.show()下面是对代码的分析和对数变换前后作用的解释:
- 使用
np.random.pareto(a=2.0, size=2000)生成了2000个服从帕累托分布的数据点。帕累托分布是一种典型的重尾分布,其特点是大部分数据点集中在较小的值附近,而少数数据点是极端大的值。 - 对原始数据进行以10为底的对数变换,使用
np.log10(data + 1)。这里添加了1来避免对数函数在0处未定义的问题。
运行结果如下:

在原始数据的直方图上使用对数刻度,可以清晰地看到数据的重尾特性,即直方图的右侧有一个长尾,对数变换后的数据直方图可能看起来更加紧凑,极端大值的影响被减少
2 指数变换
2.1 指数变换的概念
指数变换通常用于处理具有极端值或非常不均匀分布的数据,它将原始数据的每个值转换为该值的指数函数,指数变换可以放大较小的值而压缩较大的值,有助于减少极端值的影响。公式为:
![]()
2.2 指数变换实战
指数变换主要应用与图像处理领域,可参考如下的文章:https://www.cnblogs.com/wancy/p/17819610.html
这段代码演示了如何对一组非正态分布的正值数据进行指数变换,并可视化变换前后的数据分布。
import numpy as np
import matplotlib.pyplot as plt
# 生成数据:使用gamma分布生成非正态分布的正值数据
data = np.random.gamma(shape=1.0, scale=1.0, size=1000)
# 归一化数据到[0, 1]区间
data_normalized = data / np.max(data)
# 应用指数变换
exp_data_normalized = np.exp(data_normalized - 1) # 减1保证变换后数据不会全为0
# 反归一化到原始数据的范围
exp_data = exp_data_normalized * np.max(data)
# 绘制原始数据的直方图
plt.figure(figsize=(10, 6))
plt.subplot(1, 2, 1)
plt.hist(data, bins=30, color='blue', alpha=0.7)
plt.title("Original Data")
# 绘制指数变换后数据的直方图
# 截断数据以避免过大的值
threshold = np.percentile(exp_data, 99) # 取99百分位数作为阈值
exp_data[exp_data > threshold] = threshold
plt.subplot(1, 2, 2)
plt.hist(exp_data, bins=30, color='green', alpha=0.7)
plt.title("Exponential Transformed Data")
# 添加坐标轴标签
plt.xlabel('Value')
plt.ylabel('Frequency')
# 显示图形
plt.tight_layout()
plt.show()下面是对代码的分析:
- 使用
numpy的random.gamma函数生成一组非正态分布的正值数据,这种分布通常产生偏斜的数据,具有重尾特性。 - 将数据归一化到[0, 1]区间。这是通过将每个数据点除以数据的最大值来实现的。归一化有助于在变换过程中保持数据的尺度一致性。
- 反归一化到原始数据的范围。通过将变换后的数据乘以原始数据的最大值来实现。

直方图显示了变换前后数据分布的对比,指数变换后的数据可能更加均匀或具有更小的偏斜度。
两种变换的使用场景和要求
这两种变换通常用于以下情况:
- 当数据具有非线性特征时,对数变换可以帮助线性化数据。
- 当数据的方差随着均值的增加而增加时(即方差与均值成正比),对数变换可以稳定方差。
- 当数据包含极端值或离群点时,指数变换可以帮助减少这些值的影响。
两种变换对数据要求:在应用这些变换之前,需要考虑数据的特性和模型的需求。例如,对数变换不适用于零或负值,因为对数函数在这些值上是未定义的。而指数变换则可以处理负值。
3 Box-Cox变换
3.1 Box-Cox变换概念
平方根变换和对数变换可以简单推广为Box-Cox变换。Box-Cox变换是一种在统计建模中常用的数据变换方法,由George E.P. Box和David Cox在1964年提出,用于处理连续的、正值的、偏斜分布的数据,以便它们更符合正态分布的要求。这种变换特别适用于线性回归模型中,当响应变量不满足正态分布时,通过变换可以使模型满足线性、正态性、独立性以及方差齐性的假设条件。
Box-Cox变换的一般形式为:

其中,y是原始数据,λ 是变换参数 。
box-cox变换的主要作用:是将数据进行归一化,使得数据更加符合统计假设。在实际应用中,box-cox变换常用于解决回归分析和方差分析中的数据不满足正态分布的问题,从而提高模型的准确度和可靠性。
box-cox变换优点:
- 提高模型预测准确性:将非正态分布的数据进行box-cox变换后,可以使数据更加符合正态分布,从而提高模型预测的准确性。
- 统计推断更可靠:在进行统计推断时,如果假设数据符合正态分布,但实际上并不符合,可能会导致结果的错误。通过box-cox变换将数据转换为正态分布后,统计推断的结果更加可靠。
- 处理异方差性:对于具有异方差性的数据,进行box-cox变换可以使数据更加平滑,从而更容易处理异方差性。
box-cox变换缺点:
- 数据必须为正数:box-cox变换要求数据必须为正数,因此无法处理包含负数的数据集。
- 参数需要选择:box-cox变换中的参数λ需要根据数据集进行选择,不同的λ值可能会导致不同的结果。因此,需要进行多次试验来找到最适合的λ值。例如,当 λ=0 时,Box-Cox变换退化为对数变换;当λ=−1 时为倒数变换;当λ=0.5 时为平方根变换。
- 数据范围影响变换效果:box-cox变换对于数据的范围敏感,如果数据集范围较小,可能会导致变换效果不佳,或者导致出现数值问题
3.2 Box-Cox变换实战
下面代码演示了如何使用Box-Cox变换对一组非正态分布的正值数据进行处理,并可视化原始数据和变换后数据的分布情况。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# 假设有一组非正态分布的正值数据
# 这里我们使用一个偏态分布的示例数据集
data = np.random.gamma(shape=2.0, scale=2.0, size=1000)
# 应用Box-Cox变换,并找到最优的lambda值
transformed_data, optimal_lambda = stats.boxcox(data)
# 打印最优的lambda值
print(f"Optimal lambda value: {optimal_lambda}")
# 绘制原始数据的直方图
plt.figure(figsize=(14, 6))
plt.subplot(1, 2, 1)
plt.hist(data, bins=30, color='blue', alpha=0.7)
plt.title("Original Data")
# 添加坐标轴标签
plt.xlabel('Value')
plt.ylabel('Frequency')
# 绘制变换后数据的直方图
plt.subplot(1, 2, 2)
plt.hist(transformed_data, bins=30, color='green', alpha=0.7)
plt.title(f"Box-Cox Transformed Data \n(lambda = {optimal_lambda})")
# 添加坐标轴标签
plt.xlabel('Value')
plt.ylabel('Frequency')
# 显示图形
plt.tight_layout()
plt.show()- 首先使用伽马分布生成一组非正态分布的正值数据,伽马分布是一种偏态分布,常用于模拟具有重尾分布的数据。
- 进一步使用
scipy.stats.boxcox函数对数据进行Box-Cox变换。该函数返回变换后的数据transformed_data和最优的lambda值optimal_lambda。最优的lambda值是通过极大似然估计得到的,用于确定最佳的Box-Cox变换形式。 - 最后使用
matplotlib库绘制原始数据和变换后数据的直方图。
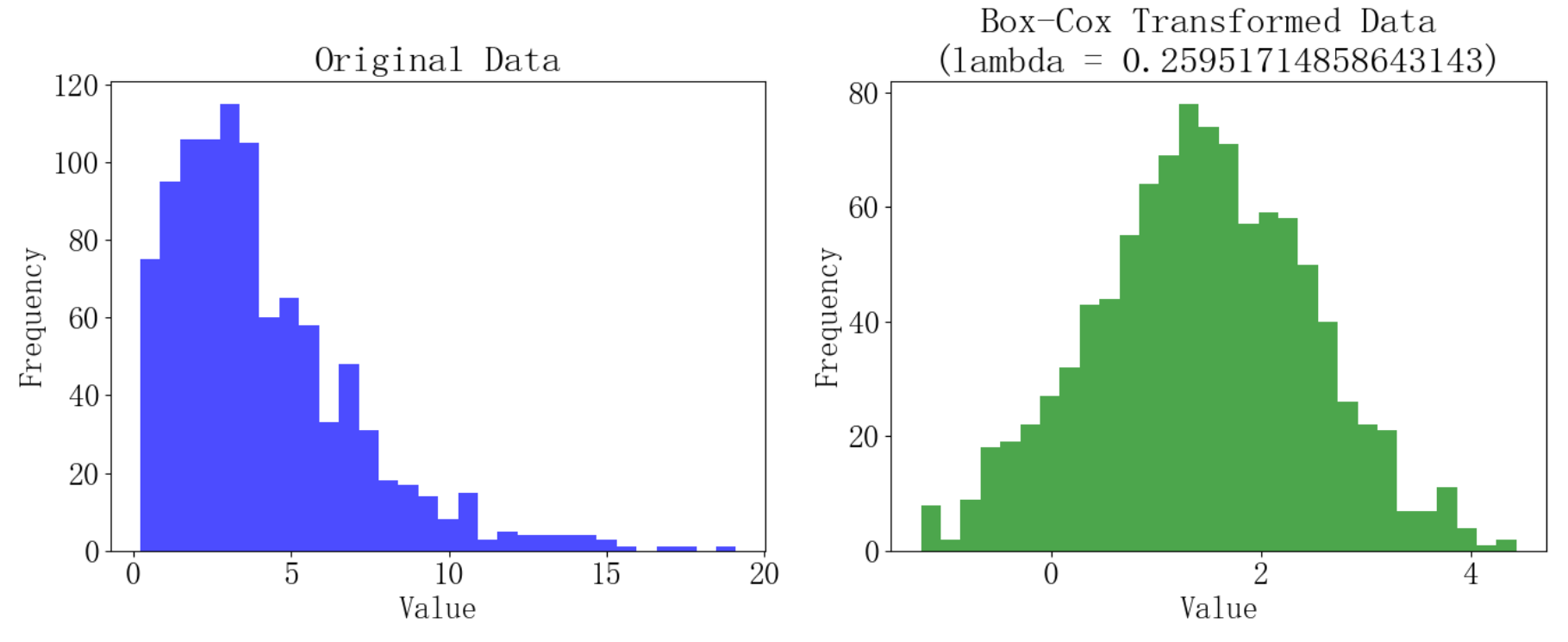
原始数据(伽马分布)具有偏态分布,Box-Cox变换旨在通过非线性变换减少数据的偏态,使数据更接近正态分布。



![AGI 之 【Hugging Face】 的【Transformer】的 [ Transformer 架构 ] / [ 编码器 ]的简单整理](https://img-blog.csdnimg.cn/direct/15ee1c3725ec414bb1f0864b4892249c.jpeg)