一、量化介绍

大型语言模型通常具有数十亿乃至上百亿参数，导致存储和计算成本极高，大多数下游用户难以进行微调。为了便于进一步部署，大模型的模型压缩成为关键的解决方案。

模型压缩目标：减少模型大小，加快训练速度，保持相同精度。

针对大模型主要是以量化为主。量化是一种将预训练模型中的权重从浮点数转换成低位数的技术。通常情况下，量化的精度是8位或更低。量化可以大大减少模型的存储空间和计算量，但可能对模型的性能产生一定的影响。

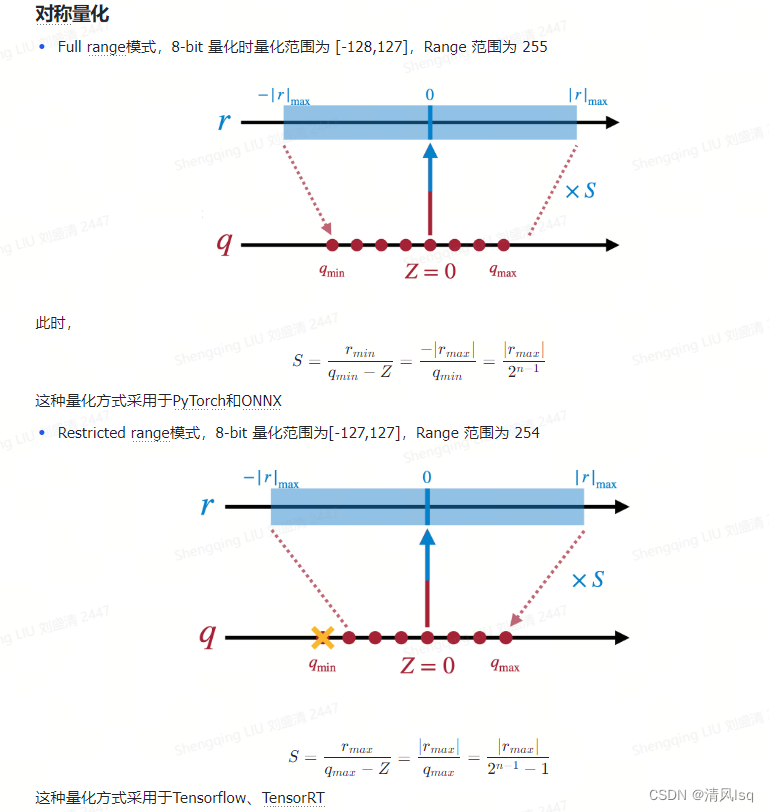
1. 对称量化：对称量化中浮点值的零点直接映射到量化值的零点，因此不需要其他参数来调整零点的映射的位置，与量化相关的参数只有缩放因子s。

2. 非对称量化：非对称量化有一个额外的参数Z调整零点的映射，这个参数通常称为零点。非对称量化表示的范围没有严格的限制，可以根据浮点值的范围，选取任意的想要表示的范围。因此非对称量化的效果通常比对称量化好，但是需要额外存储以及推理时计算零点相关的内容。

Tmax和Tmin代表实际数据的浮点数最大值、最小值，Qmax和Qmin代表量化后的最大值和最小值。

举例： 权重范围[-2.0,6.0]，即Tmax=6.0，Tmin=-2.0，用int8量化，定点量化值范围为[-128, 127]，即Qmax = 127，Qmin = -127，那么S和Z的求值过程如下：

二、量化原理计算过程

2.1 量化计算

1. 计算量化系数s,和偏移z.

量化的基本原理都是一样的，就是按照下面公式将浮点数转为一个区间内的整数， 尽可能的保持数据原有的分布不变。

2. 计算量化值

根据下面的公式可以计算得到量化的值q. 和反量化的浮点数据值r.

3. 计算的技巧优化

对称量化，z=0, 简化计算。

S=(max - min) / ((1 << 4) - 1); //得到量化系数

S=(max-min)/(2^n -1)

得到量化的数值：

q= (r-min)/S。 r：量化前的真实数据。实际的量化方式：(x[i*qk + 0 + j] - min)/S;

三、量化代码分析

3.1 llamacpp量化实现

使用时group wise进行量化，也就将需要量化的数据按照某一个维度进行分组，在一个组内找到最大，最小值，然后按照量化公式，将浮点数进行量化。

void quantize_row_q4_1_reference(const float * restrict x, block_q4_1 * restrict y, int k) {
    const int qk = QK4_1;

    assert(k % qk == 0);

    const int nb = k / qk; //分组量化， qk是组大小, 比如把一行32个数值的数据分成4组，每组包含8个数据，一个组内进行求最大最小值，然后进行一个一个组量化

    for (int i = 0; i < nb; i++) {
        float min = FLT_MAX;
        float max = -FLT_MAX;

        for (int j = 0; j < qk; j++) {
            const float v = x[i*qk + j];

            if (v < min) min = v;
            if (v > max) max = v;
        }

        const float d  = (max - min) / ((1 << 4) - 1);  //得到量化系数max-min/2^4-1 (4bit量化)
        const float id = d ? 1.0f/d : 0.0f;

        y[i].d = GGML_FP32_TO_FP16(d);
        y[i].m = GGML_FP32_TO_FP16(min); //保存这一组内的最小值，计算量化值的需要使用

        for (int j = 0; j < qk/2; ++j) {
        //对称的取两个值const float x0和const float x1：分别计算两个值的量化形式。
            const float x0 = (x[i*qk + 0    + j] - min)*id;
            const float x1 = (x[i*qk + qk/2 + j] - min)*id;
//保证最小值一定在4bit 表示的范围之内。const uint8_t xi0和const uint8_t xi1：四舍五入并确保量化值在0到15的范围内。
            const uint8_t xi0 = MIN(15, (int8_t)(x0 + 0.5f));
            const uint8_t xi1 = MIN(15, (int8_t)(x1 + 0.5f));
            
// y[i].qs[j]：将两个4位量化值合并为一个字节，第一个值存储在低4位，第二个值左移4位后存储在高4位。
            y[i].qs[j]  = xi0;
            y[i].qs[j] |= xi1 << 4;
        }
    }
}

3.2 难点解析：

const float x0 = (x[i*qk + 0 + j] - min)*id; const float x1 = (x[i*qk + qk/2 + j] - min)*id;

它的作用是将浮点数数组x中的值映射到量化的范围（这里是4位量化，即0到15）内。让我们逐步分析这两行代码：

1. const float x0 = (x[i*qk + 0 + j] - min) * id;

2. x[i*qk + 0 + j]：从量化块的开始位置（索引为i*qk）加上当前处理的元素索引j，获取原始浮点数x0的值。

3. min：量化块中的最小值，用于将数据归一化到0附近。

4. id：量化步长的逆，用于将归一化后的值映射到量化范围。

5. const float x1 = (x[i*qk + qk/2 + j] - min) * id;

6. x[i*qk + qk/2 + j]：从量化块的中间位置开始（索引为i*qk + qk/2），再加上当前处理的元素索引j，获取原始浮点数x1的值。这里假设qk是偶数，qk/2是量化块一半的位置。这两行代码的目的是将原始数据x中的值转换为相对于最小值min的偏移量，然后通过乘以逆量化步长id，将这些偏移量映射到量化的范围内。这样做的原因有：

7. 归一化：通过减去min，将数据范围转换到以0为中心的范围，这有助于量化后的数据分布更均匀。

8. 量化映射：通过乘以id，将归一化后的值映射到量化的整数范围内。由于是4位量化，范围是0到15。

为什么这样取值，还有以下考虑：

• 对称性：这段代码处理的是每对值x0和x1，它们分别位于量化块的前半部分和后半部分。这种方法利用了数据的对称性，可以减少计算量。

• 效率：通过同时处理两个值，可以减少循环迭代次数，提高量化过程的效率。

• 量化精度：通过计算每个量化块的最小值和最大值，然后根据这些极值确定量化步长，可以尽量保持量化块内数据的原始分布特性，从而在量化过程中保持较高的精度。

最后，这两行代码是量化过程中的一个步骤，将原始浮点数映射到量化的整数表示，以便后续可以以更紧凑的形式存储和处理。

3.3 llamacpp的反量化实现示例

void dequantize_row_q4_1(const block_q4_1 * restrict x, float * restrict y, int k) {
    static const int qk = QK4_1;

    assert(k % qk == 0);

    const int nb = k / qk;

    for (int i = 0; i < nb; i++) {
        const float d = GGML_FP16_TO_FP32(x[i].d); //量化系数
        const float m = GGML_FP16_TO_FP32(x[i].m); //min 最小值

        for (int j = 0; j < qk/2; ++j) {
            const int x0 = (x[i].qs[j] & 0x0F); //得到低位的量化值
            const int x1 = (x[i].qs[j] >>   4); //得到高位的量化值

            y[i*qk + j + 0   ] = x0*d + m; //按照公式反量化
            y[i*qk + j + qk/2] = x1*d + m;
        }
    }
}

3.2 llamcpp neon 加速的量化实现

void quantize_row_q8_0(const float * restrict x, void * restrict vy, int k) {
    assert(QK8_0 == 32); // 一组32个元素
    assert(k % QK8_0 == 0);
    const int nb = k / QK8_0; // 分组量化的组数

    block_q8_0 * restrict y = vy;
#if defined(__ARM_NEON)
    for (int i = 0; i < nb; i++) {
        float32x4_t srcv [8];
        float32x4_t asrcv[8];
        float32x4_t amaxv[8];

        for (int j = 0; j < 8; j++) srcv[j]  = vld1q_f32(x + i*32 + 4*j);
        for (int j = 0; j < 8; j++) asrcv[j] = vabsq_f32(srcv[j]);

        for (int j = 0; j < 4; j++) amaxv[2*j] = vmaxq_f32(asrcv[2*j], asrcv[2*j+1]);
        for (int j = 0; j < 2; j++) amaxv[4*j] = vmaxq_f32(amaxv[4*j], amaxv[4*j+2]);
        for (int j = 0; j < 1; j++) amaxv[8*j] = vmaxq_f32(amaxv[8*j], amaxv[8*j+4]);

        const float amax = vmaxvq_f32(amaxv[0]); //这32个数据的最大值。

        const float d = amax / ((1 << 7) - 1);
        const float id = d ? 1.0f/d : 0.0f;

        y[i].d = GGML_FP32_TO_FP16(d);

        for (int j = 0; j < 8; j++) {
            const float32x4_t v  = vmulq_n_f32(srcv[j], id); //量化值
            const int32x4_t   vi = vcvtnq_s32_f32(v);// 将量化后的浮点数四舍五入到最近的整数。

            y[i].qs[4*j + 0] = vgetq_lane_s32(vi, 0);
            y[i].qs[4*j + 1] = vgetq_lane_s32(vi, 1);
            y[i].qs[4*j + 2] = vgetq_lane_s32(vi, 2);
            y[i].qs[4*j + 3] = vgetq_lane_s32(vi, 3);
        }
    }
    }

3.2.1 步骤总结：

• 加载数据到NEON寄存器。

• 计算数据的绝对值。

• 通过比较操作找到最大值。

• 根据最大值计算量化步长。

• 使用量化步长将浮点数量化为整数。

• 存储量化结果。