在网格搜索中使用管道的工作原理与使用任何其他估计器都相同。
我们定义一个需要搜索的参数网络,并利用管道和参数网格构建一个GridSearchCV。不过在指定参数网格时存在一处细微的变化。我们需要为每个参数指定它在管道中所属的步骤。我们要调节的两个参数C和gamma都是SVC的参数,属于第二个步骤,我们给这个步骤的名称是“SVM”。为管道定义参数网格的语法是为每个参数指定步骤名称,后面加上__(双下划线),然后是参数名称。
因此,要想搜索SVC的C参数,必须使用“SVM__C”作为参数网格字典的键,对gamma参数同理:
param_grid={'svm__C':[0.001,0.01,0.1,1,10,100],
'svm__gamma':[0.001,0.01,0.1,1,10,100]}有了这个参数网格,我们就可以像平时一样使用GridSearchCV:
from sklearn.model_selection import GridSearchCV
grid=GridSearchCV(pipe,param_grid=param_grid,cv=5)
grid.fit(X_train,y_train)
print('最好交叉验证精度:{:.2f}'.format(grid.best_score_))
print('在测试集精度:{}'.format(grid.score(X_test,y_test)))
print('最优参数:{}'.format(grid.best_params_))与前面做的网格搜索不同,现在对于交叉验证的每次划分来说,仅使用训练部分对MinMaxScaler进行拟合,测试部分的信息没有泄露到参数搜索中。
import matplotlib.pyplot as plt
mglearn.plots.plot_proper_processing()
plt.show()
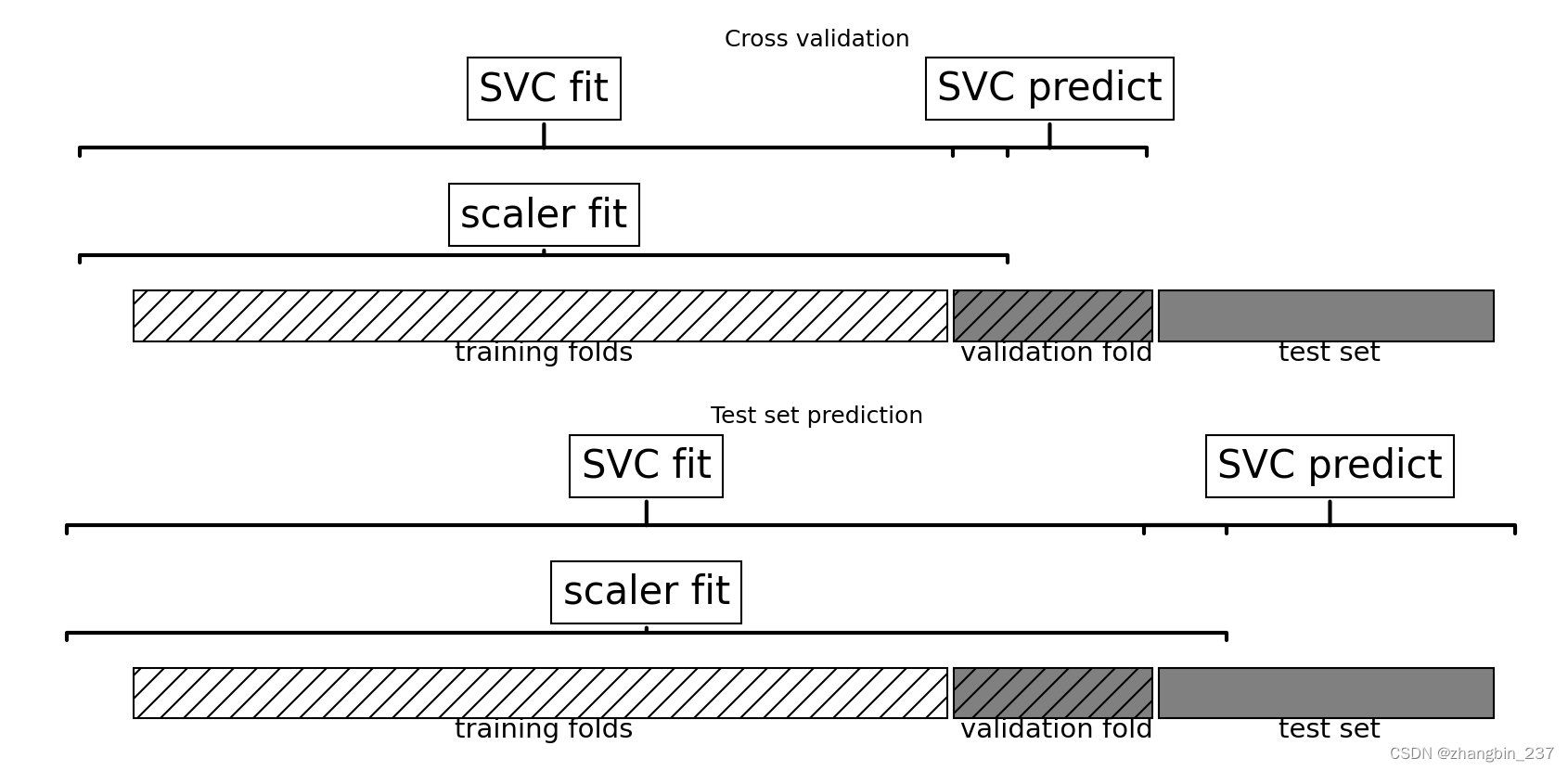
在交叉验证中,信息泄露的影响大小取决于预处理步骤的性质。
使用测试部分来估计数据的范围,通常不会产生可怕的影响,但在特征提取和特征选择中使用测试部分,则会导致结果的显著差异。
举例说明信息泄露:
我们考虑一个假想的回归任务,包含从高斯分布中独立采样的100个样本与10000个特征。我们还从高斯分布中对响应进行采样:
import numpy as np
rnd=np.random.RandomState(seed=0)
X=rnd.normal(size=(100,10000))
y=rnd.normal(size=(100,0))考虑到我们创建数据集的方式,数据X与目标y之间其实是没有任何联系的(他们是独立的),所以应该是不可能从这个数据集中学到任何内容。
现在我们完成下面的工作:首先利用SelectPercentile特征选择从10000个特征中选择信息量最大的特征,然后利用交叉验证对Ridge回归进行评估:
from sklearn.feature_selection import SelectPercentile,f_regression
select=SelectPercentile(score_func=f_regression,percentile=5).fit(X,y)
X_selected=select.transform(X)
print('X_selected.shape:{}'.format(X_selected.shape))
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import Ridge
print('交叉验证R2(Ridge):{}'.format(np.mean(cross_val_score(Ridge(),X_selected,y,cv=5))))
交叉验证计算得到的为0.91,表示是一个非常好的模型。
这显然是不对的,因为我们的数据是完全随机的。这里的特征选择从10000个随机特征中选出了与目标相关性非常好的一些特征。
由于我们在交叉验证之外对特征选择进行拟合,所以它能够找到在训练部分和测试部分都相关的特征。从测试部分泄露出去的信息包含的信息量非常大,导致得到了非常不切实际的结果。
我们将这个结果与正确的交叉验证(使用管道的)进行对比:
pipe=Pipeline([('slect',SelectPercentile(score_func=f_regression,percentile=5)),('ridge',Ridge())])
print('交叉验证R2(管道链):{}'.format(np.mean(cross_val_score(pipe,X,y,cv=5))))

这一次我们得到了负数的分数,这表示模型很差。利用管道,特征选择现在位于交叉验证循环内部。也就是说,仅使用了数据的训练部分来选择特征,而不使用测试部分。特征选择找到的特征在训练集中与目标相关,但是由于数据是完全随机的,这些特征在测试集中并不与目标相关。
在这个例子中,修正特征选择中的数据泄露问题,结论也由“模型表现很好”变为“模型根本没有效果”。