补题链接
https://www.luogu.com.cn/contest/178895#problems
A. 签到题
忽略掉大小为1的环,答案是剩下环的大小和减环的数量
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=1e6;
int n,a[N+5],cnt[N],ans;
bool vis[N];
int main(){
sci(n);
assert(1<=n && n<=N);
rep(i,1,n){
sci(a[i]);
cnt[a[i]]++;
}
rep(i,1,n){
assert(cnt[i]==1);
}
rep(i,1,n){
if(a[i]==i || vis[i])continue;
ans--;
for(int j=i;!vis[j];j=a[j]){
vis[j]=1;
ans++;
}
}
pte(ans);
return 0;
}E. 旅行(构造)
考虑怎么把一个点连的边都用完,然后递归到n-1个点的情况即可
这里的做法是,从1号点开始走,先去3再回来,再去4再回来,直到去n再回来
然后从1去2,然后解决n-1个点的情况,然后从2回1
递归
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=1e6,M=N+5;
int c,n;
vector<int>p;
void sol(int x){
p.pb(x);
rep(i,x+2,n){
p.pb(i);
p.pb(x);
}
if(x+1<=n){
sol(x+1);
p.pb(x);
}
}
int main(){
sci(n);
assert(2<=n && n<=1000);
sol(1);
int sz=SZ(p);
rep(i,0,sz-1){
printf("%d%c",p[i]," \n"[i==sz-1]);
}
return 0;
}for循环
注意到剩的i+1到i的边不必急着回来,可以最后从n->n-1->...->1统一回来
// 这是一份标程
#include<iostream>
using namespace std;
int main() {
int n; cin >> n;
for(int i = 1; i <= n; i++) {
cout << i << ' ';
for(int j = i + 2; j <= n; j++) {
cout << j << ' ' << i << ' ';
}
}
for(int i = n - 1; i > 0; i--) {
cout << i << ' ';
}
return 0;
}I. 三元环计数(组合数学/bitset)
我是不动脑子没有视力的算竞选手,看到三元环当然是bitset大力出奇迹啦
注意到题目给的竞赛图,也就是任意两个点之间都有边
所以任取三个点,只有两种情况,
一种是三元环,
一种是存在一个点a,a指向b,a指向c
用C(n,3)减去第二种情况即可
组合数学
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=4e3+10;
int t,n,v;
char s[N];
ll ans;
int main(){
sci(n);
assert(3<=n && n<=4000);
ans=1ll*n*(n-1)*(n-2)/6;
rep(i,1,n){
scanf("%s",s+1);
int m=strlen(s+1);
assert(m==n);
int v=0;
rep(j,1,n){
v+=(s[j]-'0');
}
ans-=1ll*v*(v-1)/2;
}
ptlle(ans);
return 0;
}bitset
n=4000,O(n^3/w)也能过真是大力出奇迹了…
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=4e3+10;
int n;
bitset<N>a[N],b[N];
char s[N];
ll ans;
int main(){
sci(n);
assert(3<=n && n<=4000);
rep(i,1,n){
scanf("%s",s+1);
rep(j,1,n){
assert(s[i]!='1');
if(s[j]=='1')a[i].set(j);
else{
if(i!=j)b[i].set(j);
}
}
}
rep(i,1,n){
rep(j,1,n){
if(a[i].test(j))ans+=(b[i]&a[j]).count();
//printf("i:%d j:%d ans:%lld\n",i,j,ans);
}
}
ptlle(ans/3);
return 0;
}B. 魔杖(dp)
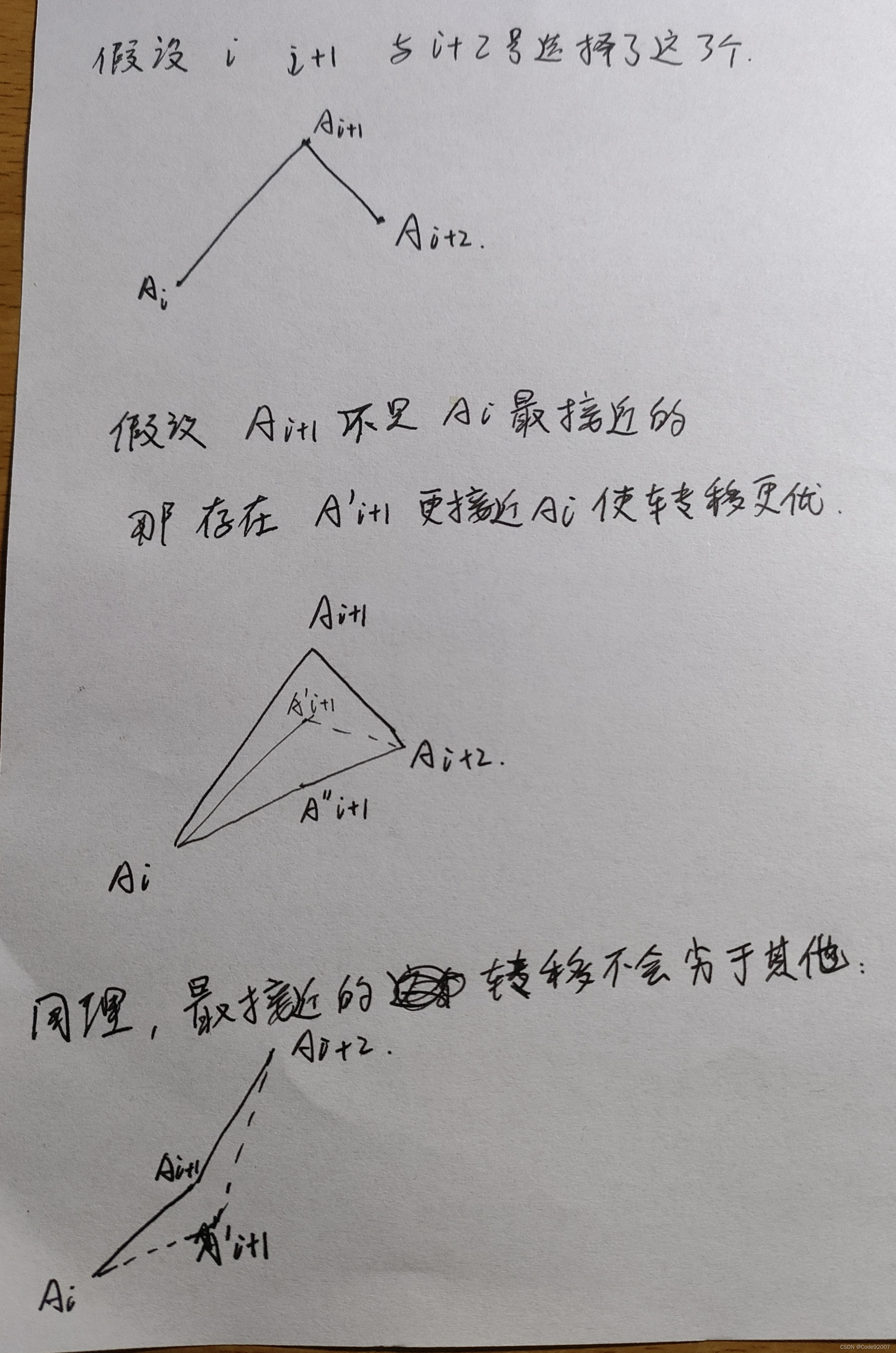
注意到每个值只可能由上一行与这个值最相邻的两个值转移,复杂度O(nm)
也就是要么从小于等于里最大的转移,要么从大于等于里最小的转移
朴素dp
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=105,M=2e4+10;
const ll INF=0x3f3f3f3f3f3f3f3fll;
int n,m,a[N][M];
ll dp[N][M];
int main(){
sci(n);sci(m);
assert(2<=n && n<=100 && 1<=m && m<=2e4);
rep(i,1,n){
rep(j,1,m){
sci(a[i][j]);
assert(1<=a[i][j] && a[i][j]<=1e9);
}
sort(a[i]+1,a[i]+m+1);
}
memset(dp,INF,sizeof dp);
rep(i,1,m)dp[1][i]=0;
rep(i,2,n){
int p=1;
rep(j,1,m){
while(p<=m && a[i-1][p]<=a[i][j])p++;
//printf("i:%d j:%d p:%d\n",i,j,p);
for(auto &x:{p-1,p}){
if(1<=x && x<=m){
dp[i][j]=min(dp[i][j],dp[i-1][x]+abs(a[i][j]-a[i-1][x]));
}
}
//printf("i:%d j:%d dp:%lld\n",i,j,dp[i][j]);
}
}
ptlle(*min_element(dp[n]+1,dp[n]+m+1));
return 0;
}如果没有注意到这个性质的话,可以用线段树或单调队列优化转移
但是注意到从上一行比当前值小的转移,就是dp[i][k]=min(dp[i-1][j]+a[i][k]-a[i-1][j])
从上一行比当前值大的转移,就是dp[i][k]=min(dp[i-1][j]+a[i-1][j]-a[i][k])
所以分别,正序双指针维护上一行dp[i-1][j]-a[i-1][j],逆序双指针维护上一行dp[i-1][j]+a[i-1][j]
双指针dp
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=105,M=2e4+10;
const ll INF=0x3f3f3f3f3f3f3f3fll;
int n,m,a[N][M];
ll dp[N][M];
int main(){
sci(n);sci(m);
assert(2<=n && n<=100 && 1<=m && m<=2e4);
rep(i,1,n){
rep(j,1,m){
sci(a[i][j]);
assert(1<=a[i][j] && a[i][j]<=1e9);
}
sort(a[i]+1,a[i]+m+1);
}
memset(dp,INF,sizeof dp);
rep(i,1,m)dp[1][i]=0;
rep(i,2,n){
int p=1;
ll now=1e18;
rep(j,1,m){
while(p<=m && a[i-1][p]<=a[i][j]){
now=min(now,dp[i-1][p]-a[i-1][p]);
p++;
}
dp[i][j]=min(dp[i][j],now+a[i][j]);
}
p=m;
now=1e18;
per(j,m,1){
while(p>=1 && a[i-1][p]>=a[i][j]){
now=min(now,dp[i-1][p]+a[i-1][p]);
p--;
}
dp[i][j]=min(dp[i][j],now-a[i][j]);
}
}
ptlle(*min_element(dp[n]+1,dp[n]+m+1));
return 0;
}G. 回忆(扫描线入门题)
首先保证两个区间有交集,
按端点排个序然后扫描线,在l的时候把线段加进multiset,r之后删掉
然后答案分两种,相交的和包含的
相交的,[1,50]和[10,100],答案=(100-1)-(50-10)=100+10-(1+50)
就是两端点之和减去multiset里最小的两端点之和
然后包含的是两端点之差减最小之差,
包含的情况是之前加的线段的右端点更靠右,
形如[1,100]和[10,50],是100-1-(50-10)
所以用multiset里最大的两端点之差减当前两端点之差
当然可以用线段树之类的数据结构写,但感觉没必要
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=2e5+10,M=2*N;
int n,l[N],r[N],x[M],c,ans;
vector<int>add[M],del[M];
multiset<int>in,in2;
int main(){
sci(n);
assert(1<=n && n<=200000);
rep(i,1,n){
sci(l[i]),sci(r[i]);
assert(1<=l[i] && l[i]<=r[i] && r[i]<=100000000);
x[c++]=l[i];x[c++]=r[i];
}
sort(x,x+c);c=unique(x,x+c)-x;
rep(i,1,n){
l[i]=lower_bound(x,x+c,l[i])-x;
r[i]=lower_bound(x,x+c,r[i])-x;
add[l[i]].pb(i);
del[r[i]].pb(i);
}
rep(i,0,c-1){
for(auto &v:add[i]){
int w=x[l[v]]+x[r[v]];
int w2=x[r[v]]-x[l[v]];
if(!in.empty()){
ans=max(ans,w-(*in.begin()));
}
if(!in2.empty()){
ans=max(ans,(*in2.rbegin())-w2);
//ans=max(ans,w2-(*in2.begin()));
}
in.insert(w);
in2.insert(w2);
}
for(auto &v:del[i]){
int w=x[l[v]]+x[r[v]];
int w2=x[r[v]]-x[l[v]];
in.erase(in.find(w));
in2.erase(in2.find(w2));
}
}
pte(ans);
return 0;
}H. 简单的平方串(kmp/exkmp/哈希)
枚举S+R的一半有多长,转化成判断s的[1,i]和[i+1,n]后者是否是前者的前缀的问题
这里是用exkmp求extend[i],当然这个玩意kmp也可以求,哈希也可以
如果S+R的一半已经超过了S原来的长度,
说明后面可以任意补a-z的字符,需要预处理26的幂的前缀和
kmp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 998244353;
const int N = 2e6 + 10;
const int M = 5e6 + 10;
int p26[M], pmt[N];
int main(int argc, char *argv[]) {
if(argc == 3) {
freopen(argv[1] + 1, "rb", stdin);
freopen(argv[2] + 1, "wb", stdout);
}
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
p26[0] = 1;
for(int i = 1; i < M; i++) {
p26[i] = (26LL * p26[i - 1] + 1) % mod;
}
int T; cin >> T;
while(T--) {
string s;int x, ans = 0;
cin >> s >> x;
if(x >= s.length())
ans = p26[(x - s.length()) / 2];
for(int i = 1, j = 0; i < s.length(); i++) {
while(j && s[i] != s[j]) j = pmt[j];
j += (s[j] == s[i]);
pmt[i + 1] = j;
}
for(int i = pmt[s.length()]; i; i = pmt[i]) {
if(i <= s.length() / 2 && x >= s.length() - i * 2) ans++;
}
ans %= mod;
cout << ans << '\n';
}
return 0;
}exkmp
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=2e6+10,M=5e6+10,mod=998244353;
int t,x,n,sum[M];
int net[N],ex[N];
char s[N];
void extkmppre(char s[],int len){
int i=0,j,pos;
net[0]=len;
while(i+1<len&&s[i]==s[i+1])i++;
net[1]=i,pos=1;
rep(i,2,len-1){
if(net[i-pos]+i<net[pos]+pos){
net[i]=net[i-pos];
}
else{
j=net[pos]+pos-i;
if(j<0)j=0;
while(i+j<len&&s[j]==s[i+j])j++;
net[i]=j,pos=i;
}
}
}
void extkmp(char s1[],char s2[],int l1,int l2){
int i=0,j,pos;
extkmppre(s2,l2);
while(i<l2&&i<l1&&s1[i]==s2[i])i++;
ex[0]=i,pos=0;
rep(i,1,l1-1){
if(net[i-pos]+i<ex[pos]+pos){
ex[i]=net[i-pos];
}
else{
j=ex[pos]+pos-i;
if(j<0)j=0;
while(i+j<l1&&j<l2&&s1[i+j]==s2[j])j++;
ex[i]=j,pos=i;
}
}
}
int main(){
sci(t);
assert(1<=t && t<=200000);
int bs=1;
sum[0]=1;
rep(i,1,M-1){
bs=26ll*bs%mod;
sum[i]=(sum[i-1]+bs)%mod;
}
int m=0;
while(t--){
scanf("%s",s);
sci(x);
n=strlen(s);
assert(1<=n && n<=2000000);
assert(0<=x && x<=5000000);
m+=n;
extkmp(s,s,n,n);
int ans=0;
rep(i,0,n-1){
if(i+ex[i]>=n && ex[i]<=i){//len=i
if(2*i<=n+x)ans++;
}
}
if(x>=n)ans=(ans+sum[(x-n)/2])%mod;
pte(ans);
}
assert(m<=3000000);
return 0;
}哈希
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 998244353;
int p26[5000006];
struct pii {
ll x, y;
pii(ll x = 0, ll y = 0) : x(x), y(y) {}
} ha[2000006], p[2000006];
pii operator + (pii a, pii b) {return pii((a.x + b.x) % mod, (a.y + b.y) % mod);}
pii operator + (pii a, int b) {return pii((a.x + b) % mod, (a.y + b) % mod);}
pii operator * (pii a, pii b) {return pii((a.x * b.x) % mod, (a.y * b.y) % mod);}
pii operator - (pii a, pii b) {return pii((a.x - b.x + mod) % mod, (a.y - b.y + mod) % mod);}
bool operator == (pii a, pii b) {return a.x == b.x && a.y == b.y;}
const pii base(131, 13331);
pii gethash(int L ,int R) {
return ha[R] - ha[L - 1] * p[R - L + 1];
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
p26[0] = 1;
for(int i = 1; i < 5000006; i++) {
p26[i] = (26LL * p26[i - 1] + 1) % mod;
}
p[0] = {1, 1};
for(int i = 1; i <= 2000000; i++) {
p[i] = p[i - 1] * base;
}
int T; cin >> T;
while(T--) {
string s; int x, ans = 0;
cin >> s >> x;
for(int i = 0; i < s.length(); i++) {
ha[i + 1] = ha[i] * base + s[i];
}
for(int i = (s.length() & 1); i < s.length() && i <= x; i += 2) {
int len = i + s.length();
len = s.length() - len / 2;
if(gethash(1, len) == gethash(s.length() - len + 1, s.length())) ans++;
}
if(x >= s.length()) ans = (ans + p26[(x - s.length()) / 2]) % mod;
cout << ans << '\n';
}
return 0;
}
解释
D. 地牢探索(二叉树种类数 卡特兰数)
其实不如直接暴力dp打个表找找规律

首先,分母是卡特兰数,卡特兰数是C(2n,n)/(n+1)

蓝色的是可以挂叶子的地方,对于n个点的每一种二叉树形态,都有n+1个挂叶子的地方
独立考虑每个有贡献的叶子,n个点能挂2n个儿子,已经用了n-1条边建树,所以还能挂n+1个
虽然挂完之后二叉树形态可能相同,但是产生贡献的叶子不一样
挂上叶子之后是n+1个点,所以n+1个点的所有二叉树形态总的叶子和是C(2n,n),
也就是n个点时,分子是C(2n-2,n-1)
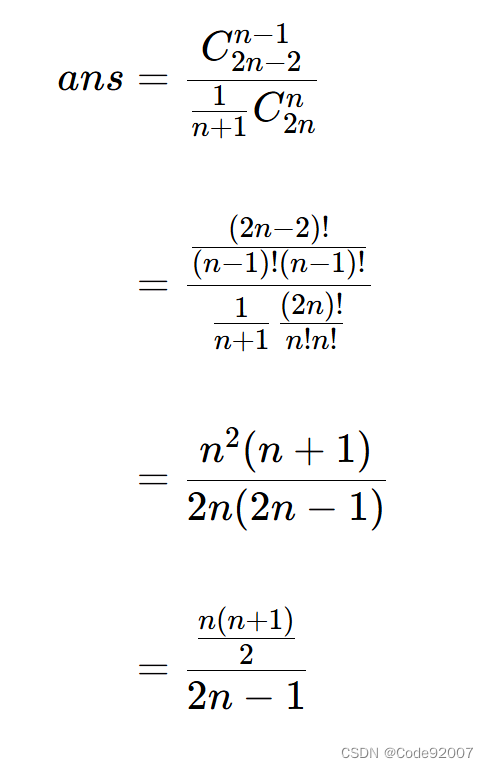
所以输出化简后的值即可,注意这个取模是2148473647,爆了int
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const ll mod=2148473647;
int n;
ll modpow(ll x,ll n,ll mod){
ll res=1;
for(;n;n/=2,x=1ll*x*x%mod){
if(n&1)res=1ll*res*x%mod;
}
return res;
}
int main(){
sci(n);
assert(1<=n && n<=1000000000);
ll x=1ll*n*(n+1)/2;
x%=mod;
ll y=modpow(2ll*n-1,mod-2,mod);
x=1ll*x*y%mod;
ptlle(x);
return 0;
}C. 静水监狱(计算几何)
判一下在凸包上还是凸包内还是凸包外,这里是用的二分,其实暴力找复杂度也够
对于在凸包内的情况,最近的距离的那条边是不会变的,
假设最近的距离是a,那么求一下时间就是
换元令u=v0+ks解一下定积分就做完了,答案是
当然可以参考一下泽与给的微分方程式子,重生之我在院赛学微分方程
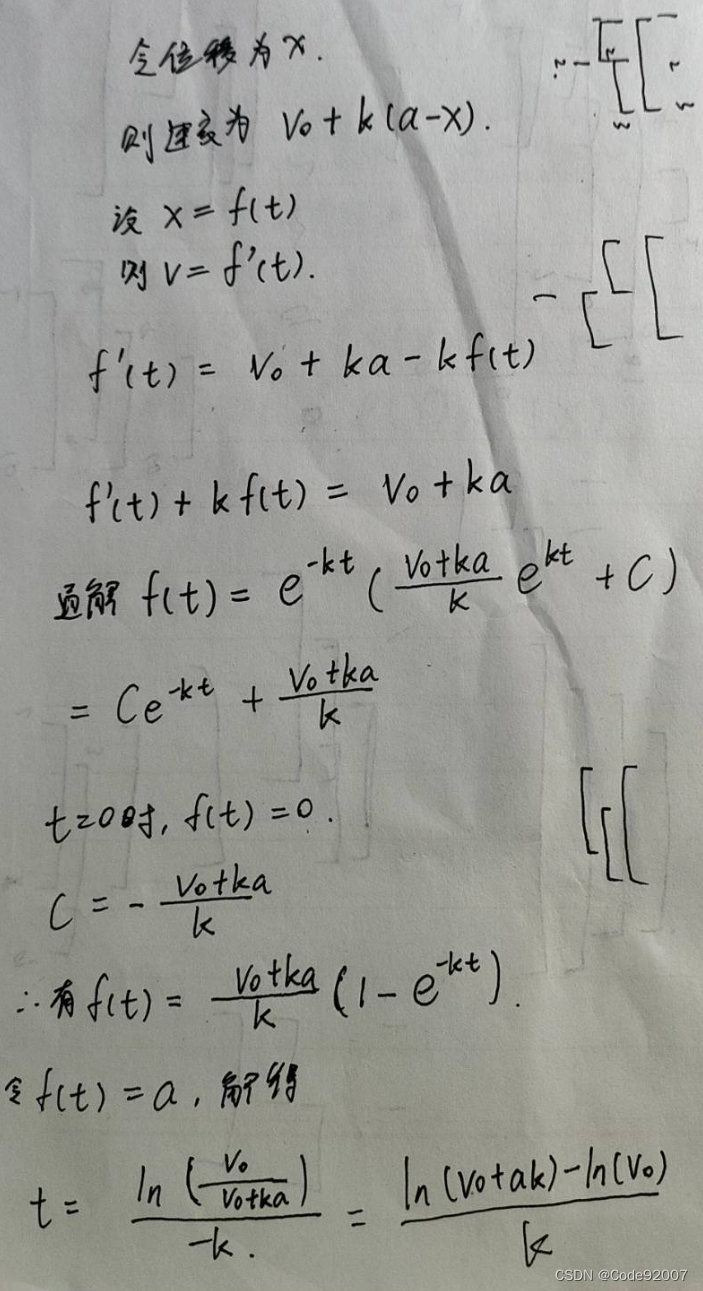
#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=1e3+5;
struct Point{
int x,y;
}p[N];
int t,n,m;
db v0,k;
ll cross(Point o,Point a,Point b){
return 1ll*(a.x-o.x)*(b.y-o.y)-1ll*(a.y-o.y)*(b.x-o.x);
}
int binary(Point *p,Point &tp){
//条件:p点集必须是顺时针或者逆时针
//(注意3点共线下的点也必须满足这个条件)
//(如果有3点共线极角序不能完成该条件)
int l=0,r=n-1;
while(l<r){
int m=(l+r)>>1;
ll c1=cross(p[0],p[m],tp);
ll c2=cross(p[0],p[(m+1)%n],tp);
ll c3=cross(p[m],p[(m+1)%n],tp);
if(c1>=0 && c2<=0 && c3>=0){
if(!c3 || (m==1 && !c1) || (m==n-2 && !c2))return 0;
return 1;
}
if(c1>=0)l=m+1;
else r=m;
}
return -1;
}
db cal(db x,db y,db x1,db y1,db x2,db y2){
db cross = (x2 - x1) * (x - x1) + (y2 - y1) * (y - y1);
if (cross <= 0)return sqrt((x - x1) * (x - x1) + (y - y1) * (y - y1));
db d2 = (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1);
if (cross >= d2)return sqrt((x - x2) * (x - x2) + (y - y2) * (y - y2));
db r = cross / d2;
db px = x1 + (x2 - x1) * r;
db py = y1 + (y2 - y1) * r;
return sqrt((x - px) * (x - px) + (y - py) * (y - py));
}
int main(){
sci(n);
rep(i,0,n-1){
sci(p[i].x),sci(p[i].y);
}
reverse(p,p+n);
p[n]=p[0];
scanf("%d%lf%lf",&m,&v0,&k);
while(m--){
Point tp;
scanf("%d%d",&tp.x,&tp.y);
int v=binary(p,tp);
if(v==1){
db s=1e18;
rep(i,0,n-1){
s=min(s,cal(tp.x,tp.y,p[i].x,p[i].y,p[i+1].x,p[i+1].y));
}
db ans;
if(k==0)ans=s/v0;
else ans=1/k*(log(v0+k*s)-log(v0));
printf("%.10lf\n",ans);
}
else if(v==0){
puts("0");
}
else{
puts("-1");
}
}
return 0;
}F. 感染的圣巢(树直径)
细节比较多,但整体还是有迹可循的
离线,倒着把点加回来,删点的树直径不会做,但是加点的树直径是好做的
每个被删的点,只需要考虑它往上到根这些点,最多60个,
把这60*2e5个点建出树来,剩下的树的部分不用建出来,只需要搜到对应的第一层就返回即可
因为只要底下的层数>=1,就一定能找到两个最远的儿子(比如找编号最小和最大的)
预处理这棵树每个点被删的时机,只需用父亲的被删时间和当前点的被删时间取min
先对n个点操作完之后剩的部分的树,求出直径的两个点
后面按删的时机倒着把点都加回来,时机相同时,加的时候按点号从小到大加
开map/unordered_map常数比较大会tle,所以只能把60*2e5个点加进01trie
懒得写了,直接抄泽与的代码
// 确认这份是 STD 了
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5 + 5;
const int M = 61 * N;
ll q[N], num[M];
int cnt, ans[N], n, m;
int son[M][2], dep[M], t[M], fa[M];
ll rd() {
ll ret = 0; char ch = getchar();
for(; isdigit(ch); ch = getchar())
ret = (ret << 1) + (ret << 3) + (ch ^ 48);
return ret;
}
void insert(ll x, int time) {
int u = 1, flag = 0;
for(int i = 59; i >= 0; i--) {
int temp = !!(x & (1LL << i));
if(flag) {
if(!son[u][temp]) {
son[u][temp] = ++cnt;
dep[cnt] = dep[u] + 1;
num[cnt] = num[u] * 2 + temp;
t[cnt] = m;
fa[cnt] = u;
}
u = son[u][temp];
}
if(temp) flag = 1;
}
t[u] = min(t[u], time);
}
int numdis(ll u, ll v) {
if(u > v) swap(u, v);
int i = 59, j = 59;
while(!(v >> j)) j--, i--;
while(!(u >> i)) i--;
while(i >= 0 && ((u >> i) & 1) == ((v >> j) & 1)) i--, j--;
return i + j + 2;
}
int dis(int u, int v) {
if(u == v) {
int ret = 0;
if(!son[u][0] && !son[u][1]) ret = max(ret, (n - dep[u]) * 2);
else if(!son[u][0] || !son[u][1]) {
ret = max(ret, (n - dep[u] - 1) * 2);
if(u == 1) ret = max(ret, n - dep[u]);
}
return ret;
}
int ret = numdis(num[u], num[v]);
if(!son[u][0] || !son[u][1]) ret += n - dep[u];
if(!son[v][0] || !son[v][1]) ret += n - dep[v];
return ret;
}
vector<int> vec[N];
int main(int argc, char *argv[]) {
// if(argc == 3) {
// freopen(argv[1] + 1, "rb", stdin);
// freopen(argv[2] + 1, "wb", stdout);
// }
n = rd(), m = rd();
dep[1] = num[1] = cnt = 1;
for(int i = 1; i < M; i++) t[i] = m;
for(int i = 1; i <= m; i++)
q[i] = rd(), insert(q[i], i - 1);
for(int i = 2; i <= cnt; i++)
t[i] = min(t[i], t[fa[i]]);
for(int i = 2; i <= cnt; i++) {
vec[t[i]].push_back(i);
}
int u = 1, v = 1, d = dis(1, 1);
for(int i = m; i > 0; i--) {
for(int w : vec[i]) {
int tu = u, tv = v, td = d, temp;
if((temp = dis(w, w)) > td) tu = w, tv = w, td = temp;
if((temp = dis(v, w)) > td) tu = v, tv = w, td = temp;
if((temp = dis(u, w)) > td) tu = u, tv = w, td = temp;
u = tu, v = tv, d = td;
}
ans[i] = d;
}
for(int i = 1; i <= m; i++) {
cout << ans[i];
if(i == m) cout << '\n';
else cout << ' ';
}
return 0;
}当然可以把求lca距离的部分改成倍增,从O(n)变成O(logn),其中n是60,因为库函数近似O(1)
int lg(ll x){
return 63-__builtin_clzll(x);
}
int dis(ll p,ll q){
int x=lg(p),y=lg(q);
if(x>y)swap(p,q),swap(x,y);
q>>=(y-x);
if(p==q)return y-x;
per(i,6,0){
int s=1<<i;
if((p>>s)^(q>>s))p>>=s,q>>=s;
}
p>>=1;
int z=lg(p);
return y-z+x-z;
}