代码随想录算法训练营第67天:图论5
105.有向图的完全可达性
卡码网题目链接(ACM模式)(opens new window)
【题目描述】
给定一个有向图,包含 N 个节点,节点编号分别为 1,2,…,N。现从 1 号节点开始,如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
【输入描述】
第一行包含两个正整数,表示节点数量 N 和边的数量 K。 后续 K 行,每行两个正整数 s 和 t,表示从 s 节点有一条边单向连接到 t 节点。
【输出描述】
如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
【输入示例】
4 4
1 2
2 1
1 3
3 4
【输出示例】
1
【提示信息】
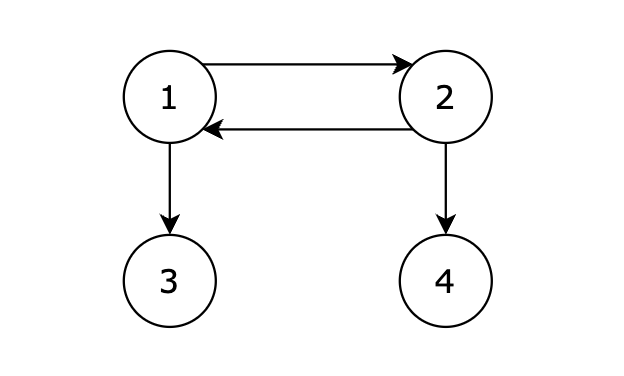
从 1 号节点可以到达任意节点,输出 1。
数据范围:
- 1 <= N <= 100;
- 1 <= K <= 2000。
#思路
本题给我们是一个有向图, 意识到这是有向图很重要!
接下来我们再画一个图,从图里可以直观看出来,节点6 是 不能到达节点1 的
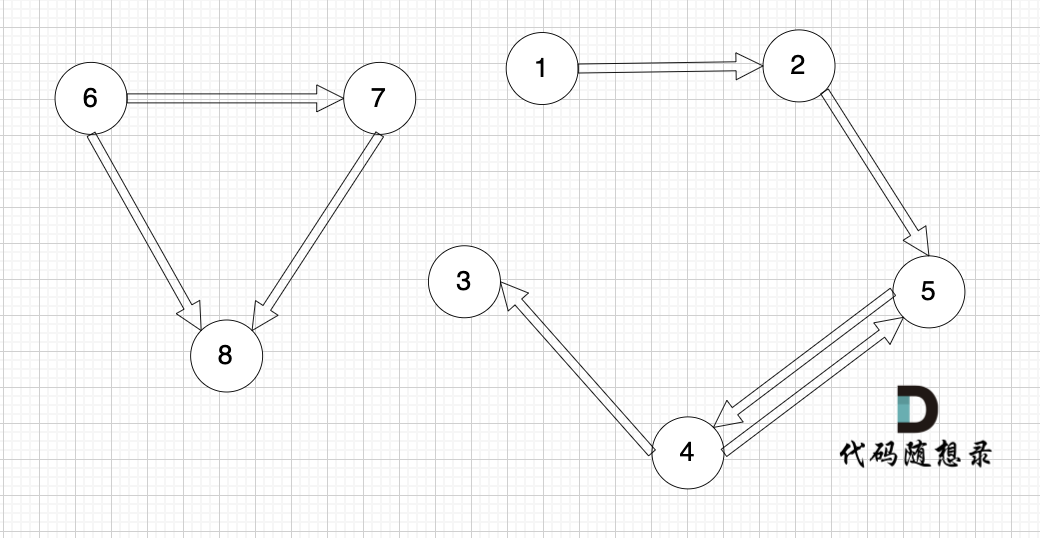
这就很容易让我们想起岛屿问题,只要发现独立的岛,就是不可到达的。
但本题是有向图,在有向图中,即使所有节点都是链接的,但依然不可能从0出发遍历所有边。
例如上图中,节点1 可以到达节点2,但节点2是不能到达节点1的。
所以本题是一个有向图搜索全路径的问题。 只能用深搜(DFS)或者广搜(BFS)来搜。
以下dfs分析 大家一定要仔细看,本题有两种dfs的解法,很多题解没有讲清楚。 看完之后 相信你对dfs会有更深的理解。
深搜三部曲:
- 确认递归函数,参数
需要传入地图,需要知道当前我们拿到的key,以至于去下一个房间。
同时还需要一个数组,用来记录我们都走过了哪些房间,这样好知道最后有没有把所有房间都遍历的,可以定义一个一维数组。
所以 递归函数参数如下:
// key 当前得到的可以
// visited 记录访问过的房间
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
- 确认终止条件
遍历的时候,什么时候终止呢?
这里有一个很重要的逻辑,就是在递归中,我们是处理当前访问的节点,还是处理下一个要访问的节点。
这决定 终止条件怎么写。
首先明确,本题中什么叫做处理,就是 visited数组来记录访问过的节点,该节点默认 数组里元素都是false,把元素标记为true就是处理 本节点了。
如果我们是处理当前访问的节点,当前访问的节点如果是 true ,说明是访问过的节点,那就终止本层递归,如果不是true,我们就把它赋值为true,因为这是我们处理本层递归的节点。
代码就是这样:
// 写法一:处理当前访问的节点
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
if (visited[key]) {
return;
}
visited[key] = true;
list<int> keys = graph[key];
for (int key : keys) {
// 深度优先搜索遍历
dfs(graph, key, visited);
}
}
如果我们是处理下一层访问的节点,而不是当前层。那么就要在 深搜三部曲中第三步:处理目前搜索节点出发的路径的时候对 节点进行处理。
这样的话,就不需要终止条件,而是在 搜索下一个节点的时候,直接判断 下一个节点是否是我们要搜的节点。
代码就是这样的:
// 写法二:处理下一个要访问的节点
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
list<int> keys = rooms[key];
for (int key : keys) {
if (visited[key] == false) { // 确认下一个是没访问过的节点
visited[key] = true;
dfs(rooms, key, visited);
}
}
}
可以看出,如何看待 我们要访问的节点,直接决定了两种不一样的写法,很多录友对这一块很模糊,可能做过这道题,但没有思考到这个维度上。
- 处理目前搜索节点出发的路径
其实在上面,深搜三部曲 第二部,就已经讲了,因为终止条件的两种写法, 直接决定了两种不一样的递归写法。
这里还有细节:
看上面两个版本的写法中, 好像没有发现回溯的逻辑。
我们都知道,有递归就有回溯,回溯就在递归函数的下面, 那么之前我们做的dfs题目,都需要回溯操作,例如:0098.所有可达路径, 为什么本题就没有回溯呢?
代码中可以看到dfs函数下面并没有回溯的操作。
此时就要在思考本题的要求了,本题是需要判断 1节点 是否能到所有节点,那么我们就没有必要回溯去撤销操作了,只要遍历过的节点一律都标记上。
那什么时候需要回溯操作呢?
当我们需要搜索一条可行路径的时候,就需要回溯操作了,因为没有回溯,就没法“调头”, 如果不理解的话,去看我写的 0098.所有可达路径 的题解。
以上分析完毕,DFS整体实现C++代码如下:
// 写法一:dfs 处理当前访问的节点
#include <iostream>
#include <vector>
#include <list>
using namespace std;
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
if (visited[key]) {
return;
}
visited[key] = true;
list<int> keys = graph[key];
for (int key : keys) {
// 深度优先搜索遍历
dfs(graph, key, visited);
}
}
int main() {
int n, m, s, t;
cin >> n >> m;
// 节点编号从1到n,所以申请 n+1 这么大的数组
vector<list<int>> graph(n + 1); // 邻接表
while (m--) {
cin >> s >> t;
// 使用邻接表 ,表示 s -> t 是相连的
graph[s].push_back(t);
}
vector<bool> visited(n + 1, false);
dfs(graph, 1, visited);
//检查是否都访问到了
for (int i = 1; i <= n; i++) {
if (visited[i] == false) {
cout << -1 << endl;
return 0;
}
}
cout << 1 << endl;
}
第二种写法注意有注释的地方是和写法一的区别
写法二:dfs处理下一个要访问的节点
#include <iostream>
#include <vector>
#include <list>
using namespace std;
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
list<int> keys = rooms[key];
for (int key : keys) {
if (visited[key] == false) { // 确认下一个是没访问过的节点
visited[key] = true;
dfs(rooms, key, visited);
}
}
}
int main() {
int n, m, s, t;
cin >> n >> m;
vector<list<int>> graph(n + 1);
while (m--) {
cin >> s >> t;
graph[s].push_back(t);
}
vector<bool> visited(n + 1, false);
visited[0] = true; // 节点1 预先处理
dfs(graph, 1, visited);
for (int i = 1; i <= n; i++) {
if (visited[i] == false) {
cout << -1 << endl;
return 0;
}
}
cout << 1 << endl;
}
本题我也给出 BFS C++代码,BFS理论基础 **(opens new window)** ,代码如下:
#include <iostream>
#include <vector>
#include <list>
#include <queue>
using namespace std;
int main() {
int n, m, s, t;
cin >> n >> m;
vector<list<int>> graph(n + 1);
while (m--) {
cin >> s >> t;
graph[s].push_back(t);
}
vector<bool> visited(n + 1, false);
visited[1] = true; // 1 号房间开始
queue<int> que;
que.push(1); // 1 号房间开始
// 广度优先搜索的过程
while (!que.empty()) {
int key = que.front(); que.pop();
list<int> keys = graph[key];
for (int key : keys) {
if (!visited[key]) {
que.push(key);
visited[key] = true;
}
}
}
for (int i = 1; i <= n; i++) {
if (visited[i] == false) {
cout << -1 << endl;
return 0;
}
}
cout << 1 << endl;
}
106. 岛屿的周长
卡码网题目链接(ACM模式)(opens new window)
题目描述
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿是被水包围,并且通过水平方向或垂直方向上相邻的陆地连接而成的。
你可以假设矩阵外均被水包围。在矩阵中恰好拥有一个岛屿,假设组成岛屿的陆地边长都为 1,请计算岛屿的周长。岛屿内部没有水域。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述
输出一个整数,表示岛屿的周长。
输入示例
5 5
0 0 0 0 0
0 1 0 1 0
0 1 1 1 0
0 1 1 1 0
0 0 0 0 0
输出示例
14
提示信息
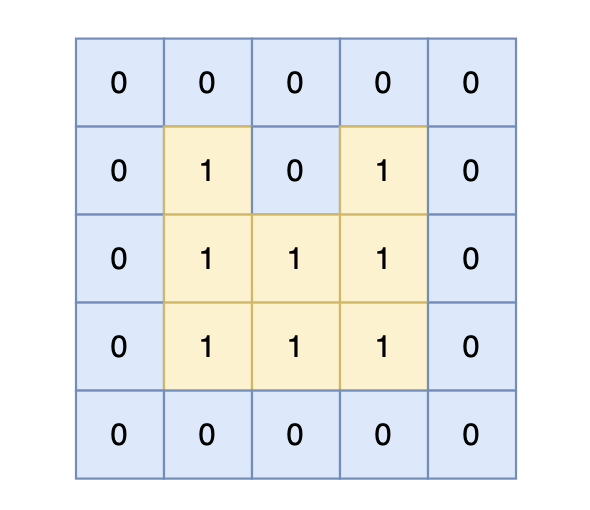
岛屿的周长为 14。
数据范围:
1 <= M, N <= 50。
#思路
岛屿问题最容易让人想到BFS或者DFS,但本题确实还用不上。
为了避免大家惯性思维,所以给大家安排了这道题目。
#解法一:
遍历每一个空格,遇到岛屿则计算其上下左右的空格情况。
如果该陆地上下左右的空格是有水域,则说明是一条边,如图:
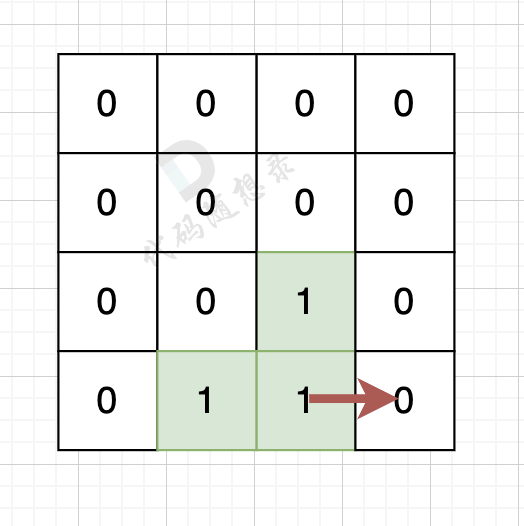
陆地的右边空格是水域,则说明找到一条边。
如果该陆地上下左右的空格出界了,则说明是一条边,如图:
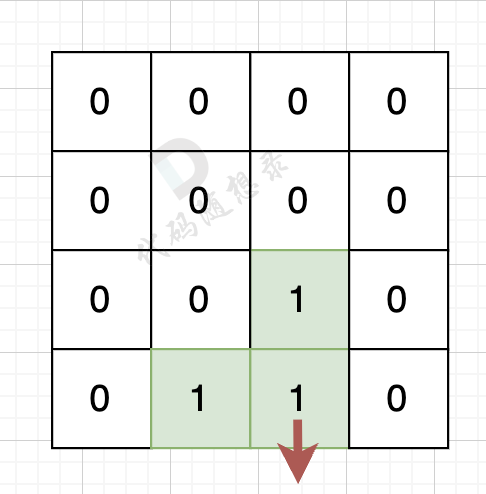
该录友的下边空格出界了,则说明找到一条边。
C++代码如下:(详细注释)
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
int direction[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) {
for (int k = 0; k < 4; k++) { // 上下左右四个方向
int x = i + direction[k][0];
int y = j + direction[k][1]; // 计算周边坐标x,y
if (x < 0 // x在边界上
|| x >= grid.size() // x在边界上
|| y < 0 // y在边界上
|| y >= grid[0].size() // y在边界上
|| grid[x][y] == 0) { // x,y位置是水域
result++;
}
}
}
}
}
cout << result << endl;
}
#解法二:
计算出总的岛屿数量,总的变数为:岛屿数量 * 4
因为有一对相邻两个陆地,边的总数就要减2,如图红线部分,有两个陆地相邻,总边数就要减2
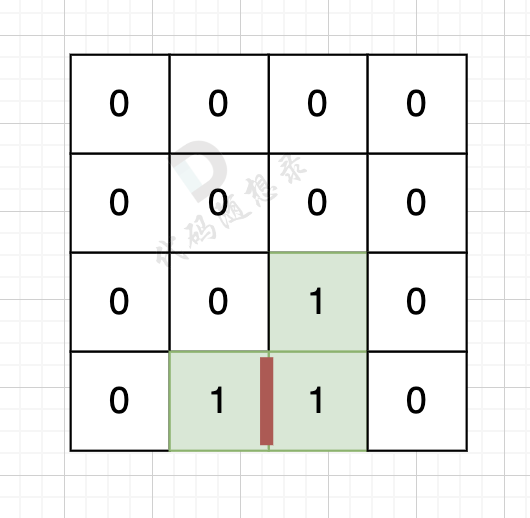
那么只需要在计算出相邻岛屿的数量就可以了,相邻岛屿数量为cover。
结果 result = 岛屿数量 * 4 - cover * 2;
C++代码如下:(详细注释)
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
int sum = 0; // 陆地数量
int cover = 0; // 相邻数量
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) {
sum++; // 统计总的陆地数量
// 统计上边相邻陆地
if(i - 1 >= 0 && grid[i - 1][j] == 1) cover++;
// 统计左边相邻陆地
if(j - 1 >= 0 && grid[i][j - 1] == 1) cover++;
// 为什么没统计下边和右边? 因为避免重复计算
}
}
}
cout << sum * 4 - cover * 2 << endl;
}







![mybatis mapper.xml 比较运算符(大于|小于|等于)的写法: 转义和<![CDATA[]]>](https://img-blog.csdnimg.cn/direct/c952487c7121458ca9cc717ae7d9d234.png)