1. 图论理论基础
1.1 图的基本概念
二维坐标中,两点可以连成线,多个点连成的线就构成了图。
当然图也可以就一个节点,甚至没有节点(空图)
1.1.1 图的种类
- 有向图
- 加权有向图
- 无权有向图
- 无向图
- 加权无向图
- 无权无向图
1.1.2 度
- 无向图的度
- 无向图中连接节点的边数等于该节点的度数
- 有向图的度
- 出度:从该节点出发的边的个数
- 入度:指向该节点边的个数
1.2 连通性
-
无向图
- 连通图
- 在无向图中,任何两个节点都是可以到达的,我们称之为连通图
- 非连通图
- 如果有节点不能到达其他节点,则为非连通图
- 连通图
-
有向图
- 强连通图
- 在有向图中,任何两个节点是可以相互到达的,我们称之为强连通图。
- 强连通图
-
连通分量
- 无向图中的极大连通子图称之为该图的一个连通分量。
-
强连通分量
- 有向图中极大强连通子图称之为该图的强连通分量
1.3 图的构造
1.3.1 邻接矩阵
邻接矩阵 使用 二维数组来表示图结构。 邻接矩阵是从节点的角度来表示图,有多少节点就申请多大的二维数组。
- 邻接矩阵的优点:
- 表达方式简单,易于理解
- 检查任意两个顶点间是否存在边的操作非常快
- 适合稠密图,在边数接近顶点数平方的图中,邻接矩阵是一种空间效率较高的表示方法。
- 缺点:
- 遇到稀疏图,会导致申请过大的二维数组造成空间浪费且遍历边的时候需要遍历整个n * n矩阵,造成时间浪费
1.3.2 邻接表
邻接表使用数组 + 链表的方式来表示。 邻接表是从边的数量来表示图,有多少边才会申请对应大小的链表。
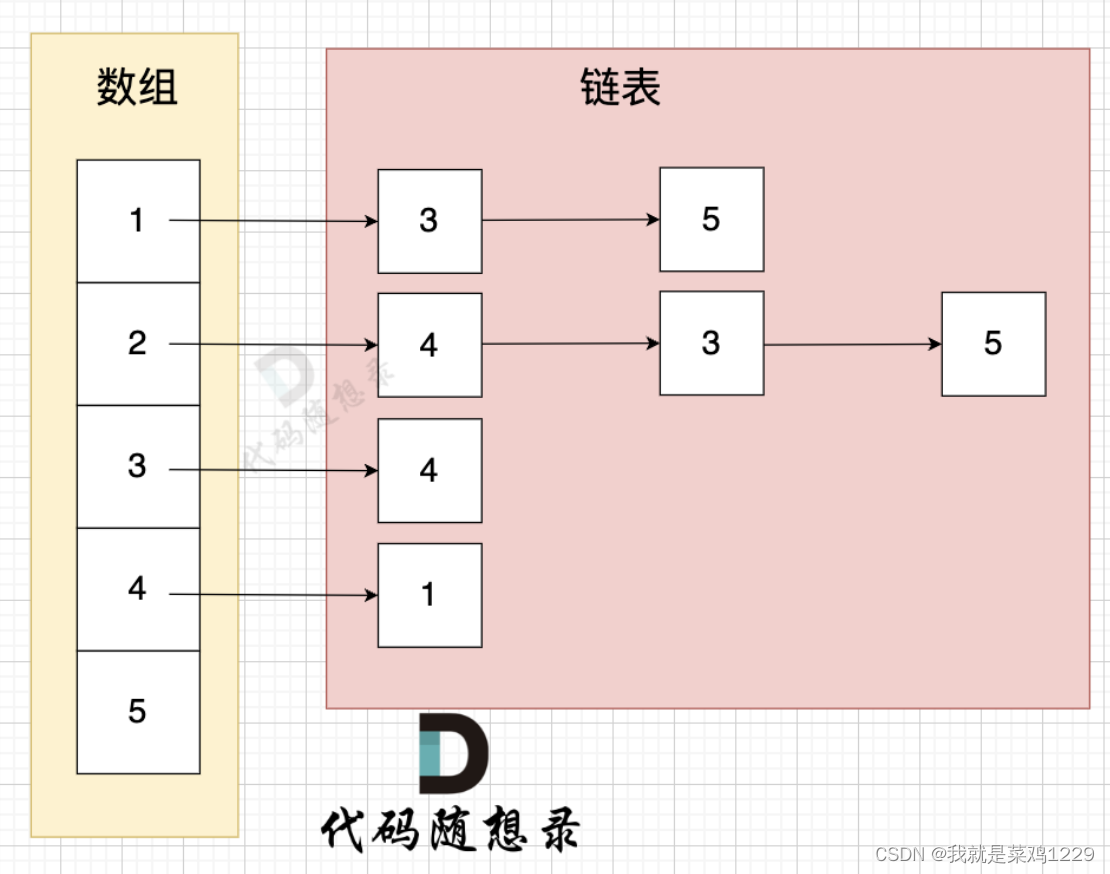
- 邻接表的优点:
- 对于稀疏图的存储,只需要存储边,空间利用率高
- 遍历节点连接情况相对容易
- 缺点:
- 检查任意两个节点间是否存在边,效率相对低,需要 O(V)时间,V表示某节点连接其他节点的数量。
- 实现相对复杂,不易理解
1.4 图的遍历方式
- 深度优先搜索(dfs)
- dfs是可一个方向去搜,不到黄河不回头,直到遇到绝境了,搜不下去了,再换方向(换方向的过程就涉及到了回溯)。
- 广度优先搜索(bfs)
- bfs是先把本节点所连接的所有节点遍历一遍,走到下一个节点的时候,再把连接节点的所有节点遍历一遍,搜索方向更像是广度,四面八方的搜索过程。
2. 深度优先搜索理论基础
2.1 代码模板
深度优先搜索策略一般上使用递归的方式来实现。
// 递归模板
void dfs(参数){
处理节点
dfs(图,选择的节点)//递归
回溯,撤销处理结果
}
// 回溯法的代码框架
void backtracking(参数){
if (终止条件){
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就上集合的大小)){
处理节点;
backtracking(路径,选择列表);
回溯,撤销处理结果
}
}
//其实回溯代码的过程就上一个dfs的过程
void dfs(参数){
if(终止条件){
存放结果;
return;
}
for (选择:本节点所连接的其他节点){
处理节点;
dfs(图,选择的节点);//递归
回溯,撤销处理结果
}
}
2.2 深搜三部曲
-
确认递归函数,参数
一般情况,深搜需要 二维数组数组结构保存所有路径,需要一维数组保存单一路径,这种保存结果的数组,我们可以定义一个全局变量,避免让我们的函数参数过多。vector<vector<int>> result; // 保存符合条件的所有路径 vector<int> path; // 起点到终点的路径 void dfs (图,目前搜索的节点) -
确认终止条件
if (终止条件) { 存放结果; return; } -
处理目前搜索节点出发的路径
for (选择:本节点所连接的其他节点) { 处理节点; dfs(图,选择的节点); // 递归 回溯,撤销处理结果 }
3. 广度优先搜索理论基础
- 广搜的搜索方式就适合于解决两个点之间的最短路径问题。
- 因为广搜是从起点出发,以起始点为中心一圈一圈进行搜索,一旦遇到终点,记录之前走过的节点就是一条最短路。
- 广度搜索需要的仅仅需要一个容器,用来保存我们要遍历的元素即可
代码模板如下
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
// grid 是地图,也就是一个二维数组
// visited标记访问过的节点,不要重复访问
// x,y 表示开始搜索节点的下标
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que; // 定义队列
que.push({x, y}); // 起始节点加入队列
visited[x][y] = true; // 只要加入队列,立刻标记为访问过的节点
while(!que.empty()) { // 开始遍历队列里的元素
pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素
int curx = cur.first;
int cury = cur.second; // 当前节点坐标
for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1]; // 获取周边四个方向的坐标
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 坐标越界了,直接跳过
if (!visited[nextx][nexty]) { // 如果节点没被访问过
que.push({nextx, nexty}); // 队列添加该节点为下一轮要遍历的节点
visited[nextx][nexty] = true; // 只要加入队列立刻标记,避免重复访问
}
}
}
}
4. 所有可达路径
4.1 dfs邻接矩阵版本
package main
import "fmt"
// 地图数据
var m [][]int
// 结果
var result [][]int
// 路径
var path []int
func main() {
var N, M int
_, err := fmt.Scanln(&N, &M)
if err != nil {
fmt.Println(2001)
return
}
// 使用邻接矩阵存储地图信息
m = make([][]int, N+1)
for i := 0; i <= N; i++ {
m[i] = make([]int, N+1)
}
var from, to int
for i := 0; i < M; i++ {
_, err := fmt.Scanln(&from, &to)
if err != nil {
fmt.Println(2002)
return
}
m[from][to] = 1
}
//初始化变量
result = make([][]int, 0)
path = make([]int, 0)
//dfs递归
path = append(path, 1)
dfs(1, N)
// 输出结果
if len(result) == 0 {
fmt.Println(-1)
} else {
printMatrix(result)
}
}
func dfs(now int, end int) {
//终止条件
if now == end {
temp := make([]int, len(path))
copy(temp, path)
result = append(result, temp)
return
}
//遍历
for i := 1; i < len(m); i++ {
if m[now][i] == 1 {
path = append(path, i)
dfs(i, end)
path = path[:len(path)-1]
}
}
}
func printMatrix(matrix [][]int) {
for i := 0; i < len(matrix); i++ {
printArray(matrix[i])
}
}
func printArray(arr []int) {
for i := 0; i < len(arr); i++ {
if i == 0 {
fmt.Print(arr[i])
} else {
fmt.Printf(" %d", arr[i])
}
}
fmt.Println()
}
4.2 dfs邻接表版本
package main
import "fmt"
// 地图数据
var m [][]int
// 结果
var result [][]int
// 路径
var path []int
func main() {
var N, M int
_, err := fmt.Scanln(&N, &M)
if err != nil {
fmt.Println(2001)
return
}
// 使用邻接表存储地图信息
m = make([][]int, N+1)
for i := 0; i <= N; i++ {
m[i] = make([]int, 0)
}
var from, to int
for i := 0; i < M; i++ {
_, err := fmt.Scanln(&from, &to)
if err != nil {
fmt.Println(2002)
return
}
m[from] = append(m[from], to)
}
//初始化变量
result = make([][]int, 0)
path = make([]int, 0)
//dfs递归
path = append(path, 1)
dfs(1, N)
// 输出结果
if len(result) == 0 {
fmt.Println(-1)
} else {
printMatrix(result)
}
}
func dfs(now int, end int) {
//终止条件
if now == end {
temp := make([]int, len(path))
copy(temp, path)
result = append(result, temp)
return
}
//遍历
for i := 0; i < len(m[now]); i++ {
path = append(path, m[now][i])
dfs(m[now][i], end)
path = path[:len(path)-1]
}
}
func printMatrix(matrix [][]int) {
for i := 0; i < len(matrix); i++ {
printArray(matrix[i])
}
}
func printArray(arr []int) {
for i := 0; i < len(arr); i++ {
if i == 0 {
fmt.Print(arr[i])
} else {
fmt.Printf(" %d", arr[i])
}
}
fmt.Println()
}
4.4 结果分析

上面的是邻接表跑出来的结果,下面是邻接矩阵跑出来的结果。
相差不大只能说。(应该是测试用例的问题)