使用 PCA 可视化数据的分类能力

news2024/10/5 16:23:24

使用 PCA 探索数据分类的效果（使用 Python 代码）

「AI秘籍」系列课程：

人工智能应用数学基础
人工智能Python基础
人工智能基础核心知识
人工智能BI核心知识
人工智能CV核心知识

主成分分析 (PCA) 是数据科学家使用的绝佳工具。它可用于降低特征空间维数并生成不相关的特征。正如我们将看到的，它还可以帮助你深入了解数据的分类能力。我们将带你了解如何以这种方式使用 PCA。提供了 Python 代码片段，完整项目可在GitHub¹上找到。

什么是 PCA？

我们先从理论开始。我不会深入讲解太多细节，因为如果你想了解 PCA 的工作原理，有很多很好的资源^2^3。重要的是要知道 PCA 是一种降维算法。这意味着它用于减少用于训练模型的特征数量。它通过从许多特征中构建主成分 (PC) 来实现这一点。

PC 的构造方式是，第一个 PC（即 PC1）尽可能解释特征中的大部分变化。然后 PC2 尽可能解释剩余变化中的大部分变化，依此类推。PC1 和 PC2 通常可以解释总特征变化的很大一部分。另一种思考方式是，前两个 PC 可以很好地总结特征。这很重要，因为它使我们能够在二维平面上直观地看到数据的分类能力。

数据集

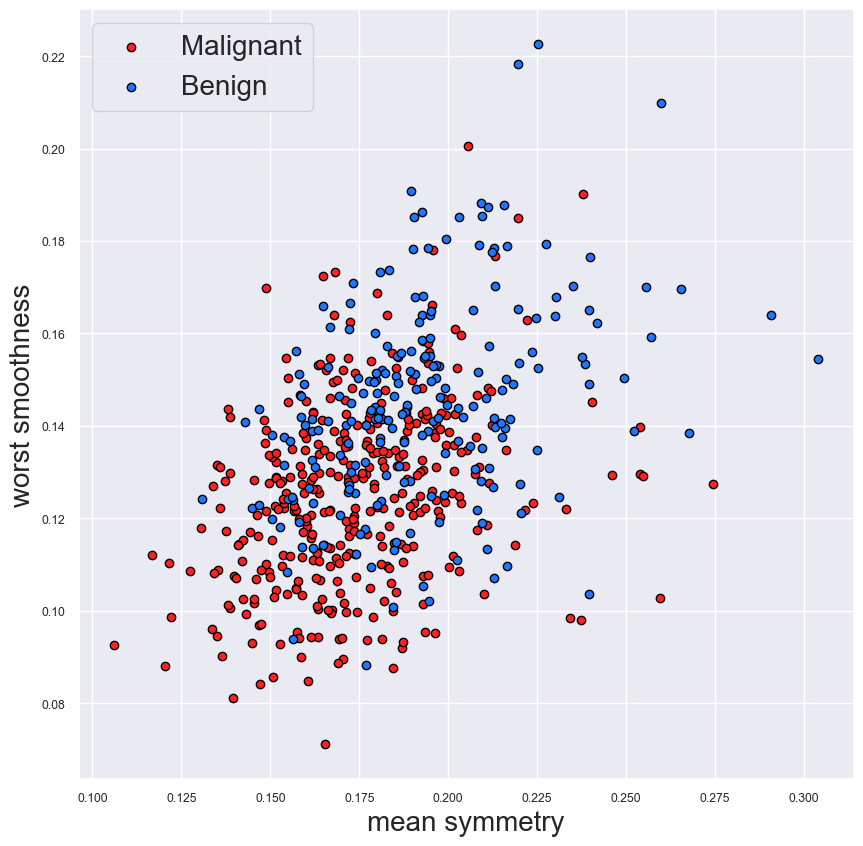
好的，让我们深入研究一个实际的例子。我们将使用 PCA 来探索乳腺癌数据集^4，我们使用以下代码导入该数据集。目标变量是乳腺癌测试的结果 - 恶性或良性。每次测试都会取出许多癌细胞。然后从每个癌细胞中采取 10 个不同的测量值。这些包括细胞半径和细胞对称性等测量值。为了获得 30 个特征的最终列表，我们以 3 种方式汇总这些测量值。也就是说，我们计算每个测量值的平均值、标准误差和最大值（“最差”值）。在图 1 中，我们仔细研究了其中两个特征 -细胞的平均对称性和最差平滑度。

import numpy as np
import pandas as pd
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()

data = pd.DataFrame(cancer['data'],columns=cancer['feature_names'])
data['y'] = cancer['target']

在图 1 中，我们可以看到这两个特征有助于区分这两个类别。也就是说，良性肿瘤往往更对称、更光滑。重叠部分仍然很多，因此仅使用这些特征的模型效果不会很好。我们可以创建这样的图表来了解每个单独特征的预测能力。尽管有 30 个特征，但需要分析的图表还是很多。它们也没有告诉我们整个数据集的预测能力。这就是 PCA 发挥作用的地方。

图 1：使用两个特征的散点图

PCA——整个数据集

让我们首先对整个数据集进行 PCA。我们使用下面的代码来执行此操作。我们首先缩放特征，使它们都具有均值为 0 和方差为 1。这很重要，因为 PCA 通过最大化 PC 解释的方差来工作。由于其规模，某些特征往往会具有更高的方差。例如，以厘米为单位测量的距离的方差将高于以公里为单位测量的相同距离。如果不进行缩放，PCA 将被那些方差较大的特征“压倒”。

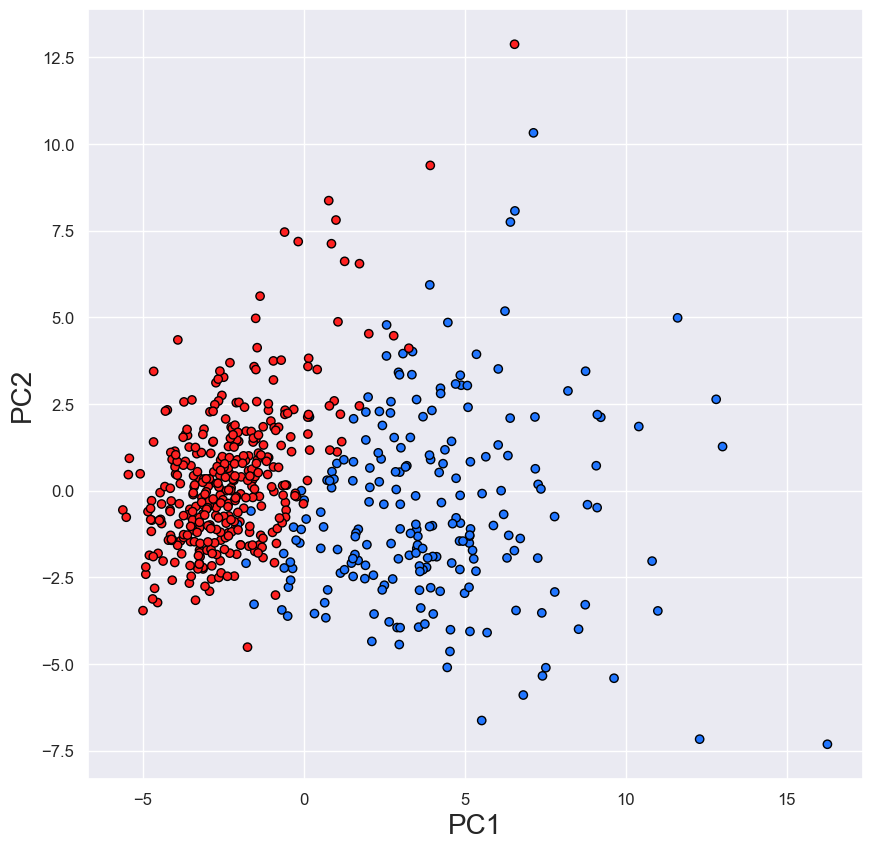
缩放完成后，我们拟合 PCA 模型并将特征转换为 PC。由于我们有 30 个特征，因此最多可以有 30 个 PC。对于我们的可视化，我们只对前两个感兴趣。你可以在图 2 中看到这一点，其中使用 PC1 和 PC2 创建了散点图。我们现在可以看到两个不同的集群，它们比图 1 中更清晰。

from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

#Scale the data
scaler = StandardScaler()
scaler.fit(data)
scaled = scaler.transform(data)

#Obtain principal components
pca = PCA().fit(scaled)

pc = pca.transform(scaled)
pc1 = pc[:,0]
pc2 = pc[:,1]

#Plot principal components
plt.figure(figsize=(10,10))

colour = ['#ff2121' if y == 1 else '#2176ff' for y in data['y']]
plt.scatter(pc1,pc2 ,c=colour,edgecolors='#000000')
plt.ylabel("Glucose",size=20)
plt.xlabel('Age',size=20)
plt.yticks(size=12)
plt.xticks(size=12)
plt.xlabel('PC1')
plt.ylabel('PC2')

该图可用于直观地了解数据的预测强度。在本例中，它表明使用整个数据集将使我们能够区分恶性肿瘤和良性肿瘤。但是，仍然有一些异常值（即不明确位于群集中的点）。这并不意味着我们会对这些情况做出错误的预测。我们应该记住，并非所有特征方差都会在前两个 PC 中捕获。在完整特征集上训练的模型可以产生更好的预测。

图 2：使用所有特征的 PCA 散点图

此时，我们应该提到这种方法的一个注意事项。PC1 和 PC2 可以解释特征中很大一部分方差。然而，这并不总是正确的。在某些情况下，PC 可能被认为是特征的糟糕总结。这意味着，即使你的数据可以很好地分离类别，你也可能无法获得清晰的聚类，如图 2 所示。

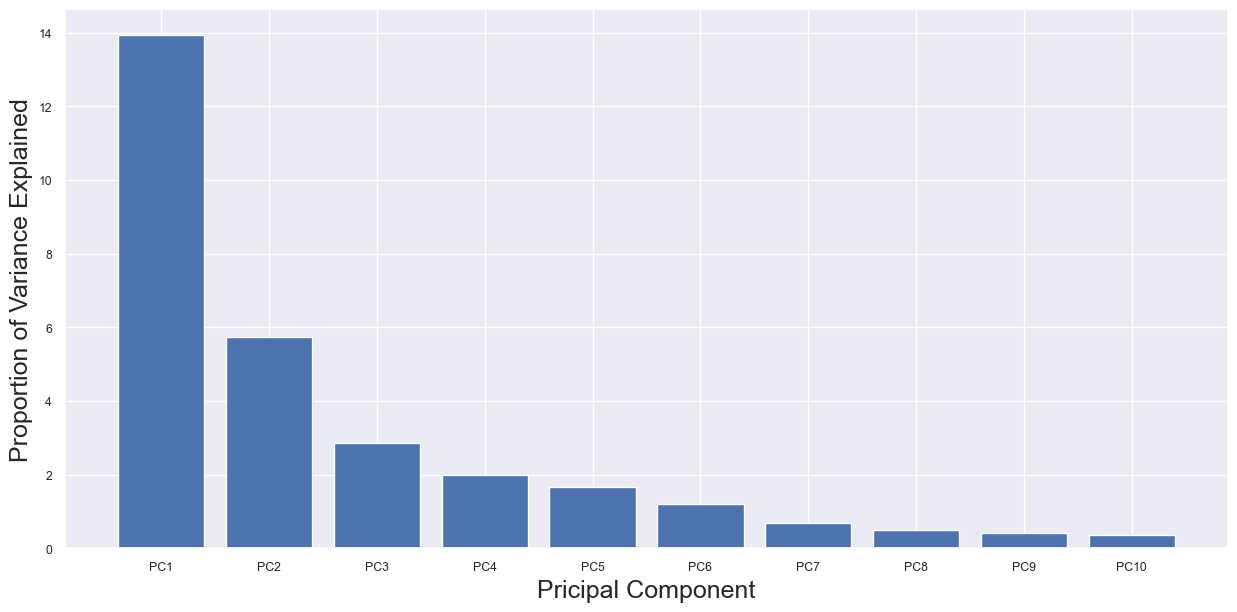
我们可以使用 PCA 碎石图来确定这是否会是一个问题。我们使用下面的代码创建了此分析的碎石图，如图 3 所示。这是一个条形图，其中每个条形的高度是相关 PC 解释的方差百分比。我们看到，PC1 和 PC2 总共只解释了约 20% 的特征方差。即使只有 20% 的解释，我们仍然得到两个不同的聚类。这强调了数据的预测强度。

var = pca.explained_variance_[0:10] #percentage of variance explained
labels = ['PC1','PC2','PC3','PC4','PC5','PC6','PC7','PC8','PC9','PC10']

plt.figure(figsize=(15,7))
plt.bar(labels,var,)
plt.xlabel('Pricipal Component')
plt.ylabel('Proportion of Variance Explained')

图 3. 碎石图
在这里插入图片描述

PCA——特征组

我们还可以使用此过程来比较不同的特征组。例如，假设我们有两组特征。第 1 组具有基于细胞对称性和平滑度特征的所有特征。而第 2 组具有基于周长和凹度的所有特征。我们可以使用 PCA 来直观地了解哪组更适合进行预测。

group_1 = ['mean symmetry', 'symmetry error','worst symmetry',
'mean smoothness','smoothness error','worst smoothness']
        
group_2 = ['mean perimeter','perimeter error','worst perimeter', 
'mean concavity','concavity error','worst concavity']

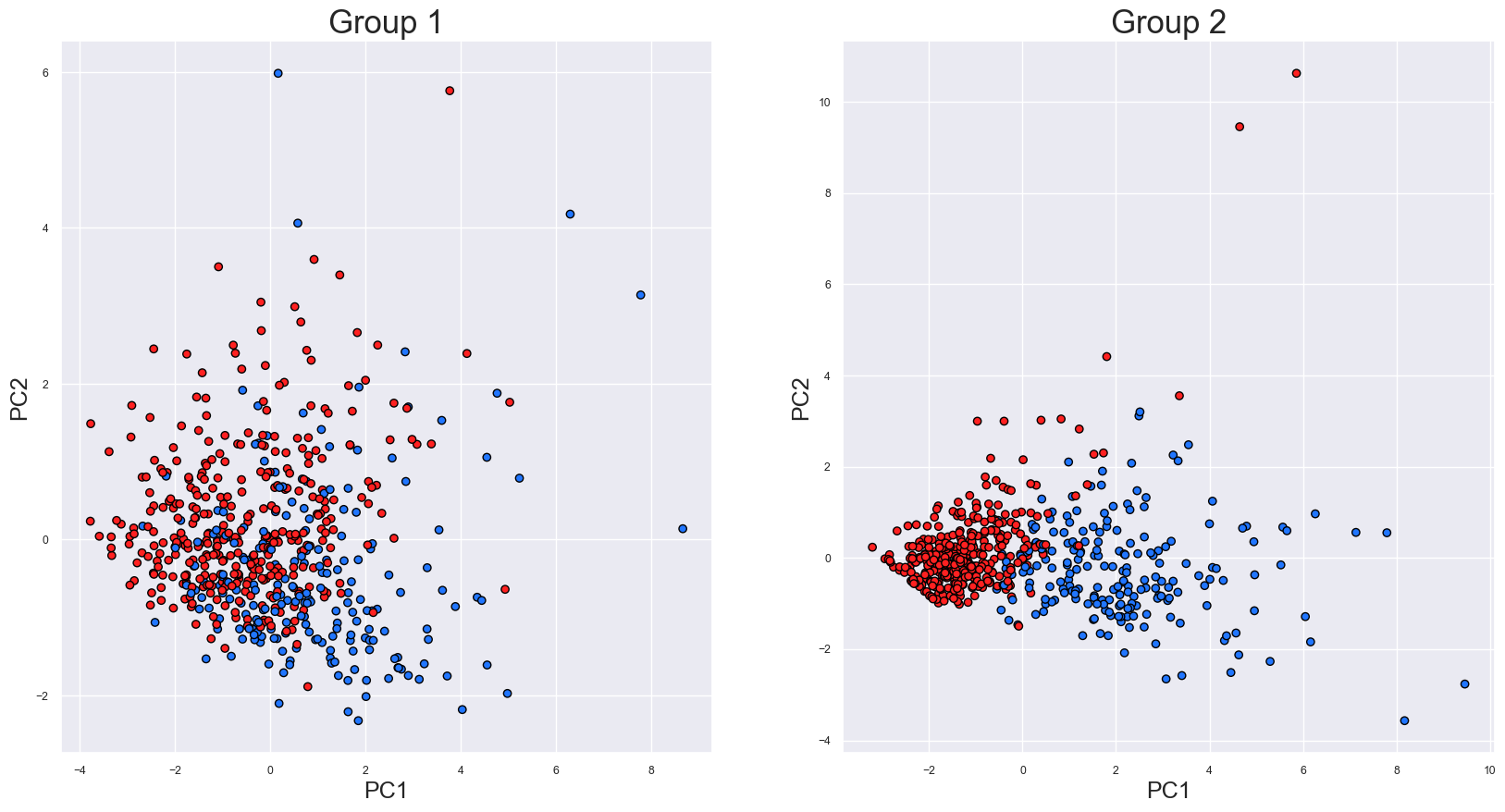
我们首先创建两组特征。然后分别对每组进行 PCA。这将为我们提供两组 PC，我们选择 PC1 和 PC2 来代表每个特征组。该过程的结果可以在图 4 中看到。

对于第 1 组，我们可以看到有一些分离，但仍然有很多重叠。相比之下，第 2 组有两个不同的簇。因此，从这些图中，我们预计第 2 组中的特征是更好的预测因子。使用第 2 组特征训练的模型应该比使用第 1 组特征训练的模型具有更高的准确率。现在，让我们来测试一下这个假设。

图 4：使用特征组的 PCA 散点图

我们使用下面的代码来训练使用两组特征的逻辑回归模型。在每种情况下，我们使用 70% 的数据来训练模型，其余 30% 的数据来测试模型。第 1 组的测试集准确率为 74%，相比之下，第 2 组的准确率为 97%。因此，第 2 组中的特征是更好的预测因子，这正是我们从 PCA 结果中预期的。

from sklearn.model_selection import train_test_split
import sklearn.metrics as metric
import statsmodels.api as sm

for i,g in enumerate(group):

    x = data[g]
    x = sm.add_constant(x)
    y = data['y']
    x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=0.3, 
                                                        random_state = 101)

    model = sm.Logit(y_train,x_train).fit() #fit logistic regression model

    predictions = np.around(model.predict(x_test)) 
    accuracy = metric.accuracy_score(y_test,predictions)
    
    print("Accuracy of Group {}: {}".format(i+1,accuracy))

---
Optimization terminated successfully.
         Current function value: 0.458884
         Iterations 7
Accuracy of Group 1: 0.7368421052631579
Optimization terminated successfully.
         Current function value: 0.103458
         Iterations 10
Accuracy of Group 2: 0.9707602339181286