基于惯性加权PSO优化的目标函数最小值求解matlab仿真

news2024/10/6 6:27:59

1.程序功能描述

2.测试软件版本以及运行结果展示

3.核心程序

4.本算法原理

5.完整程序

1.程序功能描述

基于惯性加权PSO优化的目标函数最小值求解matlab仿真。

2.测试软件版本以及运行结果展示

MATLAB2022A版本运行

（完整程序运行后无水印）

3.核心程序

..........................................................
yfits     = []; 
% 主循环开始
for iter =1: Miter
    yfit = zeros(Npop,1);  % 初始化函数值数组
    
    % 更新粒子速度
    v_pxy = func_update_V(w,v_pxy,c1,Pxy_Gbest,dt,x_pxy,c2,PL_best);
    
    % 限制速度
    v_pxy = func_rest(x_pxy,v_pxy,Vmax);
    
    % 更新位置
    x_pxy = func_update_pxy(x_pxy,v_pxy,dt);
    
    % 降低惯性权重w的影响
    if w > wMin
       w = w * beta;
    end
    
    yfits     = [yfits,V_Gbest]; 
end

Pxy_Gbest

figure;
plot(yfits);
xlabel('迭代次数');
ylabel('适应度值');


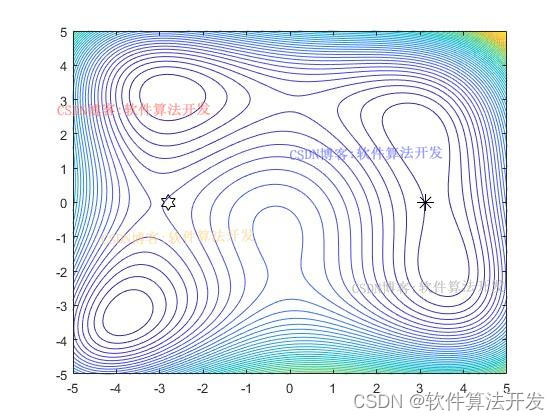
% 绘制等高线图
a = 0.01;
x1 = linspace(-5,5,1000);
x2 = x1.';
x3 = (((x1.^2)+x2-11).^2 + (x1+(x2.^2)-7).^2);


figure;
contour(x1,x2,x3,50)    
hold on
plot(Pxy_Gbest(1),V_Gbest,'kh','MarkerSize', 12) 
plot(Pxy_Gbest(2),V_Gbest,'k*','MarkerSize', 12)
63

4.本算法原理

粒子群优化（Particle Swarm Optimization, PSO）是一种启发式优化算法，最初由Eberhart和Kennedy于1995年提出，广泛应用于解决连续或离散的优化问题。惯性加权PSO（Inertia Weighted Particle Swarm Optimization, IWPSO）是对基本PSO算法的一种改进，旨在通过引入惯性权重因子来平衡算法的全局探索和局部开发能力。

PSO算法模拟鸟群觅食行为，通过一群称为“粒子”的个体在解空间中搜索最优解。每个粒子的位置xi=(xi1,xi2,...,xid)代表解空间的一个潜在解，速度vi=(vi1,vi2,...,vid)决定粒子移动的方向和速度。算法迭代更新每个粒子的位置和速度直到满足停止准则。