day01-切片和索引
ndarray对象的内容可以通过索引或切片来访问和修改,与 Python 中list 的切片操作一样。
ndarray数组可以基于0-n的下标进行索引
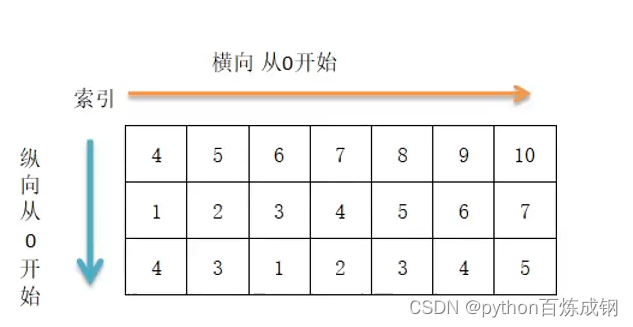
- 注意,数组切片并不像列表切片会重新开辟一片空间,而是地址引用,需要使用.copy()进行复制。
array = np.array([0,1,2,3,4,5,6,7,8,9])
ar1 = array[2:7:2]
#ar1为array([2,4,6])

特点:左闭右开【 } 用法同列表切片
多维切片
ar4 = array([[0,1,2,3],
[4,5,6,7],
[8,9,10,11],
[12,13,14,15]])
ar4.ndim
#返回ar4的秩(几维)输出2
ar4[2]
#切片为下一维度的一个元素,所以是一维数组
#输出array([8,9,10,11])
ar4[2][2]
#输出10
ar4[2:]
#输出第2行以后的
array([[8,9,10,11],
[12,13,14,15]])
- 切片还可以用省略号表示"…",如果在行位置使用省略号,那么返回值将包含所有行元素,反之,则包含所有列元素
ar4[...,1]
#取第一列1,5,9,13
ar4[...,1:]
#返回第二列后的所有项
"""
1,2,3
5,6,7
9,10,11
13,14,15
"""
#注意
ar4[1,2]
ar4[1][2]
#一个是切片一个是取索引
ar4[...][1]
#取了所有行再取第二行
#区别于
ar4[...,1]
获取四个脚上的元素组成2*2
b = np.array([[0,1,2],
[3,4,5],
[6,7,8],
[9,10,11]
])
a = b[[0,0,3,3],[0,2,0,2]] #取b[0][0],b[0][2],b[3][0],b[3][2]组成数列即b【【行号集】【列号集】】
r = np.array([[0,0],[3,3]]).reshape(4)
l = np.array([[0,2],[0,2]]).reshape(4)
s = b[r,l].reshape((2,2))
s
a = np.array([
[1,2,3],
[4,5,6],
[7,8,9],
])
#行取得2行和3行,列取得2列和3列
b = a[1:3,1:3] #等价于b = a[[1,2],[1,2]]
#1:3 == [1,2]
c = a[1:3,[1,2]]
#...表示所有行,1:表示从第二列开始的所有列
d = a[...,1:]
print(b)
print(c)
print(d)
创建一个下图的数列

z = np.zero((8,8),dtype = int)
z[1::2,::2] = 1
z[::2,1::2] = 1
z
2.布尔数组索引
当输出的结果需要经过布尔运算(如比较运算)时,此时回事用到另一种高级索引方式,即布尔数组索引
返回数组中大于6的所有元素
x = np.array([[0,1,2],[3,4,5],[6,7,8],[9,10,11]])
x[x>6]
#array([7,8,9,10,11])
联系
1.提取所有奇数
2.将奇数值修改为-1
x = np.array([[0,1,2],[3,4,5],[6,7,8],[9,10,11]])
x[x%2==1]
x[x%2==1] = -1
筛选出指定区间的数据
- & 和
- | 或
x = np.array([[0,1,2],[3,4,5],[6,7,8],[9,10,11]])
#以上x中大于4并且大于9的所有元素
x[(x<4)&(x<9)]
#以上x中大于4或者大于9的所有元素
x[(x<4)|(x<9)]
True和False的形式表示需要和不需要的数据
a = np.array(12).reshape((3,4))
array([ [0,1,2,3],
[4,5,6,7],
[8,9,10,11]
])
row1 = np.array([False,True,True])
a[row1] #第一行不要,第二行要,第三行要
#相当于 a[[1,2],:]
得到:
array([ [4,5,6,7],
[8,9,10,11]
])
column = np.array([True,False,True,False])
a[:,column]
#相当于 a[:,[0,2]]
得到:
array([ [0,4,8],
[2,6,10]
])
a[row1,column]
#a[[False,True,True],[True,False,True,False]]
#注意前后的帧需要一样,True的个数需要保持一致,不一致会报错
#等价于:
a[[1,2],[0,1]]
当需要选择的行数和列数不一致时,如选择第一行和最后一行的1,3,4列
a[[0,-1],[0,2,3]]
上述方法错误!形状不一样
1.先选行再选列,即先读取数组a的第一列和最后一列,保存到temp中然后再筛选相应的列即可
#第一步:先选行
temp = a[[0,-1],:]
#第二部再选列
temp[:,[0,2,3]]
#合并一条
a[[0,-1],:][:,[0,2,3]]
一行和最后一行的1,3,4列
a[[0,-1],[0,2,3]]
上述方法错误!形状不一样
1.先选行再选列,即先读取数组a的第一列和最后一列,保存到temp中然后再筛选相应的列即可
#第一步:先选行
temp = a[[0,-1],:]
#第二部再选列
temp[:,[0,2,3]]
#合并一条
a[[0,-1],:][:,[0,2,3]]