上回书说到数字信号处理中基本的一个通用模型框架图。今天咱们继续,可以说今天要讲的东西必须是学习数字信号处理必备的观念——模拟与数字,连续和离散。
时域离散序列
由于数字信号基本都来自模拟信号,所以先来谈谈模拟信号。模拟信号就是常说的连续时域信号,在时间上和幅度上都是连续的,也就是在任何的时刻其都是有值的且值有意义。像日常生活中就有很多连续信号的例子,有温度、压力、水位、化学浓度、电压与电流、位置、速度、加速度、力与扭矩等。如果信号仅在离散时间点上取值有效,这样的信号被称为时域离散信号,也称离散时间信号,用x(n)表示,其中变量n是整数值并在时间上代表一些离散时刻,在咱们的MATLAB里面其实简单的一维数组近似就能看成一个离散时间序列。产生离散时间序列的方法,就是采样。举个例子:xₐ=sin(t)表示一个正弦信号,它也是一个连续时间信号。如果对这个信号每隔tₐ时间间隔取一个样点,可表示成x(n)=xₐ(t)|ₜ₌ₙₜₐ=sin(ntₐ)。
接下来,介绍一下一些基本的序列。
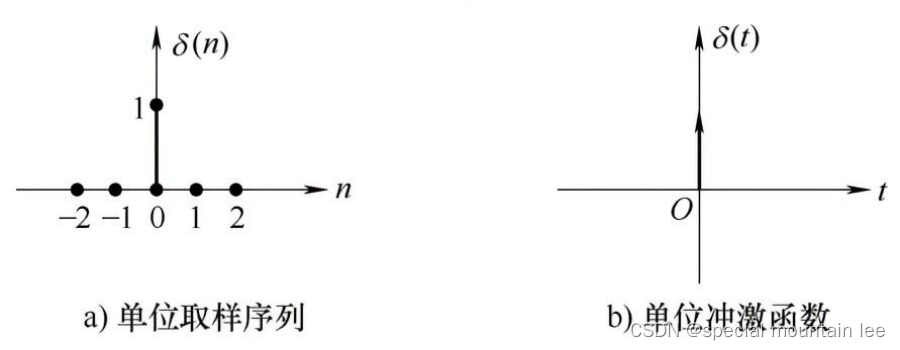
单位取样序列δ(n)是最简单也是使用最多的序列之一,仅在n=0时,其值为1,其他各值均为0。它类似于模拟信号中的单位冲激函数δ(t),不同的是δ(t)在t=0时,取值无穷大。单位取样序列和单位冲激函数如图所示。
单位阶跃序列u(n)在n≥0时,其值为1;在n<0时,其值为0。和阶跃函数差不多。阶跃函数和冲激函数的关系——u(t)求导是δ(t);映射到离散当中,微分对应的是差分,所以二者关系可以如下图概括。

至于其他的就简单说一下,像矩形序列Rɴ(n)实际上就跟门函数差不多,也可以写成
u(n)-u(n-N),或者是冲激序列的叠加。还有正余弦序列、指数序列这些就不多说了。这里值得大家注意的是所有的序列都能表示成冲激序列的线性组合,而在连续当中,我们绝大多数的情况下用的则是阶梯信号做的近似,实际上两者的意思差不多。满足等式x(n)=x(n+N)(N为正整数)的序列称为周期序列。用这个条件来检验离散时间余弦(或正弦)序列的周期性,即Acos(ωₒn+φ)=Acos[ωₒ(n+N)+φ],不难求出ωₒN=2πk,式中k为整数,也可写成N=2πk/ωₒ,下面讨论N的几种可能情况:周期序列通常分成三种不同的序列。1、当2π/ωₒ为整数时,k=1,则2π/ωₒ即为正弦序列的周期。2、当2π/ωₒ为非整数,但它是一个有理数时,设2π/ωₒ=M/N,其中M和N是互为素数的整数,这时,取k=M,则M为正弦序列的周期。3、当2π/ωₒ为无理数时,此正弦序列为非周期序列。
序列的运算
(一)信号相加
两个信号相加要求长度必须相同。如果两个序列长度不同或者长度相同,但是样本位置不同,也不能相加。可将序列增加若干零值延长,使得序列长度相等且样本位置一致。
(二)信号相乘
信号相乘即两个信号位置相同处的数值相乘,原理与信号相加类似,这里不再举例说明。
(三)信号移位
序列y(n)与x(n)的关系表示为y(n)=x(n-k),其中k为整数。当k>0时,表示序列y(n)是将x(n)向右平移k个单位的结果;当k<0时,表示序列y(n)是将x(n)向左平移k个单位的结果。
(四)信号尺度变换
信号y(n)与x(n)的关系用公式y(n)=x(mn)表示,其中m取整数,表示每隔m单位取一个样本。当然啦,如果说m<0的话,我们就应该要经历反褶这个操作,先后顺序无所谓,全看个人习惯。我一般都是先反褶,在尺度变换。
离散时间系统
说完了离散时间序列,接下来看看离散时间系统,我们通常用T[.]来表示系统函数,输入信号用x(n)表示,输出信号用y(n)表示,它们之间的关系可描述为y(n)=T[x(n)]。
一、线性系统
若某个系统的输入信号和输出信号分别用x1(n)和y1(n)来表示,它们之间的关系描述成y1(n)=T[x1(n)]。同理,该系统的输入信号为x2(n)时,输出信号可表示成y2(n)=T[x2(n)],输入信号为ax1(n)+bx2(n)时,输出信号可表示成y(n)=T[ax1(n)+bx2(n)]。当y(n)与y1(n)及y2(n)满足等式y(n)=ay1(n)+by2(n)时,该系统称为线性系统。说的通俗点,看见线性两个字,咋就应该往齐次性和可加性这两方面去想。
二、时不变系统
当输入信号为x(n)时,输出信号用y(n)表示。如果输入为x(n-n0),输出为y(n-n0),即y(n-n0)=T[x(n-n0)],这时,称该系统为时不变系统,此外,我认为由于离散序列多与位的运算有关,我们通常还称其为移不变系统。这里总得来说,信号波形与起点无关。
三、因果系统
如果系统n时刻的输出只与n时刻及以前的输入有关,而与n时刻之后的输入无关,这样的系统称为因果系统。在线性时不变系统中,当n<0时,单位脉冲响应h(n)=0,该系统是因果系统。同样,当一个序列在n<0时,它的数值均为0,则该序列称为因果序列。
常系数差分方程
接下来看看常系数差分方程,实际与常系数微分方程解法差不多,就是用的数据不一样,毕竟一个是连续的,还有一个是离散的。微分方程我们通常要用拉氏变换的方法来求,而这里就要用Z变换方法来求,因为拉氏变换离散之后它就是Z变换。这里之后再讲现在就不多说了。
线性常系数差分方程的求解方法可归纳为下面三种:
(1)经典解法。这类方法类似模拟系统中求微分方程的解法,过程较复杂,简单的说说,其实就是求齐次解和特解,将特解带入差分方程求得它的待定系数,然后将齐次解和特解相加,带入到差分方程当中去,结合边界条件,求得齐次解的系数,而这一结合就是完全解了。
(2)递推法。此方法简单,适用于计算机求解,这个方法说的高大上,要用递归算法,其实就跟我们高中学的等比数列差不多。
(3)变换域法。将时域转换到z域中求解,方法简单易行,当起始状态为零的情况,所得到就是零状态解;当输入为零的时候,就是零输入响应了。之后将详细说明。
AD转换与DA转换
要通过数字方法处理模拟信号,有必要先将它们转换成数字形式,即转换成具有有限精度的数字序列,这一过程称为模数(A/D)转换,而相应的设备称为A/D转换器(ADC)。下图为AD转换器的基本框架。
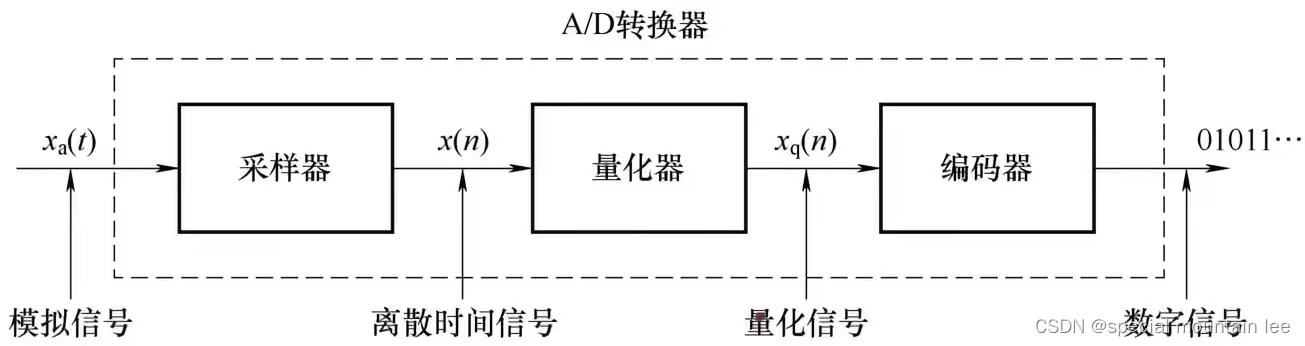
大概以下几个步骤:
(1)采样:采样是连续时间信号到离散时间信号的转换过程,通过对连续时间信号在离散时间点处取样本值获得。因此,如果xₐ(n)是采样器的输入,那么输出是xₐ(nT)=x(n),其中T称为采样间隔,这个是采样最基本的操作,每隔T个位置取个数,当然还有非均匀采样,这里不说了,以后再说。
(2)量化:量化是离散时间连续值信号转换到离散时间离散值(数字)信号的过程。每个信号样本值是从可能值的有限集中选取的。未量化样本x(n)和量化输出xₚ(n)之间的差称为量化误差。
(3)编码:在编码过程中,每一个离散值xₚ(n)由b位的二进制序列表示。
在实际应用的很多场合(例如,语音处理),需要将处理的数字信号转化成模拟信号。将数字信号转化成模拟信号的过程是熟知的数模(D/A)转换。所有D/A转换器通过执行某种插值操作将数字信号的各离散点连接起来,其精度依赖于D/A转换过程的质量。
对模拟信号采样有很多方式。在实际中最常使用的采样类型,即周期采样或均匀采样。可以由下列关系式描述:x(n)=xₐ(nT),式中,x(n)是通过对模拟信号xₐ(t)每隔T(s)取样本值获得的离散时间信号。这一过程,在两个连续的样本之间的时间间隔T称为采样周期或采样间隔,其倒数1/T=Fs称为采样率(样本数/s)或采样频率(Hz)。奈奎斯特采样定理常说,为了能够从采样后的离散信号中完全恢复原始的连续信号,采样频率必须大于等于原始信号最高频率的两倍。因此,这里还需要知道两个概念——过采样和欠采样。过采样指的是对少数类样本进行多次重复采样,使得少数类样本的数量增加,从而使得各类别样本数量相对平衡。过采样可以通过随机复制少数类样本,或者使用更复杂的算法生成新的少数类样本来实现。欠采样则是从多数类样本中随机选择一部分样本,使得多数类样本数量减少,从而达到各类别样本数量相对平衡的目的。但欠采样可能会丢失一些多数类样本中的信息。因此,在工程当中多采用的是过采样。
欲知后事如何,且听下回分解。OVO.......