C++日常刷题积累
- 今日刷题汇总 - day003
- 1、简写单词
- 1.1、题目
- 1.2、思路
- 1.3、程序实现 - 思路1
- 1.4、程序实现 - 思路2(优化)
- 2、dd爱框框
- 2.1、题目
- 2.2、思路
- 2.3、程序实现 - 蛮力法
- 2.4、程序实现 - 同向双指针(滑动窗口)
- 3、除2!
- 3.1、题目
- 3.2、思路
- 3.3、程序实现
- 4、题目链接
今日刷题汇总 - day003
1、简写单词
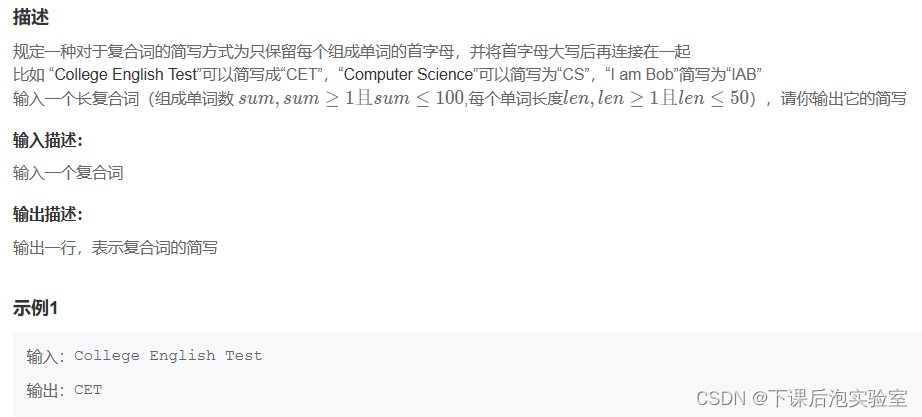
1.1、题目
1.2、思路
首先,读完题,明白就是要求把一段由几个单词组成的字符串,其首字母大写并输出即可。那么,我们很快想到,遍历一遍字符串把单词首字母大写后输出即可。那么,如何确定单词首字母呢?通过观察示例不难看出,每一个空格后接着就是单词的首字母。那么,第一个思路就是先直接判断第一个子母是否为小写字母,是则转换为大写子母后输出,否则直接输出,然后遍历字符串判断是否为空格,是则判断空格的下一个子母是否为小写字母,是则转换为大写后输出,否则直接输出,直到遍历结束即可。
当我做完提交后,发现代码比较冗余,可以进行优化。既然,要输入多个单词,可直接输入一个处理一个单词,直接优化了第一个方法的很多细节的处理。接下来,两个思路都用程序实现一下吧。
1.3、程序实现 - 思路1
首先,按照分析的题目要求写好输入,求得字符串长度,判断只有一个子母时,是否为小写,如果是小写则转换为大写再输出,否则直接输出即可。这里用到了getline函数和size函数以及islower函数和toupper函数。值得注意的是,toupper等函数的返回值,所以需要强转一下。
#include <iostream>
#include <string>
using namespace std;
int main()
{
string word;
getline(cin, word);
size_t n = word.size();
if (n == 1)
{
if (islower(word[0]))
{
cout << (char)toupper(word[0]);
}
else
cout << word[0];
}
else
{
}
return 0;
}
接着,处理字符串长度大于1的情况,如果是只有一个单词,直接像刚才处理的一样判断之后处理输出即可,否则遍历字符串,判断空格,判断空格后的子母,是否处理再输出即可。
#include <iostream>
#include <string>
using namespace std;
int main()
{
string word;
getline(cin, word);
size_t n = word.size();
if (n == 1)
{
if (islower(word[0]))
{
cout << (char)toupper(word[0]);
}
else
cout << word[0];
}
else
{
if (islower(word[0]))
{
cout << (char)toupper(word[0]);
}
else
cout << word[0];
for (int i = 0; i < n; i++)
{
if (word[i] == ' ' && word[i+1])
{
if (islower(word[i + 1])) cout << (char)toupper(word[i + 1]);
else cout << word[i + 1];
}
}
}
return 0;
}
1.4、程序实现 - 思路2(优化)
在思路1基础上进行优化,既然要逐个输入单词,那么直接逐个单词进行判断处理,方便快捷,这种思想称为预处理方法,常用于明确只需要遍历一遍的输入场景。与day002的数组中两个字符串的最小距离,场景逐个输入类似,所以这类场景常用。另外,这样的输入,自动处理了空格,不需要额外对空格的处理。
#include <iostream>
#include <string>
using namespace std;
int main()
{
string word;
while(cin >> word)
{
if(islower(word[0]))
cout << (char)toupper(word[0]);
else
cout << word[0];
}
return 0;
}
额外说明一下,C++的头文件属于是集成了字符串相关的头文件,比如strcmp的头文件,islower的头文件,所以如果是C语言就需要添加<ctype.h>头文件即可。当然不使用,函数也可以利用字符判断。
#include <iostream>
#include <string>
using namespace std;
int main()
{
string word;
while(cin >> word)
{
if('a' <= word[0] && word[0] <= 'z')
cout << (char)(word[0] - 'a' + 'A');
else
cout << word[0];
}
return 0;
}
2、dd爱框框
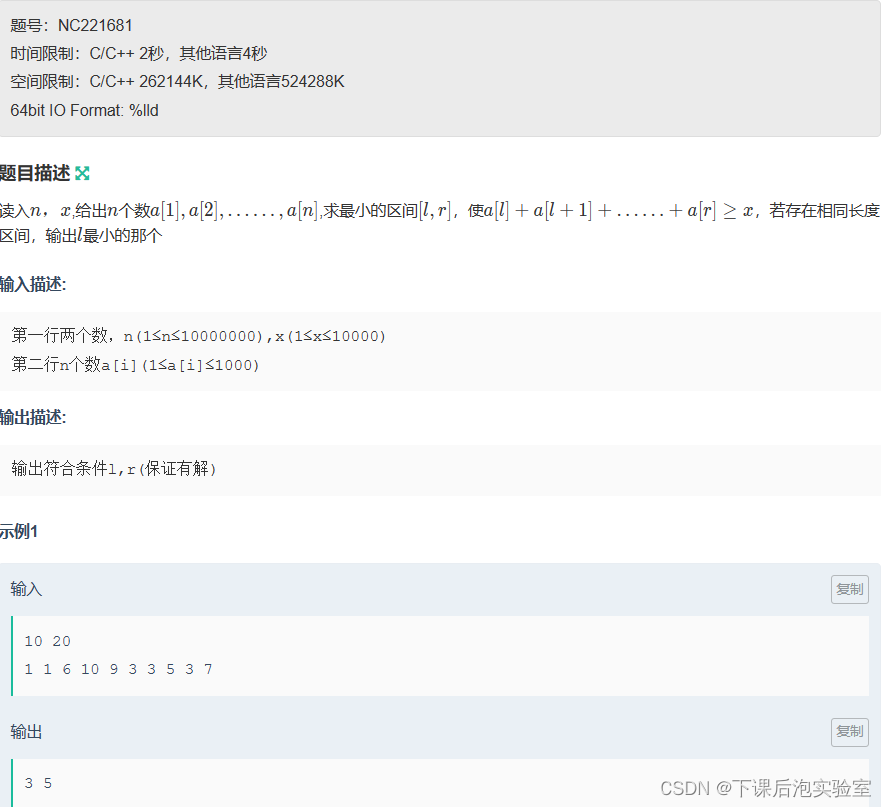
2.1、题目
2.2、思路
首先,读完题,得知,要求一段数组中和最小的区间。既然如此,那么定义一个左区间标志retl和右区间标志retr,那么它们之间的距离retlen最小就是最小区间。那么不难想到蛮力法,利用两层for循环蛮力法,遍历求解,左区间不动,右区间从左区间处,遍历求和,直到sum>=x值时,标记并求得retlen,再将sum置0,左区间++,右区间回到左区间处,继续遍历直到sum>=x值时,再次标记左右区间的位置给retl和retr,然后,依次类推。求得最小区间。其中,注意处理一些细节,此题数组下标是从1开始,如果从0开始输出时需+1,当出现相同长度的retlen时,要处理选择retl最小的哪个区间,此外,得注意题目的数据范围n(1≤n≤10000000),x(1≤x≤10000)和时间2秒以及空间要求,所以使用蛮力法是会出现超时等问题的,不过蛮力法对于个人而言是值得,锻炼编程思维处理一些细节问题的,所以依然写一写蛮力法。
那么此类题,不使用蛮力法,该使用什么方法呢?
再读题,发现,题目的已知条件中权值正整数,即全是>=1的数据,求区间就涉及到两个指针的操作变换关系且两个指针遍历方向一致,所以更好的方法是采用同向双指针法,即典型的滑动窗口法。这也是这道题的主要考点而不是蛮力法。
那么滑动窗口方法的步骤,通常需要四步:
(1)、进窗口:对于此题就是,sum += a[right];
(2)、判断条件:对于此题就是,sum >= x;
(3)、指针关系的更新,即结果更新:对于此题就是,right-left+1 < retlen;
(4)、出窗口:对于此题就是,sum -= a[left];
接下来就是程序实现。
2.3、程序实现 - 蛮力法
首先,按照思路的分析,定义好变量和数据范围,写好输入和两层for循环,
#include <iostream>
#include <climits>
using namespace std;
const int N = 1e7 + 10;
int main()
{
int n, x;
cin >> n >> x;
int a[N];
for (int i = 1; i < n; i++)
{
cin >> a[i];
}
int sum = 0;
int retl,retr;
int retlen = INT_MAX;
for (int i = 1; i < n; i++)
{
for (int j = i; j < n; j++)
{
sum += a[j];
if (sum >= x)
{
}
}
sum = 0;
}
cout << retl << ' ' << retr;
return 0;
}
接着处理,一些细节问题,当出现相同长度的retlen时,直接break,且处理retlen更新时才置换retr和retl的值。
#include <iostream>
#include <climits>
using namespace std;
const int N = 1e7 + 10;
int main()
{
int n, x;
cin >> n >> x;
int a[N];
for (int i = 1; i < n; i++)
{
cin >> a[i];
}
int sum = 0;
int retl,retr;
int retlen = INT_MAX;
for (int i = 1; i < n; i++)
{
for (int j = i; j < n; j++)
{
sum += a[j];
if (sum >= x)
{
if (j - i == retlen)
{
sum = 0;
break;
}
if (retlen > j - i)
{
retlen = min(retlen, j - i);
retl = i;
retr = j;
}
sum = 0;
break;
}
}
sum = 0;
}
cout << retl << ' ' << retr;
return 0;
}
注意题目的数据范围n(1≤n≤10000000),x(1≤x≤10000)和时间2秒以及空间要求,所以使用蛮力法是会出现超时等问题的。由于是蛮力法,所以超时也毋庸置疑。
2.4、程序实现 - 同向双指针(滑动窗口)
接下来,在蛮力法基础上进行优化,为了方便描述左区间定义为left,右区间为right,再定义retLen 、retLeft 、retRight,分别存放步骤3的更新结果和更新的左区间以及更新的右区间。然后根据步骤(1)、进窗口:对于此题就是,sum += a[right];
(2)、判断条件:对于此题就是,sum >= x;
(3)、指针关系的更新,即结果更新:对于此题就是,right-left+1 < retlen;
(4)、出窗口:对于此题就是,sum -= a[left];
编写程序即可。
#include <iostream>
#include <climits>
using namespace std;
const int N = 1e7 + 10;
int main()
{
int n, x;
cin >> n >> x;
int a[N];
for (int i = 1; i < n; i++)
{
cin >> a[i];
}
int left = 0, right = 0, sum = 0;
int retLen = N, retLeft = -1, retRight = -1;
while(right <= n)
{
sum += a[right];//步骤一
while(sum >= x)//步骤二
{
if(right - left + 1 < retLen)//步骤三
{
retLeft = left;
retRight = right;
retLen = right - left + 1;
}
sum -= a[left++];//步骤四,这里不好理解可以理解为上面蛮力法中的将右区间置回左区间处,方便重新求sum的意思。所以这里就是左区间窗口向右缩,类似于KMP算法不用让右区间回置,从而实现的优化。
}
right++;
}
cout << retLeft << " " << retRight << endl;
return 0;
}

3、除2!
3.1、题目
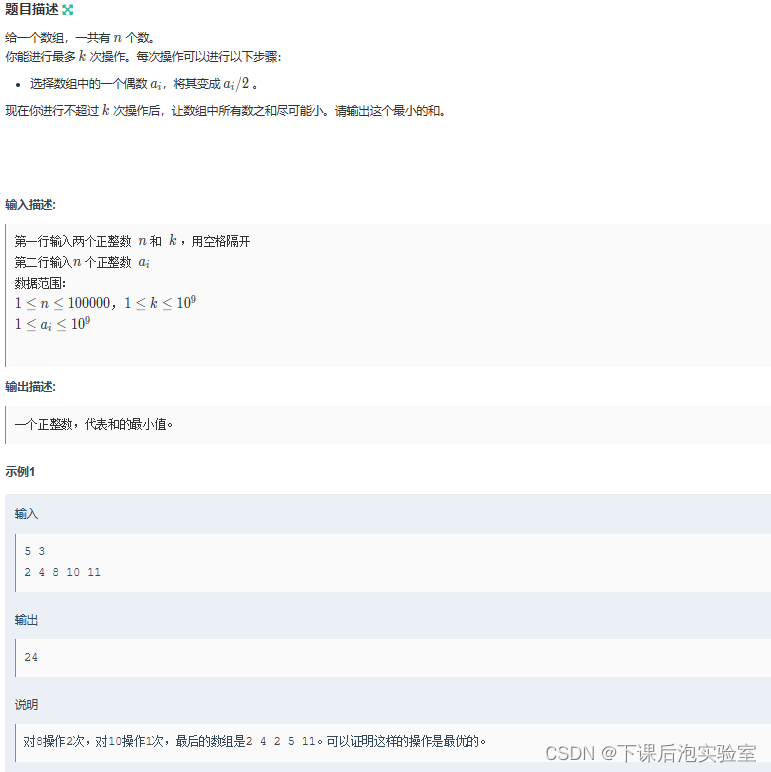
3.2、思路
首先,读完题,明白要求实现一组n个数据的和sum最小,且可对偶数进行k次除2操作。分析示例,就能看出,只需要每一次操作都对当前这组数据的最大的偶数进行除2即可,这样求得的和就是最小的。那么,很快想到熟悉的数据结构堆的特性,利用其中的大根堆就可以巧妙的完成每次对最大的偶数操作,所以堆中数据就只需要存放偶数即可。另外,值得注意的是,在堆顶最大偶数进行除2操作后,得让它pop出堆,使第二大的偶数存放至堆顶,便于下一次操作,而且还需要判断堆顶除2操作完成后,是否仍然是偶数,那么继续进堆排队即可。此外,我在写这道题时,总是超时发现,数据范围是10^9,所以这里需要用long long,接下来就是程序实现。
3.3、程序实现
首先,按照题目数据范围要求定义变量,写好输入,并且依然可以采用预处理方式不用建立数组,减少空间消耗,然后巧妙地利用priority_queue特性(底层就是大根堆)定义大根堆heap,再输入n个数据,求输入数的和,并把偶数建堆。
#include <iostream>
#include <queue>
using namespace std;
int main()
{
long long n,k;
cin >> n >> k;
long long a,sum = 0;
//巧妙利用大根堆
priority_queue<long long> heap;
while(n--)
{
cin >> a;
sum += a;
if(a % 2 == 0)
heap.push(a);
}
return 0;
}
接着,开始进行除2操作k次,当然得保证堆中还有偶数,即heap.size()为真才进行操作,然后定义一个中间变量temp,存放堆顶除2操作后的数据,再pop堆顶让第二大的偶数,放置堆顶,然后sum减去变量temp,就是当前一次操作后的最小和,如果堆顶除2操作后还是偶数继续进堆,依此类推,直到k次操作完成或堆中没有偶数结束即可。
#include <iostream>
#include <queue>
using namespace std;
int main()
{
long long n,k;
cin >> n >> k;
long long a,sum = 0;
//巧妙利用大根堆
priority_queue<long long> heap;
while(n--)
{
cin >> a;
sum += a;
if(a % 2 == 0)
heap.push(a);
}
while(heap.size() && k--)
{
long long temp = heap.top() / 2;
heap.pop();
sum -= temp;
if(temp % 2 == 0)
heap.push(temp);
}
cout << sum << endl;
return 0;
}
4、题目链接
简写单词
dd爱框框
除2!