---

今日所学：

今天我学习了神经网络训练的核心原理，主要是反向传播算法。这个过程包括将模型预测值（logits）和正确标签（label）输入到损失函数（loss function）中计算loss，然后通过反向传播算法计算梯度（gradients），最终更新模型参数（parameters）。自动微分技术能够在某点计算可导函数的导数值，是反向传播算法的一个广义实现。它的主要作用是将复杂的数学运算分解为一系列简单的基本运算，从而屏蔽了大量求导的细节和过程，显著降低了使用深度学习框架的门槛。

MindSpore采用函数式自动微分的设计理念，提供了更接近数学语义的自动微分接口，例如grad和value_and_grad。为了更好地理解这些概念，我还学习了如何使用一个简单的单层线性变换模型进行实践。

---

一、函数与计算图

MindSpore之前的还不熟悉的相关内容可以见：《昇思25天学习打卡营第1天|基本介绍》

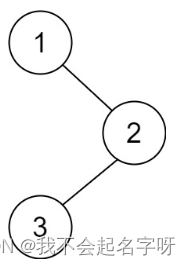
计算图是一种借助图论来描绘数学函数的一种方法，同时也是深度学习框架用以表达神经网络模型的通用方式。以下，我们将以此计算图为基础，来构建计算函数和神经网络：

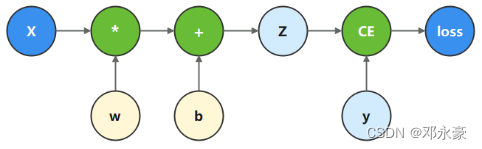
在本节所学的这个模型中，𝑥为输入，𝑦为正确值，𝑤和𝑏是我们需要优化的参数，根据计算图描述的计算过程，构造计算函数，执行计算函数，可以获得计算的loss值，代码与结果如下所示：

x = ops.ones(5, mindspore.float32)  # input tensor
y = ops.zeros(3, mindspore.float32)  # expected output
w = Parameter(Tensor(np.random.randn(5, 3), mindspore.float32), name='w') # weight
b = Parameter(Tensor(np.random.randn(3,), mindspore.float32), name='b') # bias

def function(x, y, w, b):
    z = ops.matmul(x, w) + b
    loss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))
    return loss

loss = function(x, y, w, b)
print(loss)

结果如下：

Tensor(shape=[], dtype=Float32, value= 0.914285)

二、微分函数与梯度计算

在之后学习内容中为了优化模型参数，需要求参数对loss的导数：

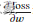
和

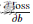
此时我们调用mindspore.grad函数，来获得function的微分函数。其中grad函数的两个入参，分别为fn（待求导的函数）与grad_position（指定求导输入位置的索引），代码如下：

grad_fn = mindspore.grad(function, (2, 3))
grads = grad_fn(x, y, w, b)
print(grads)

结果如下：

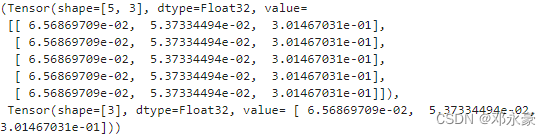
使用grad获得微分函数是一种函数变换，即输入为函数，输出也为函数。

三、Stop Gradient

在常规的情况下，求导操作主要是计算loss相对于参数的导数，由此，函数的输出仅有loss一项。然而，当我们期望函数有多项输出时，微分函数将会计算所有输出项相对于参数的导数。在这种情况下，如果我们希望实现特定输出项的梯度截断，或者需要消除某个Tensor对梯度的影响，那么我们将需要使用Stop Gradient操作。在这里，我们会将function改造成同时输出loss和z的function_with_logits，并获取微分函数以供执行。

如果想要屏蔽掉z对梯度的影响，即仍只求参数对loss的导数，可以使用ops.stop_gradient接口，将梯度在此处截断。

代码如下：

def function_with_logits(x, y, w, b):
    z = ops.matmul(x, w) + b
    loss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))
    return loss, z

grad_fn = mindspore.grad(function_with_logits, (2, 3))
grads = grad_fn(x, y, w, b)
print(grads)

def function_stop_gradient(x, y, w, b):
    z = ops.matmul(x, w) + b
    loss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))
    return loss, ops.stop_gradient(z)

grad_fn = mindspore.grad(function_stop_gradient, (2, 3))
grads = grad_fn(x, y, w, b)
print(grads)

截断前结果：

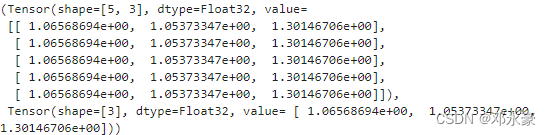
截断后结果：

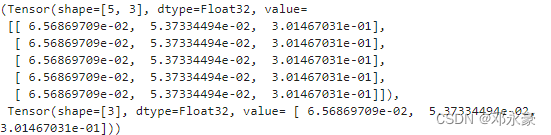
四、Auxiliary data

我深入理解了Auxiliary data（辅助数据）的概念和应用。我明白了辅助数据其实就是函数的非主要输出项。在实际应用中，我们常将函数的主要输出设为loss，而其它的所有输出则被视为辅助数据。对于grad和value_and_grad函数，我享受到了has_aux参数带来的便利。当将其设为True，它就能自动实现之前需要手动添加的stop_gradient操作。这种设计巧妙地使我在返回辅助数据的同时，不受梯度计算的任何影响。

在后续的实践中，我继续使用了function_with_logits，并设置了has_aux为True进行操作。整个过程顺畅无比，加深了我对这一主题的理解。我会持续探索，并将这些知识应用到更广泛的场景中去：

grad_fn = mindspore.grad(function_with_logits, (2, 3), has_aux=True)

grads, (z,) = grad_fn(x, y, w, b)
print(grads, z)

结果如下：

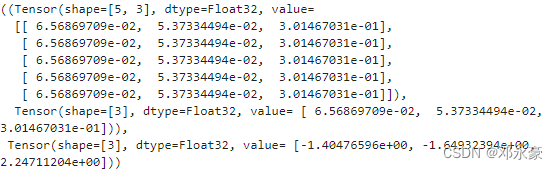
五、神经网络梯度计算

前面章节已经讲述了网络构建，还不了解的可见这篇文章：《昇思25天学习打卡营第6天|网络构建》

接下来，我深入了解了如何通过Cell去构造神经网络，以及利用函数式自动微分来实现反向传播的过程。我首先继承了nn.Cell来构建单层线性变换神经网络。有意思的是，这个过程中我直接使用了之前的 𝑤 和 𝑏 来作为模型参数。这种做法完全打破了我早前的理解，让我认识到原来我们可以直接使用现有的参数以节约时间和计算资源。我将这些参数用mindspore.Parameter包装起来作为内部属性，并在construct内实现了与之前一样的Tensor操作：

# Define model
class Network(nn.Cell):
    def __init__(self):
        super().__init__()
        self.w = w
        self.b = b

    def construct(self, x):
        z = ops.matmul(x, self.w) + self.b
        return z
        
# Instantiate model
model = Network()
# Instantiate loss function
loss_fn = nn.BCEWithLogitsLoss()

# Define forward function
def forward_fn(x, y):
    z = model(x)
    loss = loss_fn(z, y)
    return loss
    
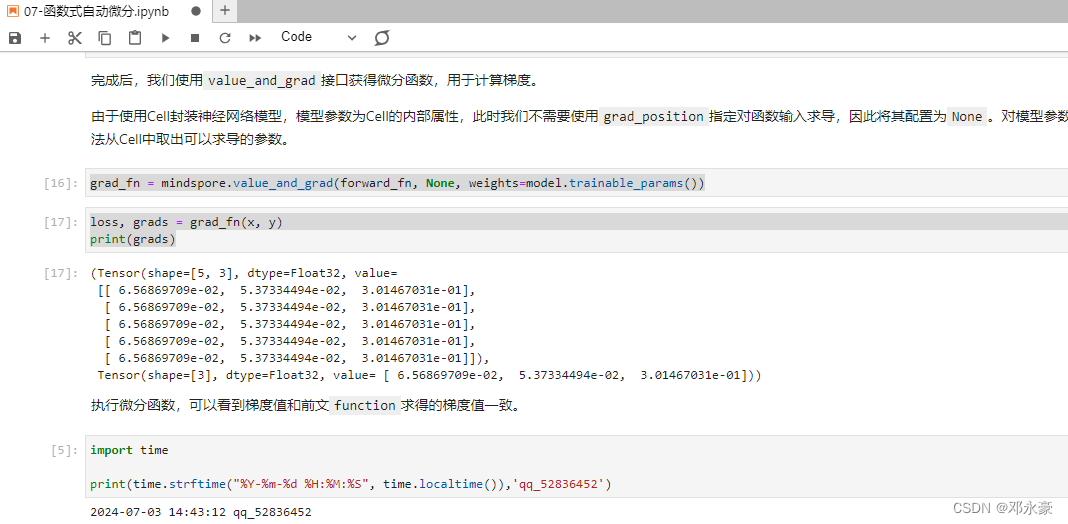
grad_fn = mindspore.value_and_grad(forward_fn, None, weights=model.trainable_params())

loss, grads = grad_fn(x, y)
print(grads)

结果如下：

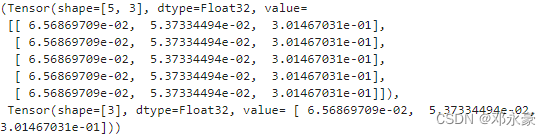
可以看出，执行微分函数后的梯度值和前文function求得的梯度值一致。

总结

在今天的学习中，我深入理解了神经网络训练的核心原理，包括反向传播算法和如何利用自动微分技术来计算梯度并更新模型参数。我也学习了如何使用MindSpore框架的函数式自动微分接口来进行实践，并利用计算图进行模型参数优化。此外，我理解了Stop Gradient操作和辅助数据对梯度计算的影响，以及如何在神经网络的梯度计算中有效利用它们。通过理论学习和实践操作，我对这些概念有了更深入的理解，期待在明天的学习中继续进步。