定义

线性模型非常常见，但详细了解其中原理是必要的。

一般将样本特征进行线性组合达到预测的目标，如表达式$y=f(X;W)+b$,其中$X$为输入的样本数据，$W$为权重系数，$b$为偏置系数。

如对于图片样本，一种处理方式为将图片像素矩阵转化为维度向量，如$X=[x_1,x_2,...,x_n],W=[w_1,w_2,...,w_m],b=[b_1,b_2,...,b_n]$，输出$y$，$y$可以表示为类别0或者1，而0或者1代表不同类别，从而实现预测。

在实际运用中，如分类问题，y只有两个离散值0或者1，那么如果使用函数值直接输出（此函数值域为实数），无法达到0或者1的唯二输出目的。存在的一种解决方案有：通过使用决策函数（非线性函数）输出预测结果，如用$g(y)$表示，也即$g(f(X;W)+b)$,该决策函数在二分类中可为$sgn$函数（下图从百度知道获取）

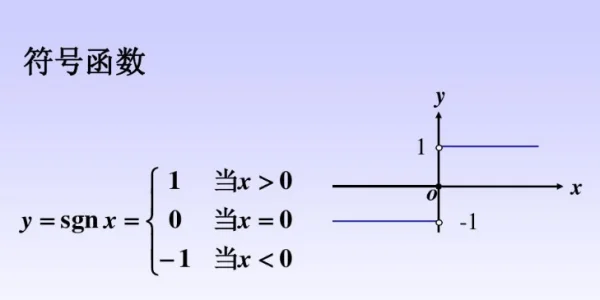
当然，对于此处的二分类，我们忽略$x=0$的取值，不进行预测。

---

二分类与多分类

从数学层面上来讲，对于二分类的问题，如果将输入的样本视为高维空间中的点，如三位空间，那么进行二分类就是寻找一个超平面（或称为决策平面），将这些样本点从空间上分为两个部分，每个部分对应一个类别。

每一个样本点到决策平面的距离可根据点到直线的（有向）距离公式求得，即$dist=\frac{f(X;W)+b}{||W||}$（为了便于描述，若二分类问题，样本的特征向量为二维向量，那么只需要对于二维组成的平面找一条决策线即可将二维平面分为两部分，所以此处使用的是点到直线的距离公式）

进一步定义
$$\begin{array}{rl}f(X;W)+b& >0ify=1\\ f(X;W)+b& <0ify=-1\end{array}$$
找到该决策直线的关键点在于找到线性模型中的参数$w$的最优解，满足$y(f(X;W)+b)>0$
采取的损失函数在后续内容涉及

在实际应用中，二分类常常不满足需要，多分类需要被纳入讨论。

• 最直接的办法是将多分类的问题分解为多个二分类的问题，如分为猫、狗、猪三类，我们可以分为猫和其他类、狗和其他类、猪和其他类，但是该方法较为繁琐且时间复杂度高。
• 在第一种方法进行改进，分类的目的在于把每一个不同的类型识别出来，那么由完全图的关系可知，若有n个类别，那么我们需要进行n(n-1)/2次二分类操作，较于方法一，在比较次数上有所减少。
• 最后，如果能够实现只需一个过程可以同时判别n个类别，那么将会是最好的解决方案。

当然，数学家们提出一种解决方法（基于前面方法优化）：$f(x;w)+b$函数存在一个性质，满足对于某个样本，若属于类别$c_1$,不属于类别$c_1$使用$\widehat{c_1}$表示,那么$f_{c_1}(x;w_{c_1})+b>f_{\widehat{c_1}}(x;w_{\widehat{c_1}})+b$。这个表示意思就是样本属于哪一个类别，则该类别的预测值最大，非该类别的预测值较小。
$$\begin{array}{r}y=argmax{f}_c(x;w_c),c\in [1,C]\end{array}$$
那么该函数对于不同类别的输出值不同的关键在于权重参数$w$不同，如果存在n个类别，那么权重参数$w$的维度应该为n，即$[w_1,w_2,...,w_n]$

第三种方法与第一种方法相比，具有很大的类似之处，都需要n类别n个判别器，但是第三种方法较于第一种方法的好处在于第一种方法存在难以确定类别的情况，如对于某个样本，多个分类都说属于自己的类别，都满足类别阈值，造成难以区分境况，而第三种恰好弥补了该缺点，第三种为所有输出中取值最高。

---

Logistic回归

Logistic回归常用于处理线性模型中的二分类问题。

逻辑回归的关键点在于引入非线性函数$g(f)$，将预测值限制在(0,1)之间,也可称为概率。

如对于二分类问题，样本x，$p(y=1|x)$为x属于类别1的后验概率，也可表示为$g(f(x;w))$。

逻辑函数表示为
$$\begin{array}{rl}p(y=1|\mathbf{x})& =\frac{1}{1+e^{-w^{T}x}}\\ p(y=0|\mathbf{x})& =1-\frac{1}{1+e^{-w^{T}x}}\\ & =\frac{e^{-w^{T}x}}{1+e^{-w^{T}x}}\end{array}$$
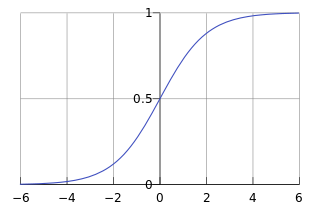
该函数也就是常见的$sigmoid$函数

对于二分类模型关键在于参数$w$，那么对如对$p(y=1|\mathbf{x})=\frac{1}{1+e^{-w^{T}x}}$变换可得
$$\begin{array}{rl}{w}^{T}x& =log\frac{p(y=1|x)}{1-p(y=1|x)}\\ & =log\frac{p(y=1|x)}{p(y=0|x)}\end{array}$$

那么预测值即为$log\frac{p(y=1|x)}{p(y=0|x)}$或者$log\frac{p(y=0|x)}{p(y=1|x)}$，根据值的大小判定类别。

总之，逻辑回归分类通过属于某个类别的概率值来判断是否属于某个类别，并且这个类别默认标记为1(如大于0.5)，另外的一个类别会标记为0(小于0.5)。

那么如何更新权重系数$w$我们关心的问题，常用的一种方法即使用交叉熵损失函数与梯度下降法进行参数更新。

对于样本数据$x,y$,预测输出值$\hat{y}=\sigma (w^{T}x)$。在二分类中，样本真实标签为两类值(0 and 1),输出为如下所示
$$\begin{array}{rl}p(y=1|\mathbf{x})& =y\\ p(y=0|\mathbf{x})& =1-y\end{array}$$
实际情况下存在损失，损失函数可表示为
$$\begin{array}{rl}Loss& =-\frac{1}{N}\sum _{n=1}^N(p(y=1|\mathbf{x})log\hat{y}+p(y=0|\mathbf{x})log(1-\hat{y}))\\ & =-\frac{1}{N}\sum _{n=1}^N(ylog\hat{y}+(1-y)log(1-\hat{y}))\end{array}$$

对参数$w$求导可得,$w=-\frac{1}{N}{\sum }_{n=1}^N(x(y-\hat{y}))$
更新参数,$w=w+\alpha \frac{1}{N}{\sum }_{n=1}^N(x(y-\hat{y}))$

---

Softmax回归

softmax回归是对于logistic回归的扩展，从二分类延伸到多分类问题。

二分类中使用0或者1代表两个类别，而多分类（若有n个类别）中使用n个数字代表类别，那么后验概率可表示为
$$\begin{array}{rl}p(y=c|\mathbf{x})& =\frac{e^{-w_c^{T}x}}{{\sum }_{c=1}^C{e}^{-w_c^{T}x}}\end{array}$$

同理，交叉熵损失函数为(此处芦苇不同于二分类原因在于多分类损失函数将每一个类损失都相加，二分类中同时将两个类别的损失相加)
$$\begin{array}{r}Loss=-\frac{1}{N}\sum _{n=1}^N\sum _{c=1}^C{y}_{c}log{\hat{y}}_c\end{array}$$
其他处理一致。