一、并查集模板
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
并查集高效率的核心是一旦更新过一次后,就会将路径压缩掉,避免后续重复遍历路径。
二、并查集应用
1、格子游戏

分析:每构成一个方框,当最后两个点连接时,两个点的祖宗必定是同一个,所以此题就转化为并查集问题,但本题需要把二维坐标转化为一维。
如何把二维坐标转化为一维?
0 1 2 //3X3坐标系转化为一维各个点对应的数值如左图所示
3 4 5 //二维转一维必须从0 0点开始
6 7 8 //如果从1 1点开始,只需x-- y--
//二维坐标(x,y) 对应的数值————> z = x*n+y , n为坐标系的大小 代码
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 40010;
int p[N];
int n,m;
int get(int x,int y)
{
return x*n+y;
}
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int main()
{
cin>>n>>m;
for(int i=0;i<n*n;i++) p[i]=i;
int res=0;
for(int i=1;i<=m;i++)
{
int x,y;
char d;
cin>>x>>y>>d;
x--,y--;
int a=get(x,y);
int b;
if(d=='D') b=get(x+1,y);
else b=get(x,y+1);
int pa=find(a),pb=find(b);
if(pa==pb)
{
res=i;
break;
}
p[pa]=pb;
}
if(!res) puts("draw");
else cout<<res<<endl;
return 0;
}2、搭配购买(并查集+01背包)

分析:云朵绑定购买,相当于把所有绑定的云朵堪为一朵,然后可以买的最大价值,问题转化为利用并查集把绑定的云朵看为一朵,然后01背包求最大价值。
怎样把所有绑定的云朵和价值合并到一块?
利用并查集的思想所有祖宗节点的体积和价值,就可以看为整个连通块的体积和价值。
代码
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 10010;
int v[N],w[N];
int f[N];
int p[N];
int n,m,vol;
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int main()
{
cin>>n>>m>>vol;
for(int i=1;i<=n;i++) p[i]=i;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
//并查集
for(int i=1;i<=m;i++)
{
int a,b;
cin>>a>>b;
int pa=find(a),pb=find(b);
if(pa!=pb)//祖宗节点对应整个连通块的体积和价值
{
v[pb]+=v[pa];
w[pb]+=w[pa];
p[pa]=pb;
}
}
//01背包
for(int i=1;i<=n;i++)
{
if(p[i]==i)
{
for(int j=vol;j>=v[i];j--)
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[vol]<<endl;
return 0;
}3、程序自动分析(离散话+并查集)

分析:由于 i,j的数据范围较大,所以本题得把数据离散化(映射为1~n的值);
离散化
1.保序离散化(排序+判重+二分)
2.不保序离散化(hash表映射)本题为不保序离散化,注意初始化1~n的祖宗,n为映射的不同节点的个数
代码
#include<iostream>
#include<algorithm>
#include<unordered_map>
using namespace std;
const int N = 200010;
int p[N];
unordered_map<int,int> S;
int n,m;
struct QUERY{
int x,y,e;
}query[N];
int get(int x)//不保序离散化
{
if(S.count(x)==0) S[x]=++n;//判断该数是否存在,n从0开始
return S[x];
}
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
n=0; //从0开始
scanf("%d",&m);
S.clear();//注意清空
for(int i=0;i<m;i++)
{
int x,y,e;
scanf("%d%d%d",&x,&y,&e);
query[i]={get(x),get(y),e};
}
for(int i=1;i<=n;i++) p[i]=i;
for(int i=0;i<m;i++)
{
if(query[i].e==1)
{
int pa=find(query[i].x),pb=find(query[i].y);
p[pa]=pb;
}
}
int flag=0;
for(int i=0;i<m;i++)
{
if(query[i].e==0)
{
int pa=find(query[i].x),pb=find(query[i].y);
if(pa==pb)
{
flag=1;
break;
}
}
}
if(flag) puts("NO");
else puts("YES");
}
return 0;
}4、银河英雄传说

分析:本题为路径维护题,维护子节点到根节点的距离。注意更新祖宗时所更新的所有内容
解题思路:把 i 舰队放到 j 舰队后面的操作:首先找到i与j的祖宗,如果两个祖宗不一样,那么更新
s数组(表示该连通块的大小)d数组(表示每个子节点到祖宗的长度),p数组。
当更新一次d数组后,d[x] = d[x](表示该节点到没更新祖宗前的距离)+d[p[x]](表示该节点到没更新祖宗前的祖宗,到的更新后祖宗的距离)如下图所示
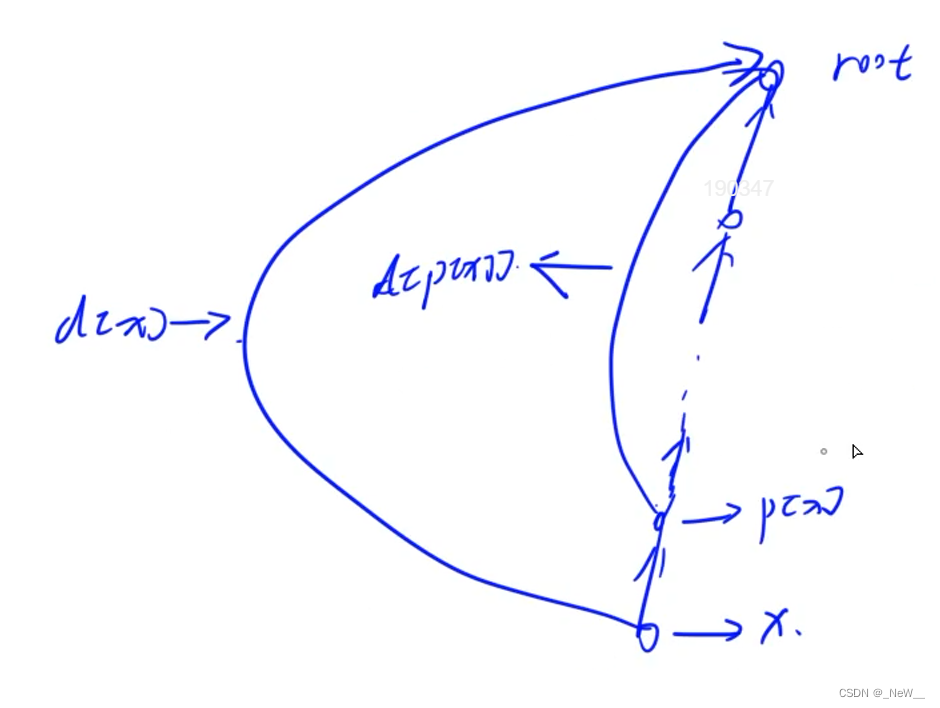
两个节点之间的距离:abs(d[a]-d[b])-1;当两个节点相同时结果为0,需要用max特判
代码
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 30010;
int p[N],d[N],s[N];
int n,m;
int find(int x)
{
if(p[x]!=x)
{
int root=find(p[x]);
d[x]+=d[p[x]];
p[x]=root;
}
return p[x];
}
int main()
{
int T;
scanf("%d",&T);
for(int i=1;i<N;i++ )
{
p[i]=i;
s[i]=1;
}
while(T--)
{
char op[2];
int a,b;
scanf("%s%d%d",op,&a,&b);
if(op[0]=='M')
{
int pa=find(a),pb=find(b);
if(pa!=pb)//注意更新的内容
{
d[pa]=s[pb];
s[pb]+=s[pa];
p[pa]=pb;
}
}
else
{
int pa=find(a),pb=find(b);
if(pa!=pb) puts("-1");
else printf("%d\n",max(0,abs(d[a]-d[b])-1));//两点相同时取0
}
}
return 0;
}5.奇偶游戏

分析:根据前缀和的思想(A只为0或 1 )
假设Si=A1+A2+......+Ai;
那么S[l,r]是奇数就相当于Sr-S(l-1) 中有奇数个1,同理偶数是一样的。
前缀和的思想可以转化为在同一个集合里维护每一个点与祖宗的关系可以推出点与点之间的关系。(d数组的值为1,说明与祖宗关系不同,0说明相同)
如果两个数状态相反,那么说明他们之间有奇数个1.
异或运算相当于不进位加法,并且可以表示在模2的情况下计算
#include<iostream>
#include<algorithm>
#include<string>
#include<unordered_map>
using namespace std;
const int N = 10010;
int n,m;
int p[N];
int d[N];
unordered_map<int,int> S;
int get(int x)
{
if(S.count(x)==0) S[x]=++n;
return S[x];
}
int find(int x)
{
if(p[x]!=x)
{
int root=find(p[x]);
d[x]^=d[p[x]];
p[x]=root;
}
return p[x];
}
int main()
{
scanf("%d%d",&n,&m);
n=0;
for(int i=1;i<N;i++) p[i]=i;
int res=m;
for(int i=1;i<=m;i++)
{
string op;
int a,b;
scanf("%d%d",&a,&b);
cin>>op;
a=get(a-1),b=get(b);
int t=0;
if(op=="odd") t=1;
int pa=find(a),pb=find(b);
if(pa==pb)
{
if((d[a]^d[b])!=t)
{
res=i-1;
break;
}
}
else
{
p[pa]=pb;
d[pa]=d[a]^d[b]^t;
}
}
cout<<endl;
cout<<res<<endl;
return 0;
}(2)合并集合的做法,维护两个集合,同一类的放到一个集合
如果a和b为同一类的话把a的祖先设为b, a+M的祖先设为 b+M
如果a+M和b为同一类的话把a+M的祖先设为b,a的祖先设为b+M
#include<iostream>
#include<algorithm>
#include<string>
#include<unordered_map>
using namespace std;
const int N = 40010,M=N/2;
int n,m;
int p[N];
int d[N];
unordered_map<int,int> S;
int get(int x)
{
if(S.count(x)==0) S[x]=++n;
return S[x];
}
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int main()
{
scanf("%d%d",&n,&m);
n=0;
for(int i=1;i<N;i++) p[i]=i;
int res=m;
for(int i=1;i<=m;i++)
{
string op;
int a,b;
scanf("%d%d",&a,&b);
cin>>op;
a=get(a-1),b=get(b);
int pa=find(a),pb=find(b);
int pa1=find(M+a),pb1=find(M+b);
if(op=="odd")
{
if(pa==pb)
{
res=i-1;
break;
}
p[pa1]=pb;
p[pa]=pb1;
}
else
{
if(pa1==pb)
{
res=i-1;
break;
}
p[pa]=pb;
p[pa1]=pb1;
}
}
cout<<res<<endl;
return 0;
}