目录
Python 库及 MindSpore 相关模块和类的导入
函数与计算图
微分函数与梯度计算
Stop Gradient
Auxiliary data
神经网络梯度计算
Python 库及 MindSpore 相关模块和类的导入
Python 中的 numpy 库被成功导入,并简称为 np。numpy 在科学计算领域应用广泛,其为用户提供了高效便捷的数组操作方式以及丰富的数学函数。此外,mindspore 这一特定的深度学习框架或与之相关的库也被引入。从 mindspore 库中,nn 模块被导入,该模块涵盖了与神经网络相关的各类类和函数。同时,ops 模块也从 mindspore 库中被引入,其中包含了多种多样的操作符或者操作函数。不仅如此,Tensor(张量)和 Parameter(参数)这两个类也从 mindspore 库中被导入,它们主要用于构建以及处理模型当中的数据和参数。
代码如下:
import numpy as np
import mindspore
from mindspore import nn
from mindspore import ops
from mindspore import Tensor, Parameter函数与计算图
计算图乃是借助图论的语言来呈现数学函数的一种形式,同时也是深度学习框架用以表述神经网络模型的统一手段。接下来,我们会依据下面的计算图来构建计算函数以及神经网络。
代码如下:
x = ops.ones(5, mindspore.float32) # input tensor
y = ops.zeros(3, mindspore.float32) # expected output
w = Parameter(Tensor(np.random.randn(5, 3), mindspore.float32), name='w') # weight
b = Parameter(Tensor(np.random.randn(3,), mindspore.float32), name='b') # bias
def function(x, y, w, b):
z = ops.matmul(x, w) + b
loss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))
return loss
loss = function(x, y, w, b)
print(loss) 分析:在 MindSpore 框架中定义了一些张量和参数,并定义了一个计算函数,最后调用该函数并打印结果。
首先,定义了输入张量 x 为全 1 的 5 维张量,期望输出 y 为全 0 的 3 维张量,权重 w 为 5×3 的随机张量,偏置 b 为 3 维的随机张量。
然后,定义了一个名为 function 的函数,在函数内部:
首先通过矩阵乘法 ops.matmul(x, w) 计算 x 和 w 的乘积,再加上偏置 b 得到 z 。
接着使用 ops.binary_cross_entropy_with_logits 函数计算 z 和 y 之间的二元交叉熵损失,其中还使用了两个全 1 的张量作为其他参数。
最后,调用 function 函数并传入之前定义的 x、y、w、b ,将计算得到的损失值赋给 loss 并打印出来。
运行结果:
3.1194968
微分函数与梯度计算
为了实现对模型参数的优化,必须求得参数针对损失(loss)的导数。在此情形下,我们调用 mindspore.grad 函数,从而获取关于 function 的微分函数。
这里所运用的 grad 函数包含两个输入参数,其一为 fn :即有待进行求导操作的函数;其二为 grad_position :用于明确指定求导输入位置的索引。
代码如下:
grad_fn = mindspore.grad(function, (2, 3))
grads = grad_fn(x, y, w, b)
print(grads)
分析:定义了一个名为“grad_fn”的梯度计算函数,此函数旨在计算“function”针对输入值“(2, 3)”的梯度情况。运用此前所定义的梯度计算函数“grad_fn”,针对变量“x”、“y”、“w”以及“b”进行梯度的计算操作,并将所得结果存置于“grads”之中。最后通过“print(grads)”语句,将计算得出的梯度“grads”予以打印输出,从而能够方便查看梯度的具体数值情况。
运行结果:
(Tensor(shape=[5, 3], dtype=Float32, value=
[[ 3.31783742e-01, 3.25132251e-01, 8.20241794e-02],
[ 3.31783742e-01, 3.25132251e-01, 8.20241794e-02],
[ 3.31783742e-01, 3.25132251e-01, 8.20241794e-02],
[ 3.31783742e-01, 3.25132251e-01, 8.20241794e-02],
[ 3.31783742e-01, 3.25132251e-01, 8.20241794e-02]]), Tensor(shape=[3], dtype=Float32, value= [ 3.31783742e-01, 3.25132251e-01, 8.20241794e-02])) Stop Gradient
通常而言,在求导过程中,往往会求取损失(loss)对参数的导数,所以函数的输出一般仅有损失这一项。而当我们期望函数能够输出多项时,微分函数将会对所有的输出项针对参数进行求导。此时,倘若想要达成对某个输出项的梯度截断,或者消除某个张量(Tensor)对梯度的影响,就需要运用停止梯度(Stop Gradient)这一操作。
代码如下:
def function_with_logits(x, y, w, b):
z = ops.matmul(x, w) + b
loss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))
return loss, z
grad_fn = mindspore.grad(function_with_logits, (2, 3))
grads = grad_fn(x, y, w, b)
print(grads)
def function_stop_gradient(x, y, w, b):
z = ops.matmul(x, w) + b
loss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))
return loss, ops.stop_gradient(z)
grad_fn = mindspore.grad(function_stop_gradient, (2, 3))
grads = grad_fn(x, y, w, b)
print(grads) 分析:首先定义了一个名为 function_with_logits 的函数,它接受 x、y、w 和 b 作为参数,通过矩阵乘法和加法计算 z,并基于 z 和 y 计算二分类交叉熵损失 loss 。然后使用 mindspore.grad 计算这个函数关于第 2 和第 3 个参数(可能是 w 和 b )的梯度,并将结果存储在 grad_fn 中。通过调用 grad_fn 并传入相应的参数,获取梯度并打印输出。
接下来又定义了一个名为 function_stop_gradient 的函数,与前面类似,但对 z 使用了 ops.stop_gradient 操作,这通常用于阻止对 z 的梯度计算。同样计算这个函数关于第 2 和第 3 个参数的梯度,并打印输出。
总的来说,这段代码是在探索不同函数设置下梯度计算的结果和差异。
运行结果:
(Tensor(shape=[5, 3], dtype=Float32, value=
[[ 1.33178377e+00, 1.32513225e+00, 1.08202422e+00],
[ 1.33178377e+00, 1.32513225e+00, 1.08202422e+00],
[ 1.33178377e+00, 1.32513225e+00, 1.08202422e+00],
[ 1.33178377e+00, 1.32513225e+00, 1.08202422e+00],
[ 1.33178377e+00, 1.32513225e+00, 1.08202422e+00]]), Tensor(shape=[3], dtype=Float32, value= [ 1.33178377e+00, 1.32513225e+00, 1.08202422e+00]))
(Tensor(shape=[5, 3], dtype=Float32, value=
[[ 3.31783742e-01, 3.25132251e-01, 8.20241794e-02],
[ 3.31783742e-01, 3.25132251e-01, 8.20241794e-02],
[ 3.31783742e-01, 3.25132251e-01, 8.20241794e-02],
[ 3.31783742e-01, 3.25132251e-01, 8.20241794e-02],
[ 3.31783742e-01, 3.25132251e-01, 8.20241794e-02]]), Tensor(shape=[3], dtype=Float32, value= [ 3.31783742e-01, 3.25132251e-01, 8.20241794e-02])) Auxiliary data
“Auxiliary data”,即辅助数据,指的是函数除首个输出项之外的其他输出内容。通常情况下,我们会把函数的损失(loss)设定为函数的第一个输出,而其余的输出则被定义为辅助数据。
在 grad 和 value_and_grad 中,提供了 has_aux 参数。当将其设置为 True 时,能够自动达成前面所提及的手动添加 stop_gradient 的功能,从而实现既能返回辅助数据,又不会对梯度的计算效果产生影响。
代码如下:
grad_fn = mindspore.grad(function_with_logits, (2, 3), has_aux=True)
grads, (z,) = grad_fn(x, y, w, b)
print(grads, z) 分析:首先定义了一个梯度计算函数 grad_fn ,它是通过 mindspore.grad 方法计算 function_with_logits 函数关于参数 (2, 3) 的梯度,并且设置了 has_aux=True 以处理辅助数据。
然后,通过 grad_fn 函数对输入的 x 、 y 、 w 、 b 进行梯度计算,得到梯度结果 grads 和辅助数据 z ,最后打印出 grads 和 z 。
运行结果:
(Tensor(shape=[5, 3], dtype=Float32, value=
[[ 5.98256774e-02, 8.93863812e-02, 2.36191273e-01],
[ 5.98256774e-02, 8.93863812e-02, 2.36191273e-01],
[ 5.98256774e-02, 8.93863812e-02, 2.36191273e-01],
[ 5.98256774e-02, 8.93863812e-02, 2.36191273e-01],
[ 5.98256774e-02, 8.93863812e-02, 2.36191273e-01]]), Tensor(shape=[3], dtype=Float32, value= [ 5.98256774e-02, 8.93863812e-02, 2.36191273e-01])) [-1.5198946 -1.0039824 0.88846767] 神经网络梯度计算
在深度学习领域,运用 MindSpore 框架来开展模型训练的操作,是一个常见且重要的工作。其中,涵盖了一系列关键步骤,包括精心设置模型的架构与参数、准确选定适宜的损失函数、清晰定义前向计算的流程以及精准计算梯度的逻辑。而最终将梯度结果成功打印输出,更是整个训练过程中不可或缺的一环。这一系列连贯且有序的操作,共同构成了深度学习模型训练中典型且通用的流程。
代码如下:
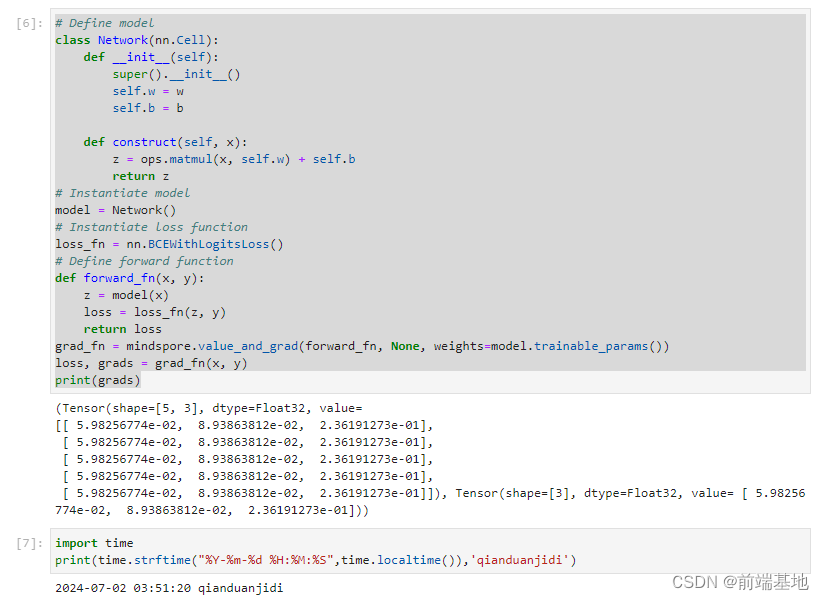
# Define model
class Network(nn.Cell):
def __init__(self):
super().__init__()
self.w = w
self.b = b
def construct(self, x):
z = ops.matmul(x, self.w) + self.b
return z
# Instantiate model
model = Network()
# Instantiate loss function
loss_fn = nn.BCEWithLogitsLoss()
# Define forward function
def forward_fn(x, y):
z = model(x)
loss = loss_fn(z, y)
return loss
grad_fn = mindspore.value_and_grad(forward_fn, None, weights=model.trainable_params())
loss, grads = grad_fn(x, y)
print(grads) 分析:class Network(nn.Cell): 定义了一个名为 Network 的类,它继承自 nn.Cell,这通常是构建神经网络模型的基础类。
def __init__(self): 这是类的初始化方法,其中 self.w = w 和 self.b = b 可能是在初始化模型的参数。
def construct(self, x): 这是模型的前向传播计算方法,通过矩阵乘法和加法计算输出 z。
model = Network(): 实例化了 Network 类,创建了一个模型对象 model。
loss_fn = nn.BCEWithLogitsLoss(): 实例化了一个二分类交叉熵损失函数 loss_fn。
def forward_fn(x, y): 定义了一个前向函数 forward_fn,它首先通过模型计算输出 z,然后使用损失函数计算损失 loss 并返回。
grad_fn = mindspore.value_and_grad(forward_fn, None, weights=model.trainable_params()): 使用 mindspore 的 value_and_grad 函数获取前向计算的损失值和关于模型可训练参数的梯度。
loss, grads = grad_fn(x, y): 调用 grad_fn 函数,并将返回的损失值和梯度分别存储在 loss 和 grads 变量中。
print(grads): 打印出计算得到的梯度值。
运行结果:
(Tensor(shape=[5, 3], dtype=Float32, value=
[[ 5.98256774e-02, 8.93863812e-02, 2.36191273e-01],
[ 5.98256774e-02, 8.93863812e-02, 2.36191273e-01],
[ 5.98256774e-02, 8.93863812e-02, 2.36191273e-01],
[ 5.98256774e-02, 8.93863812e-02, 2.36191273e-01],
[ 5.98256774e-02, 8.93863812e-02, 2.36191273e-01]]), Tensor(shape=[3], dtype=Float32, value= [ 5.98256774e-02, 8.93863812e-02, 2.36191273e-01]))