目录
1.基本概念
(1)研究案例
(2)模型框架
(3)阐述说明
(4)注意事项
2.模型的建立和求解
(1)数量级的统一
(2)归一化处理
(3)设置相应的权重
(4)科学设置权重
(5)发现问题矛盾
(6)一致性检验
(7)求解得到新的权重
3.matlab代码求解
1.基本概念
(1)研究案例

(2)模型框架
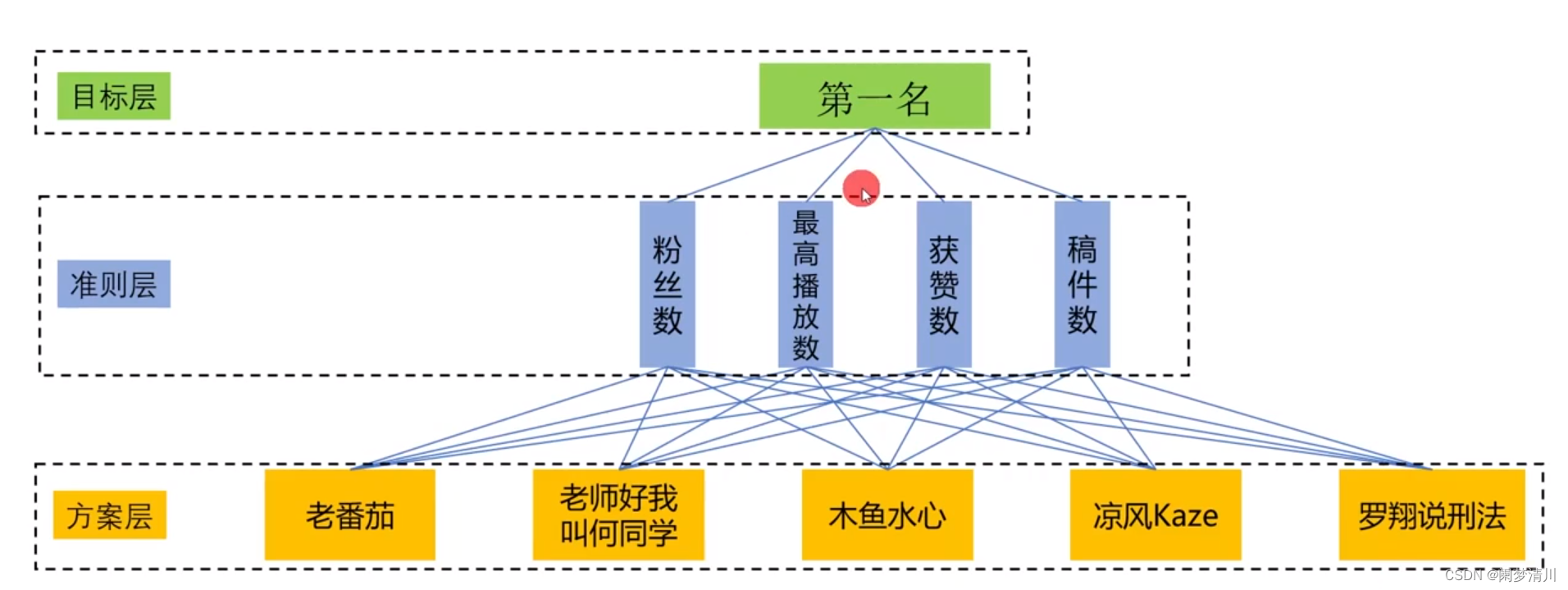
这个层次分析法适用的赛题的这个模型框架就是下面的这个,被划分为目标层,准则层,以及这个方案层,目标层就是我们想要求解的目标,准则层就是我们想要去评判的依据,方案层就是所有的可能的方案和结果;
例如对上面的这个up主的评价排名里面,我们可以使用这个粉丝数量,视频的播放量,点赞的数量和这个稿件的数量作为评判的标准;
方案层就是所有的可能结果,对于上面的这五个up主,每一个up主都是有可能作为这个第一名的,因此这个方案层里面就有五种可能的结果;
(3)阐述说明
我们要规范这个数量级以及这个权重的问题,权重显示的就是这个评判标准的重要性,下面的这个是拿罗翔老师作为一个例子的,这个罗翔老师的稿件的数量和视频的播放量不在一个数量级上面,因此这两个数据进行这个比较,运算都是没有意义的,我们到时候要在不改变这个单项排名的情况下进行归一化处理,让这两个都处于同一个数量级上面;

(4)注意事项
这个层次分析法既有缺点,也有优点,缺点就是这个层次分析法不同的这个评价标准的权重都是我们自己认为设定的,这个就会具有很强的主观性;
优点就是,即使面对复杂的问题,层次分析法依然可以提供便捷的解决方案;

2.模型的建立和求解
(1)数量级的统一
我们只看这个粉丝的数量,这个罗翔老师的粉丝的数量是最多的,我们进行相关的处理之后需要保证这个罗翔老师的粉丝的数量仍旧是第一名;
(2)归一化处理
就是按这个对应的数值除以这一列相关数值的相加求和,得到的就是这个归一化处理之后的结果,这个结果就表示对应的新排名,但是这个过程里面可能会出现问题,因为这个过程中数据的运算会涉及到四舍五入,例如这个up里面的第三个和第四个,两个人的粉丝的数量是相差了13万的,但是进行归一化处理之后这个结果却是一样的,这个就是一个缺陷,但是如果我们想要把这个差距显示出来,我们就可以提高这个精度,这样这个归一化处理之后的结果就不是一样了,但是这个差距还是很小的;
(3)设置相应的权重
我们知道,这个粉丝的数量比这个稿件的数量更能去体现这个up主的个人能力,我们肯定不能让这个归一化处理之后的结果简单的相加,而是自行的根据这个指标的重要性设置权重,得到新的结果;
(4)科学设置权重
我们上面也已经介绍了这个权重人为设置就会具有一定的主观性,因此我们需要通过科学的手段去计算权重,这个就需要使用到判断矩阵;这个规则其实也是根据人们的这个经验制定的,矩阵里面的每一个位置的数据,含义就是一个因素相较于另外一个因素的重要性,例如这个我们觉得粉丝数量比稿件的数量明显重要,我们就在以粉丝数量作为横坐标,以稿件的数量作为纵坐标的位置填写上数字5,在关于这个矩阵的主对角线的对称位置我们就是填写的他的倒数,也就是说我们只需要填写这个一个比另外一个重要的情况,反之对应的是使用的这个数据的倒数,在这个比较矩阵上面,主对角线上面的元素都是1,因为这个自己和自己进行比较,这个重要性就是一样的,所以是1
按照这个规则,我们把这个比较矩阵补充完整:
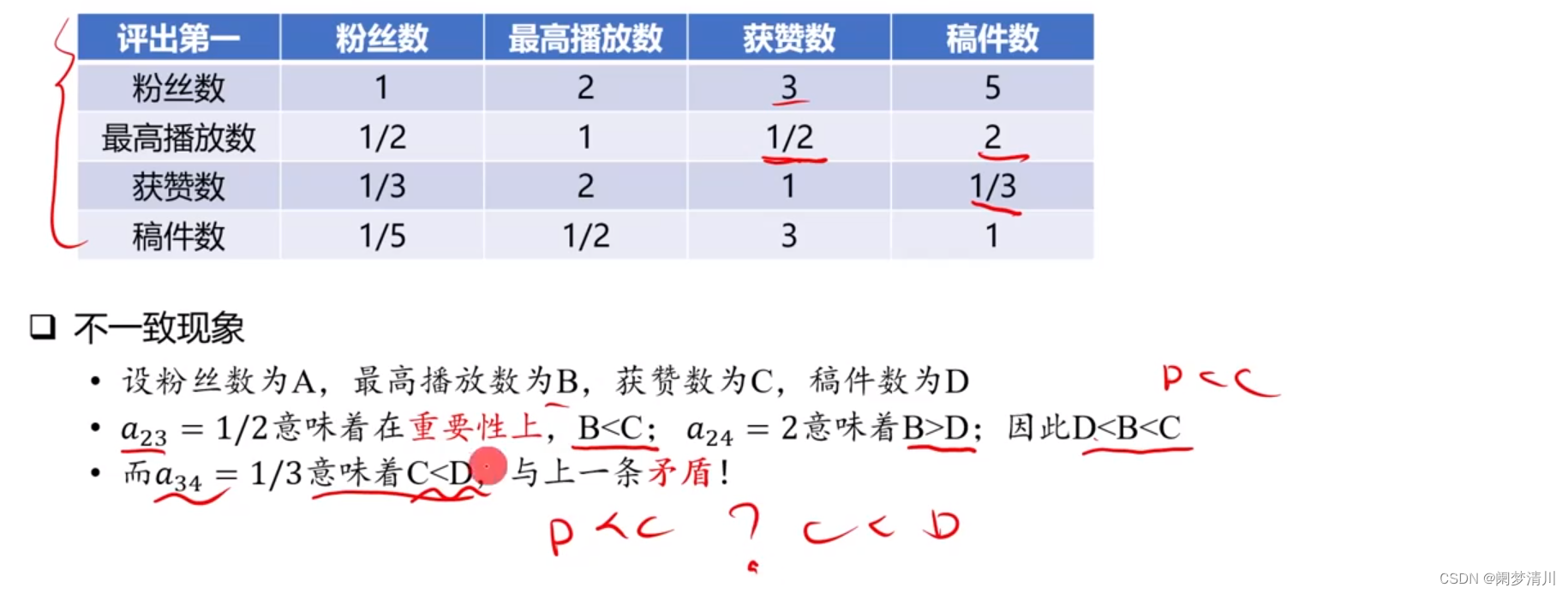
(5)发现问题矛盾
出现问题的原因就是,我们在考虑两个判断标准之间的这个重要性的时候,完全忽略了其他的指标的影响,这个时候我们再去纵览全局,就可能会发现部分的这个数据是矛盾的;

我们上面这个介绍了什么是一致矩阵,这个时候我们需要根据这个矩阵的数据元素进行一致性检验,这个矩阵的作用就是求解最大特征值,带入计算这个一致性比例,看一看是否通过检验,不符合的话需要进行这个数据的修改,重新进行一致性检验;
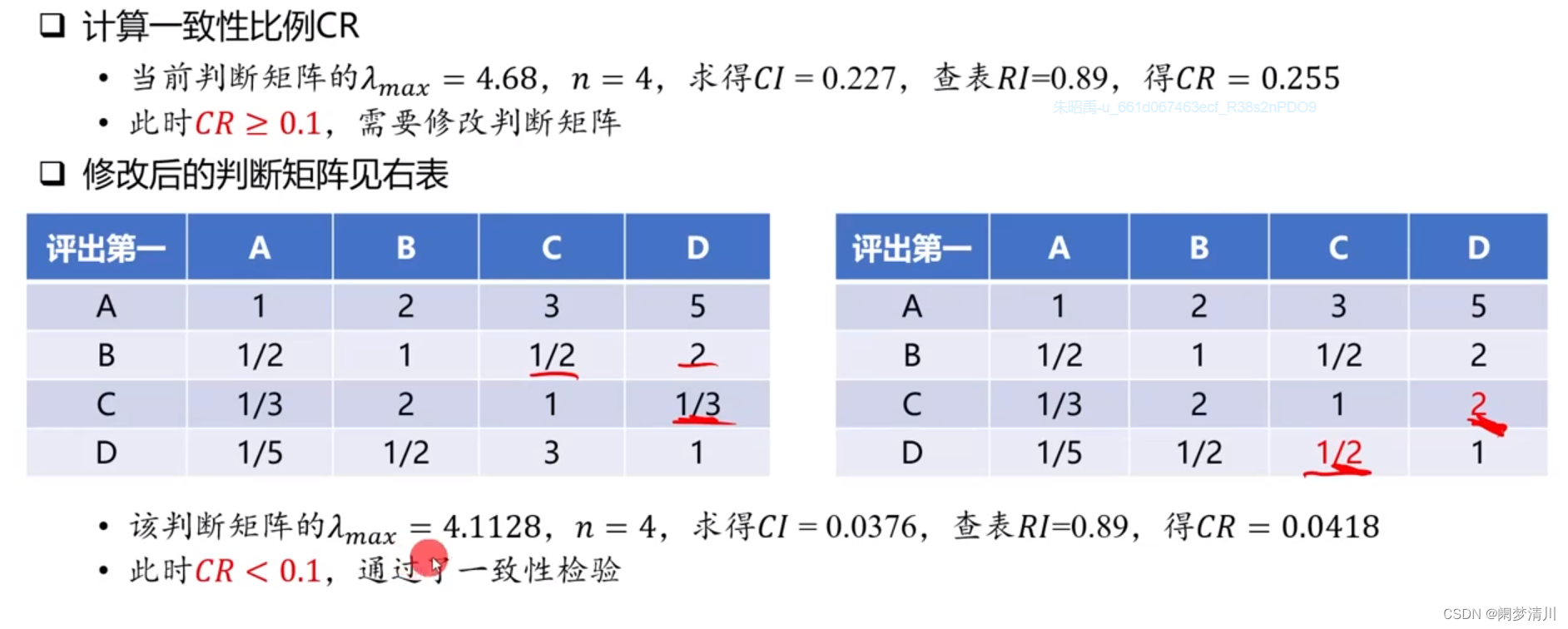
(6)一致性检验
n和RI关系的表格也是网络上面的数据,我们需要使用的时候直接查表就可以了;

修改的时候,因为我们修改一个数据之后,这个位置对应的关于对角线对称未知的元素也是会受到影响的,因此我们要修改就需要一次性修改两个数据;
(7)求解得到新的权重
通过一致性检验得到新的矩阵,案列进行归一化,再按照行得到新的权重:

这个就是新的权重,左边的数据就是我们上面进行这个数量级的统一之后得到的数据:

上面的这个过程可能会有一些繁琐,我下面放了一张图,方便大家理解:

3.matlab代码求解
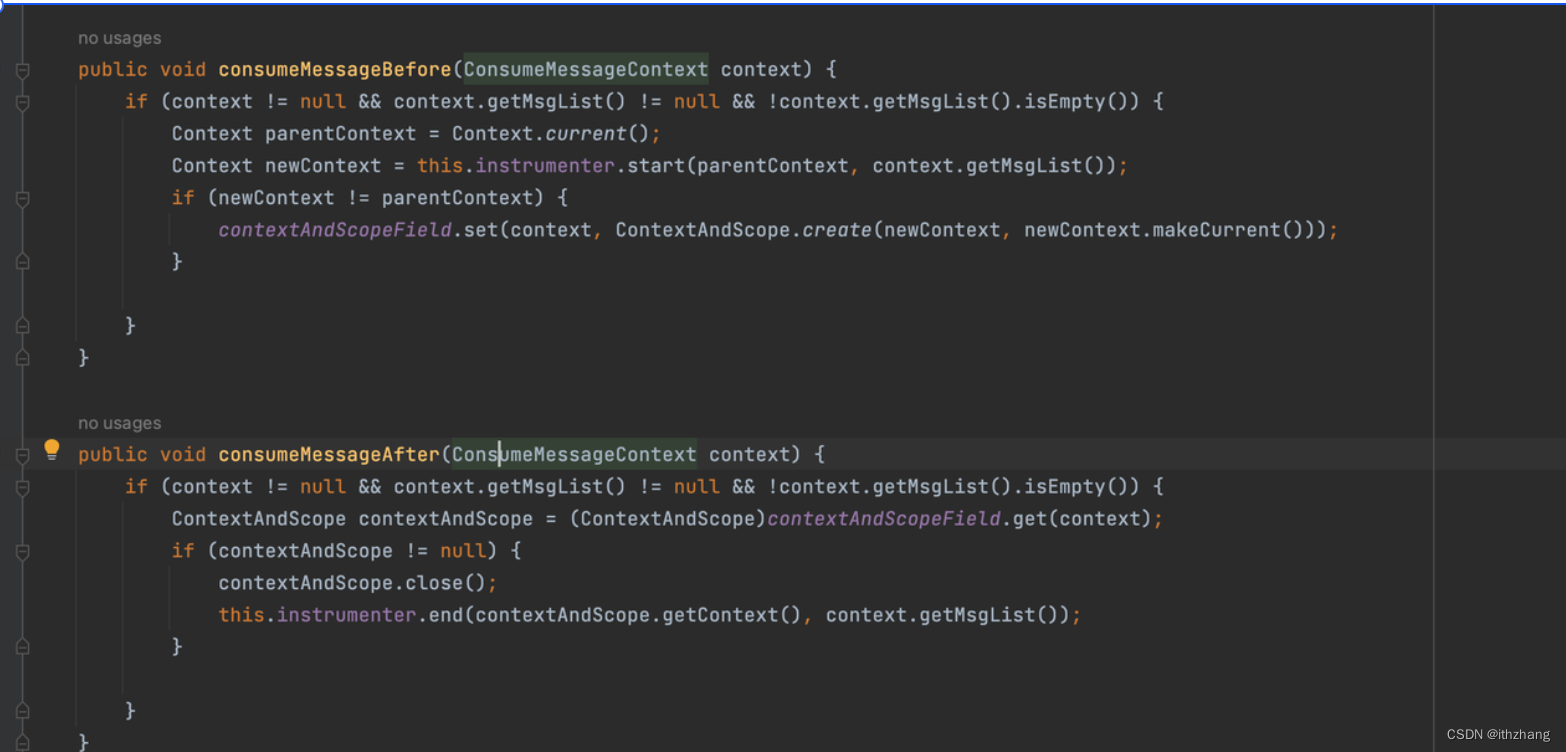
(1)上面我们介绍的进行这个一致性检验的时候,需要求借这个判断矩阵的最大特征值,再matlab里面有一个函数可以帮助我们直接进行求解,没有学过线性代数的小伙伴们也不要紧;
(2)这个判断矩阵就是我们进行这个一致性检验之后得到的这个矩阵,看上去这个代码是要进行一致性检验,实际上这个进行一致性检验之前,我们这个矩阵肯定是符合要求的,这么做只是为了让这个过程更加严谨;

(3)下面这个进行的是求解权重,先是按照列求和,再去求解每一行的平均值:

(4)把原始的数据在单位统一的情况下带入,在进行这个归一化处理,确保这个矩阵里面的元素的单位是一样的,这个归一化处理就是得到这个新的比例;
带入的就是下面的这个数据:


(5)相信你也看到了,这个过程并不是很简单,下面我趁着自己刚刚做完,简单的梳理一下,这个matlab里面的这个操作的步骤:
先是在原来的表格上面搞判断矩阵,谁相对于谁的重要程度,再去根据这个一致性检验的公式运算,符合一致性检验之后,按照列求和,算出这一列的每一列数据在这一列的权重,在按照行求解平均值,得到权重(科学的,相对客观的);
在带入这个最原始的数据,在单位统一的情况下还是求解数据在这一列的权重,在按照行求解平均值,让这个向量和权重向量做乘法,得到最后的评分;
(6)matlab代码
clc,clear
% 输入判断矩阵
A = [1 2 3 5
1/2 1 1/2 2
1/3 2 1 2
1/5 1/2 1/2 1];
% eig求出矩阵特征值。max求最大值
maxlam = max(eig(A))
[~,n]=size(A) % 评价指标个数,就是A的行数。A是方阵,行数列数一样
RI=[0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45];
CI=(maxlam-n)/(n-1)
CR=CI/RI(n)
if CR<0.10 %如果误差小于0.1则可以接受
disp('该矩阵通过一致性检验。');
else
disp('该矩阵未通过一致性检验!');
return % 终止运行
end
% 归一化处理
[n,~]=size(A); % 判断矩阵A是方阵,返回行数n即评价指标个数
Asum=sum(A,1); % 按列求和
Aprogress=A./(ones(n,1)*Asum);
%每一行分别求和,求和的结果除以𝑛,得到的列向量就是权重向量
W=sum(Aprogress,2)./n;
% 输入原始数据
% 注意,要确保同一列的数据单位相同!!!
data = [1686.4 3183 12000 397
903.6 1916.4 3439.6 43
837.6 817.6 4748 1159
824.9 1296.4 12000 442
2110.2 1465.7 6199.5 228];
% 归一化处理
[mm,nn]=size(data); % 数据行数和列数
for j=1:nn % 针对每一列
msum=sum(data(:,j)); % 求这一列元素之和
for i=1:mm % 针对每一行
data(i,j)=data(i,j)./msum; % 每个元素的值都除以所在列的元素之和
end
end
% 数据矩阵乘以权重列向量
% 也就是综合评分=0.49粉丝数+0.18播放数+0.23获赞数+0.1稿件数
grade = data*W