数据结构 —— 图的表示
- 图的基本概念
- 图的表示
今天我们来看看一个较为复杂的数据结构:图:
图的基本概念
在计算机科学中,“图”(Graph)是一种重要的非线性数据结构,用于表示对象集合及对象之间的多种关系。它由顶点(Vertex)和边(Edge)组成,能够有效地模拟和解决许多现实世界的问题,如网络路由、任务调度、社交网络分析等。下面是计算机中图概念的几个关键点:
- 定义:图
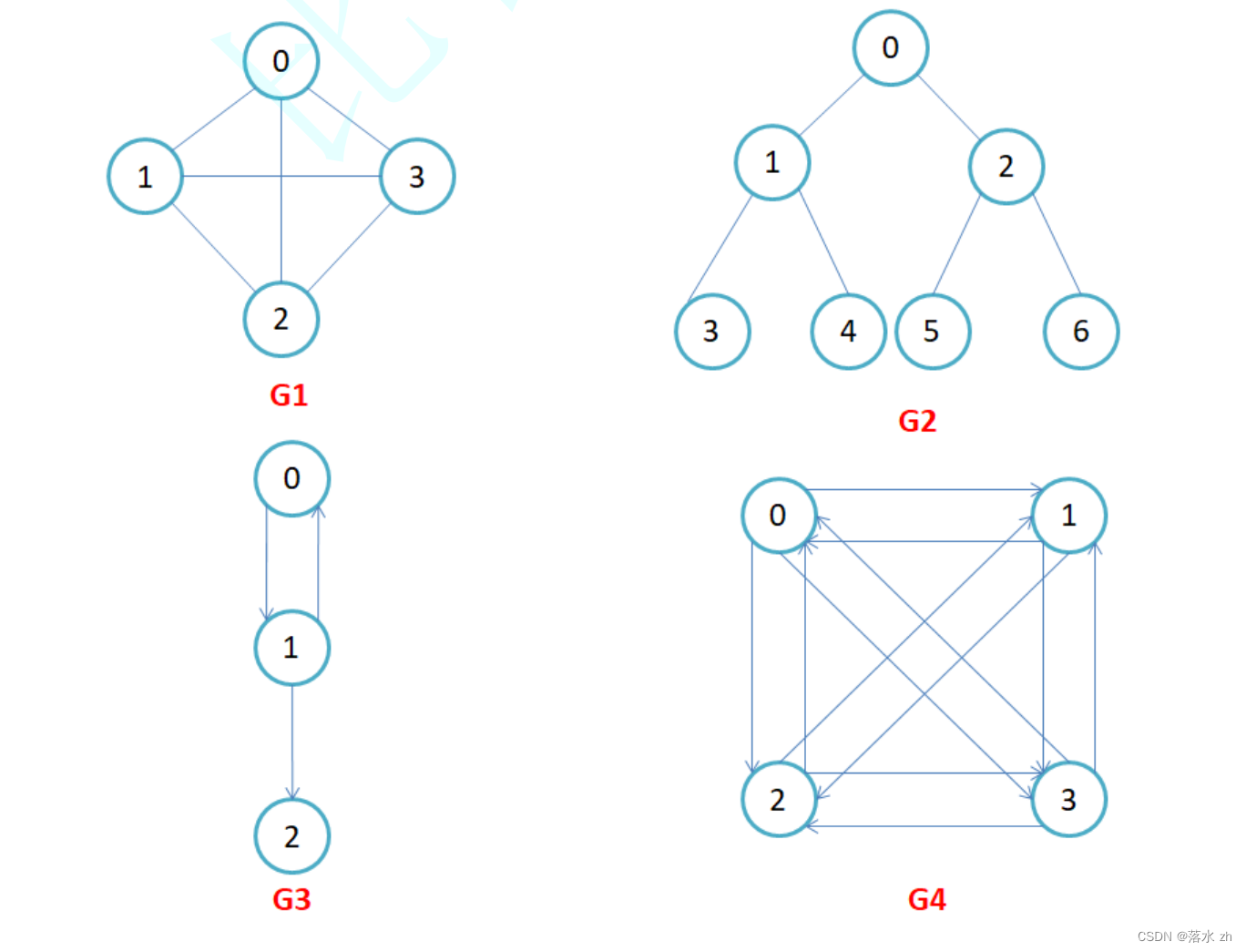
G=(V,E)由两个主要部分构成:顶点集V和边集E。顶点代表图中的实体或对象,边则表示顶点间的某种关系。顶点集V(G)和边集E(G)分别表示图G的顶点集合和边集合。
- 无向图与有向图:
- 无向图:图中的边没有方向,表示顶点间的对称关系。如果顶点
u和顶点v之间有一条边,则从u到v和从v到u的关系是相同的。- 有向图:图中的边具有方向,表示从一个顶点到另一个顶点的单向关系。一条从顶点
u指向顶点v的边表示一种特定方向的关系。
- 完全图:在一个有
n个顶点的图中,如果每一对不同的顶点之间都恰好有一条边相连,则这个图被称为完全图。无向完全图有n(n-1)/2条边,有向完全图有n(n-1)条边。
- 带权图:图中的边可以被赋予一个数值,称为权重(Weight),这可以代表距离、成本、时间或其他任何度量。带权图在解决诸如最短路径问题时特别有用。
- 应用:图在计算机科学中有广泛的应用,包括但不限于:
- 路径查找:如Dijkstra算法、A*算法用于寻找两点间的最短路径。
- 网络流:如最大流/最小割问题,应用在网络设计、资源分配等领域。
- 图的遍历:深度优先搜索(DFS)、广度优先搜索(BFS)用于访问图中所有顶点。
- 图的连通性:检测图是否连通,计算连通分量等。
- 社交网络分析:发现社群结构、影响力分析等。
- 推荐系统:基于用户或物品间的关系构建推荐模型。
图作为数据结构的灵活性和表达能力使其成为理解和解决复杂问题的强大工具。
图的表示
我们了解了图的概念,现在有一个问题,我们应该如何表示图呢,我们一般有两种方式:
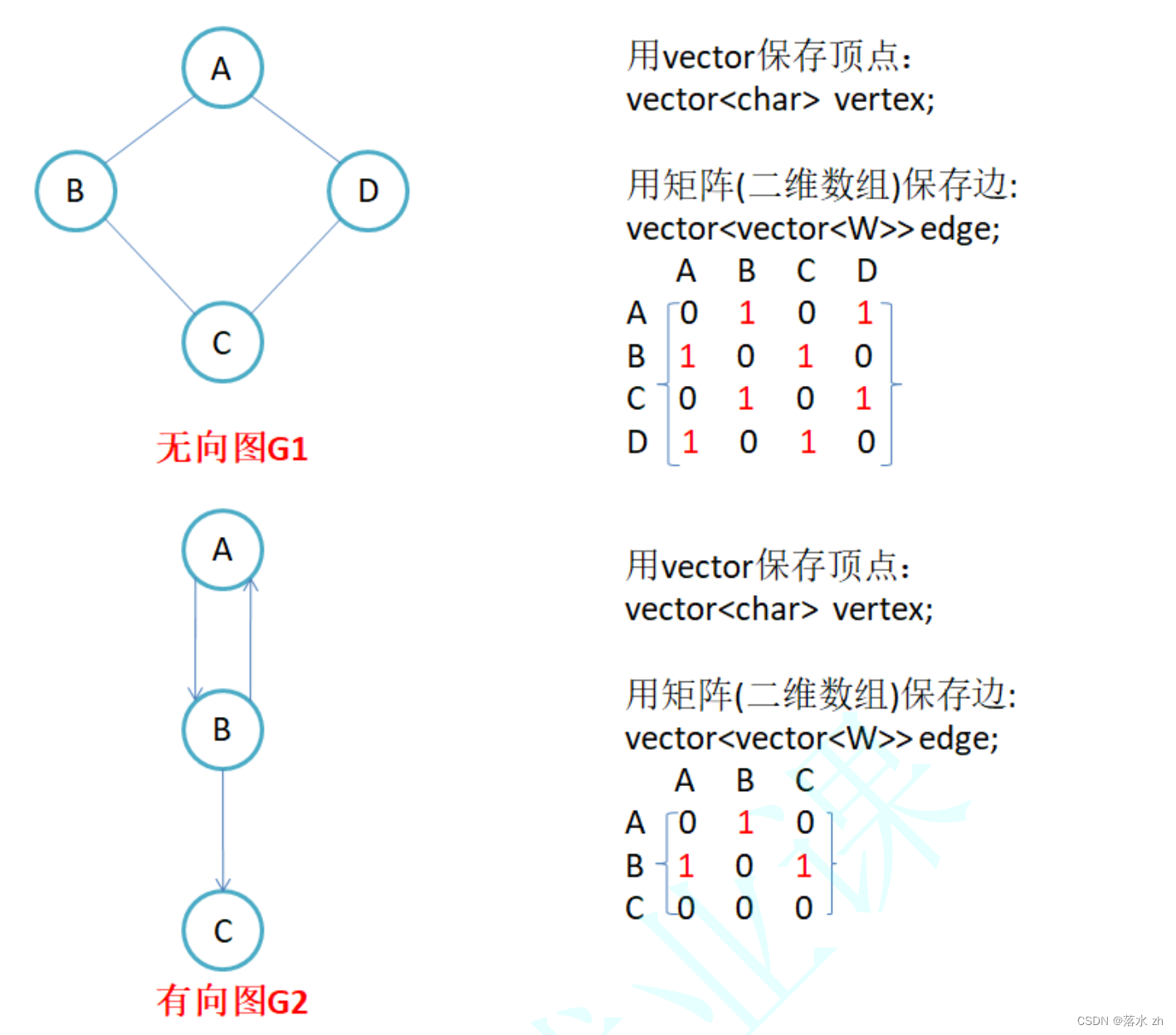
图的表示方法主要有两种:邻接矩阵和邻接表。
- 邻接矩阵:
邻接矩阵是一种使用二维数组来表示图中顶点之间关系的方法。对于一个有n个顶点的图,我们可以创建一个n×n的矩阵A,矩阵中的元素A[i][j]表示图中第i个顶点到第j个顶点是否存在边。如果存在边,则A[i][j]=1(对于无权图)或A[i][j]=权重值(对于有权图);如果不存在边,则A[i][j]=0。邻接矩阵的优点是直观且易于实现图的遍历,但空间消耗较大,特别是当图稀疏时(边的数量远小于顶点数量的平方)。
namespace martix
{
// 定义一个图类模板,参数为顶点类型V,边权重类型W,最大权重值MAX_W,以及是否是有向图Direction
template<class V,class W,
W MAX_W,bool Direction = false>
class Graph
{
public:
// 构造函数,初始化邻接矩阵,接受顶点数组和顶点数量
Graph(const V* vertexs, int n)
{
// 为顶点容器预留空间以提高效率
_vertexs.reserve(n);
// 遍历顶点数组,将每个顶点添加到_vertexs,并记录其索引到_index映射中
for(int i = 0; i < n; i++)
{
_vertexs.push_back(vertexs[i]);
_index[vertexs[i]] = i;
}
// 初始化邻接矩阵,大小为n*n,初始值为MAX_W表示无连接
_martix.resize(n);
for(auto &row : _martix)
{
row.resize(n, MAX_W);
}
}
// 获取顶点的索引
int GetVertexIndex(const V& v)
{
// 查找顶点在_index中的映射,存在则返回索引,否则抛出异常
auto ret = _index.find(v);
if(ret != _index.end())
{
return ret->second;
}
else
{
throw std::invalid_argument("不存在的顶点");
return -1; // 实际不会执行到此行,因为已抛出异常
}
}
// 内部使用的加边函数,根据源顶点和目标顶点索引以及权重添加边
void _AddEdge(int srci, int desi, const W& w)
{
_martix[srci][desi] = w; // 设置边的权重
// 如果图是非定向的,则对称地添加边
if(Direction == false)
{
_martix[desi][srci] = w;
}
}
// 公开的加边接口,通过顶点名称和权重调用内部加边函数
void AddEdge(const V& srci, const V& desi, const W& w)
{
int src = GetVertexIndex(srci); // 获取源顶点索引
int des = GetVertexIndex(desi); // 获取目标顶点索引
_AddEdge(src, des, w); // 调用内部函数添加边
}
// 打印图的邻接矩阵表示
void Print()
{
// 先打印顶点标签
std::cout << " ";
for(size_t i = 0; i < _vertexs.size(); i++)
{
std::cout << _vertexs[i] << " ";
}
std::cout << std::endl;
// 遍历并打印邻接矩阵,MAX_W的位置用#代替
for(int i = 0; i < _vertexs.size(); i++)
{
std::cout << i << " ";
for(int j = 0; j < _vertexs.size(); j++)
{
if(_martix[i][j] != MAX_W)
std::cout << _martix[i][j] << " ";
else
std::cout << "# ";
}
std::cout << std::endl;
}
}
private:
// 存储图的顶点
std::vector<V> _vertexs;
// 顶点到其在_vector中的索引的映射
std::map<V,int> _index;
// 邻接矩阵表示的图
std::vector<std::vector<W>> _martix;
};
// 测试函数,创建并操作一个有向图实例
void TestGraph1()
{
// 使用字符作为顶点标识,整数作为边权重,INT_MAX表示无边,图是有向的
Graph<char, int, INT_MAX, true> g("0123", 4);
// 添加边及其权重
g.AddEdge('0', '1', 1);
g.AddEdge('0', '3', 4);
g.AddEdge('1', '3', 2);
g.AddEdge('1', '2', 9);
g.AddEdge('2', '3', 8);
g.AddEdge('2', '1', 5);
g.AddEdge('2', '0', 3);
g.AddEdge('3', '2', 6);
// 打印图
g.Print();
}
}

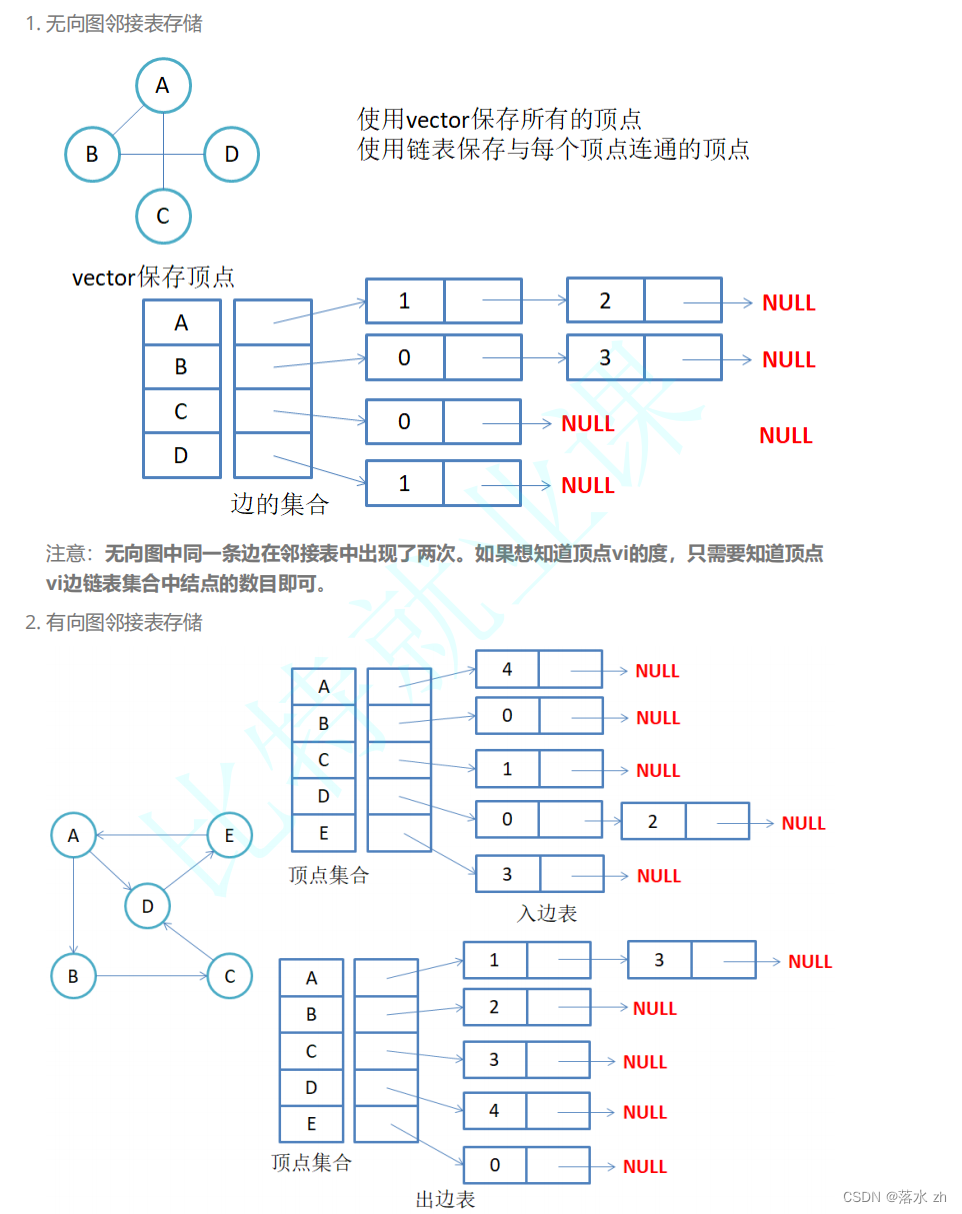
- 邻接表:
邻接表是另一种常用的图表示法,特别适合于表示稀疏图。它由一个顶点列表和一系列的边列表(链表)组成。顶点列表存储图中所有的顶点,而每个顶点对应一个链表,这个链表包含了所有与该顶点直接相连的其他顶点(邻居)。链表中的每个节点通常包含两个信息:指向邻居顶点的指针和边的权重(对于有权图)。邻接表的优点是节省空间,特别是在图稀疏的情况下,但访问特定边可能不如邻接矩阵直接。
namespace link_table
{
// 定义边的结构体,包含目的顶点索引、权值和指向下一个边的指针
template<class W>
struct Edge
{
int _desIndex; // 目的顶点索引
W _w; // 边的权值
Edge<W>* _next; // 指向下一个边的指针
// 构造函数,初始化边的基本信息
Edge(int desIndex, const W& w)
: _desIndex(desIndex), _w(w), _next(nullptr) {}
};
// 图类模板,采用邻接表表示图
template<class V,class W,bool Direction = false>
class Graph
{
public:
// 类型定义,简化Edge类型的引用
typedef Edge<W> Edge;
// 构造函数,初始化顶点信息和邻接表
Graph(const V* vertexs, size_t n)
{
_vertexs.reserve(n); // 为顶点容器预留空间
// 遍历顶点数组,添加顶点到_vertexs,并建立顶点到索引的映射
for(size_t i = 0; i < n; i++)
{
_vertexs.push_back(vertexs[i]);
_index[vertexs[i]] = i;
}
// 初始化邻接表,每个顶点对应的链表头指针初始化为空
_martix.resize(n, nullptr);
}
// 获取顶点索引
size_t GetVertexIndex(const V& v)
{
auto ret = _index.find(v);
// 如果找到顶点,则返回其索引,否则抛出异常
if(ret != _index.end())
{
return ret->second;
}
else
{
throw std::invalid_argument("不存在的顶点");
return -1; // 实际不会执行到此行,因为已抛出异常
}
}
// 添加边,根据顶点名称和权值在图中添加边
void AddEdge(const V& src, const V& des, W w)
{
size_t srcIndex = GetVertexIndex(src);
size_t desIndex = GetVertexIndex(des);
// 创建新边,并将其插入源顶点的链表头部
Edge* edge = new Edge(desIndex, w);
edge->_next = _martix[srcIndex];
_martix[srcIndex] = edge;
// 若图无向,则对称地在目标顶点链表中也插入边
if(Direction == false)
{
Edge* edgeRev = new Edge(srcIndex, w);
edgeRev->_next = _martix[desIndex];
_martix[desIndex] = edgeRev;
}
}
// 打印图的邻接表表示
void Print()
{
// 遍历每个顶点,打印其邻接链表
for(size_t i = 0; i < _vertexs.size(); i++)
{
std::cout << _vertexs[i] << "[" << i << "]:";
Edge* cur = _martix[i]; // 当前顶点的链表头指针
while(cur)
{
// 打印目的顶点索引和权值,以及指向下一个边的箭头
std::cout << _vertexs[cur->_desIndex] << "[" << cur->_desIndex << "]"
<< cur->_w << "->";
cur = cur->_next; // 移动到链表的下一个节点
}
std::cout << "nullptr" << std::endl; // 链表结束标记
}
}
private:
// 存储图的顶点
std::vector<V> _vertexs;
// 顶点到索引的映射
std::map<V,int> _index;
// 邻接表,每个元素是一个指向边的指针
std::vector<Edge*> _martix;
};
// 测试函数,创建并操作一个无向图实例
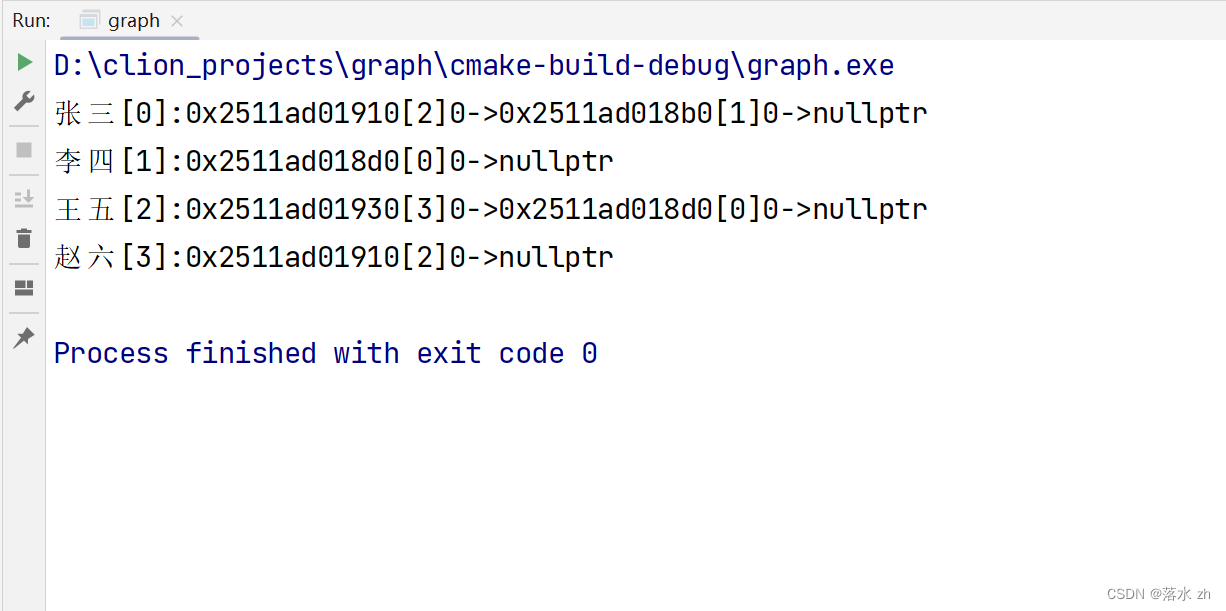
void TestGraph1()
{
std::string a[] = { "张三", "李四", "王五", "赵六" };
// 创建图实例,并添加边
Graph<std::string, int> g1(a, 4);
g1.AddEdge("张三", "李四", 100);
g1.AddEdge("张三", "王五", 200);
g1.AddEdge("王五", "赵六", 30);
// 打印图
g1.Print();
}
}